accelerare instantanee Este schimbarea pe care o experimentează viteza pe unitate de timp în fiecare moment al mișcării. În momentul precis când „dragster”Dintre imagini a fost fotografiată, a avut o accelerație de 29,4 m / sDouă. Aceasta înseamnă că, în acel moment, viteza sa era crescută cu 29,4 m / s în intervalul de 1 s. Acest lucru este echivalent cu 105 km / h în doar 1 secundă.
O competiție de dragster este ușor de modelat presupunând că mașina de curse este un obiect punctat. P care se mișcă în linie dreaptă. Pe această linie se alege o axă orientată cu originea SAU că vom numi axaBOU) sau doar ax X.
Variabilele cinematice care definesc și descriu mișcarea sunt:
Toate sunt cantități vectoriale. Prin urmare, ei au o magnitudine, o direcție și un simț.
În cazul mișcării rectilinii există doar două direcții posibile: pozitivă (+) în direcția (BOU) sau negativ (-) în direcția opusă lui (BOU). Prin urmare, este posibil să renunțați la notația formală vectorială și să folosiți semnele pentru a indica sensul mărimii.
Indice articol
Să presupunem că în acest moment t particula are viteză v (t) și în clipa aceea nu viteza sa este v (t ').
Deci schimbarea pe care a avut-o viteza în acea perioadă de timp a fost Δv = v (t ') - v (t). De aici accelerarea în intervalul de timp Δt = t '- t , ar fi dat de coeficientul:
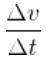
Acest coeficient este accelerarea medie lam în perioada de timp Δt dintre instanțele t și t '.
Dacă am fi vrut să calculăm accelerația exact la momentul t, atunci t 'ar trebui să fie o cantitate nesemnificativ mai mare decât t. Cu acest Δt, care este diferența dintre cele două, ar trebui să fie aproape zero.
Matematic se indică după cum urmează: Δt → 0 și se obține:
Eu) O particulă se mișcă de-a lungul axei X cu viteza constantă v0 = 3 m / s. Care va fi accelerarea particulei?
Derivata unei constante este zero, prin urmare accelerația unei particule care se deplasează cu viteză constantă este zero.
II) O particulă se mișcă pe axă X iar viteza sa se schimbă în timp conform următoarei formule:
v (t) = 2 - 3t
Unde viteza este măsurată în m / s și timpul în s. Care va fi accelerarea particulei?
)
Rezultatul este interpretat astfel: pentru orice moment accelerația este de -3 m / s.
Între momentele 0 s și 2/3 s viteza este pozitivă în timp ce accelerația este negativă, adică în acel interval particula își micșorează viteza sau decelerează.
În momentul 2/3 s, viteza sa devine zero, dar pe măsură ce rămâne o accelerație de -3 m / s, din acel moment viteza se inversează (devine negativă).
În momentele după ⅔ s, particula accelerează, deoarece de fiecare dată viteza sa devine mai negativă, adică viteza sa (modulul de viteză) crește.
III) Figura arată o curbă care reprezintă viteza în funcție de timp, pentru o particulă care se deplasează de-a lungul axei X. Găsiți semnul accelerației la momente t1, tDouă si tu3. De asemenea, indicați dacă particula accelerează sau decelerează.
Accelerația este derivata funcției vitezei, prin urmare este echivalentă cu panta liniei tangente la curba v (t) pentru un moment dat t.
Pentru momentul t1, panta este negativă, deci accelerația este negativă. Și întrucât în acel moment viteza este pozitivă, putem afirma că în acel moment particula decelerează.
Pentru momentul tDouă linia tangentă la curba v (t) este orizontală, deci panta sa este zero. Mobilul are o accelerație zero, deci la tDouă particula nici nu accelerează, nici nu decelerează.
Pentru momentul t3, panta liniei tangente la curba v (t) este pozitivă. Cu o accelerație pozitivă, particula accelerează într-adevăr, deoarece în acel moment viteza este, de asemenea, pozitivă.
În secțiunea anterioară, accelerația instantanee a fost definită de la viteza instantanee. Cu alte cuvinte, dacă viteza este cunoscută în fiecare moment, atunci este, de asemenea, posibil să se cunoască accelerația în fiecare moment al mișcării..
Procesul invers este posibil. Adică, cunoscând accelerația pentru fiecare moment, atunci viteza instantanee poate fi calculată.
Dacă operația care permite trecerea de la viteză la accelerație este derivată, operația matematică opusă este integrarea.
Accelerația unei particule care se mișcă de-a lungul axei X este a (t) = ¼ tDouă. Unde t se măsoară în secunde și a în m / s. Determinați accelerația și viteza particulei la 2 s de mișcare, știind că la momentul inițial t0 = 0 era în repaus.
La 2 s accelerația este de 1 m / sDouă iar viteza pentru instant t va fi dată de:
Un obiect se deplasează de-a lungul axei X cu o viteză în m / s, dată de:
v (t) = 3 tDouă - 2 t, unde t se măsoară în secunde. Determinați accelerația la momente: 0s, 1s, 3s.
Luând derivata lui v (t) față de t, se obține accelerația în orice moment:
a (t) = 6t -2
Apoi a (0) = -2 m / sDouă ; a (1) = 4 m / sDouă ; a (3) = 16 m / sDouă .
O sferă metalică este eliberată din partea de sus a unei clădiri. Accelerația în scădere este accelerația gravitației care poate fi aproximată cu valoarea 10 m / s2 și îndreptată în jos. Determinați viteza sferei 3 s după ce a fost eliberată.
Această problemă implică accelerarea gravitației. Luând direcția verticală ca pozitivă jos, avem că accelerația sferei este:
a (t) = 10 m / sDouă
Iar viteza va fi dată de:
O sferă metalică este împușcată în sus cu o viteză inițială de 30 m / s. Accelerația mișcării este accelerația gravitației care poate fi aproximată cu valoarea 10 m / sDouă și arătând în jos. Determinați viteza sferei la 2 s și 4 s după ce a fost împușcată.
Direcția verticală va fi luată ca pozitivă în sus. ȘIÎn acest caz, accelerația mișcării va fi dată de
a (t) = -10 m / sDouă
Viteza în funcție de timp va fi dată de:
După 4 s de tragere, viteza va fi de 30 - 10 ∙ 4 = -10 m / s. Ceea ce înseamnă că la 4 s sfera coboară cu o viteză de 10 m / s.
Nimeni nu a comentat acest articol încă.