
Măsură de arc (geometrie), tipuri de arcuri, exemple
arc, în geometrie, este orice linie curbată care leagă două puncte. O linie curbă, spre deosebire de o linie dreaptă, este una a cărei direcție este diferită la fiecare punct de pe ea. Opusul unui arc este un segment, deoarece aceasta este o secțiune dreaptă care unește două puncte.
Arcul cel mai frecvent utilizat în geometrie este arcul de circumferință. Alte arcade de uz comun sunt arc parabolic, arc eliptic și arc catenar. Forma arcului este, de asemenea, frecvent utilizată în arhitectură ca element decorativ și ca element structural. Acesta este cazul buiandrugurilor ușilor și ferestrelor, precum și ale podurilor și apeductelor.

Indice articol
- 1 Arcul și măsura sa
- 2 Tipuri de arcuri
- 2.1 Arcul circular
- 2.2 Arcul parabolic
- 2.3 Arcul catenar
- 2.4 Arcul eliptic
- 3 Exemple de arcade
- 3.1 Exemplul 1
- 3.2 Exemplul 2
- 4 Referințe
Arcul și măsura lui
Măsura unui arc este lungimea acestuia, care depinde de tipul de curbă care leagă cele două puncte și de locația lor..
Lungimea unui arc de cerc este una dintre cele mai simple de calculat, deoarece se cunoaște lungimea arcului complet sau a perimetrului unei circumferințe.
Perimetrul unui cerc este de două pi ori de radio: p = 2 π R. Știind acest lucru, dacă doriți să calculați lungimea s a unui arc circular de unghi α (măsurat în radiani) și raza R, se aplică un raport:
(s / p) = (α / 2 π)
Apoi curățare s din expresia anterioară și înlocuind perimetrul p prin expresia sa în funcție de rază R, aveți:
s = (α / 2 π) p = (α / 2 π) (2 π R) = α R.
Adică, măsura unui arc circular este produsul deschiderii sale unghiulare de raza arcului circular.
Pentru un arc în general, problema este mai complicată, până la punctul în care marii gânditori ai antichității au afirmat că este o sarcină imposibilă..
Abia la apariția calculului diferențial și integral în 1665, problema măsurării oricărui arc a fost rezolvată în mod satisfăcător.
Înainte de invenția calculului diferențial, soluțiile puteau fi găsite numai folosind linii poligonale sau arcuri de circumferință care aproximau arcul adevărat, dar aceste soluții nu erau exacte.
Tipuri de arcuri
Din punct de vedere al geometriei, arcurile sunt clasificate în funcție de linia curbată care unește două puncte pe plan. Există alte clasificări în funcție de utilizare și forma arhitecturală.
Arcul circular
Când linia care leagă două puncte ale planului este o bucată de circumferință de o anumită rază, avem un arc circular. Figura 2 prezintă un arc circular circular cu raza R care leagă punctele A și B.
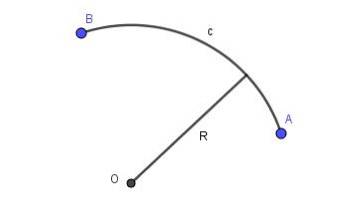
Arc parabolic
Parabola este calea urmată de un obiect care a fost aruncat oblic în aer. Când curba care unește două puncte este o parabolă, atunci avem un arc parabolic ca cel prezentat în figura 3.
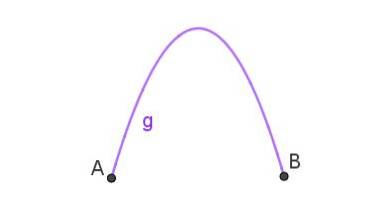
Aceasta este forma jetului de apă care iese dintr-un furtun îndreptat în sus. Arcul parabolic poate fi observat în sursele de apă.

Arc catenar
Arcul catenar este un alt arc natural. Catenaria este curba care se formează în mod natural atunci când un lanț sau o frânghie atârnă liber de două puncte separate.
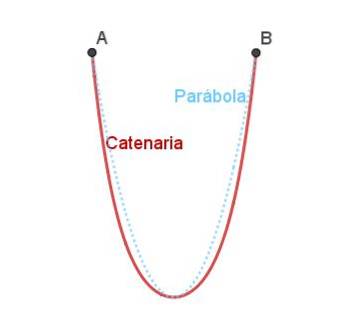
Catenaria este similară cu parabola, dar nu este exact la fel cum se poate vedea în figura 4.
Arcul catenar inversat este utilizat în arhitectură ca element structural cu rezistență mare la compresiune. De fapt, se poate demonstra că este cel mai puternic tip de arc din toate formele posibile..
Pentru a construi un arc catenar solid, trebuie doar să copiați forma unei frânghii sau a unui lanț agățat, apoi forma copiată este răsturnată pentru a o reproduce pe ușa sau pragul ferestrei.
Arcul eliptic
Un arc este eliptic dacă curba care leagă două puncte este o piesă sau o secțiune a unei elipse. Elipsa este definită ca locusul punctelor a căror distanță față de două puncte date se adaugă întotdeauna la o cantitate constantă.
Elipsa este o curbă care apare în natură: este curba traiectoriei planetelor în jurul Soarelui, așa cum a demonstrat Johannes Kepler în anul 1609.
În practică, o elipsă poate fi desenată prin fixarea a două stâlpi la sol sau a două știfturi pe hârtie și legarea unui șir de ele. Coarda este apoi tensionată cu markerul sau creionul și curba este trasată. O bucată de elipsă este un arc eliptic. Următoarea animație ilustrează modul în care este desenată elipsa:
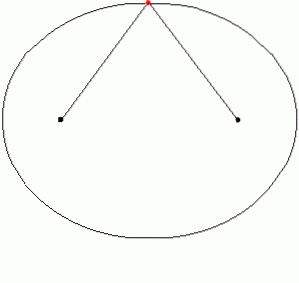
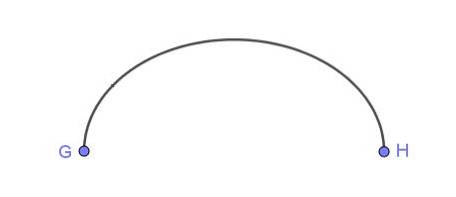
Figura 6 prezintă un arc eliptic care leagă punctele G și H.
Exemple de arcade
Următoarele exemple se referă la modul de calculare a perimetrului unor arcade specifice.
Exemplul 1
Figura 7 prezintă o fereastră finisată într-un arc circular tăiat. Dimensiunile prezentate în figură sunt în picioare. Calculați lungimea arcului.
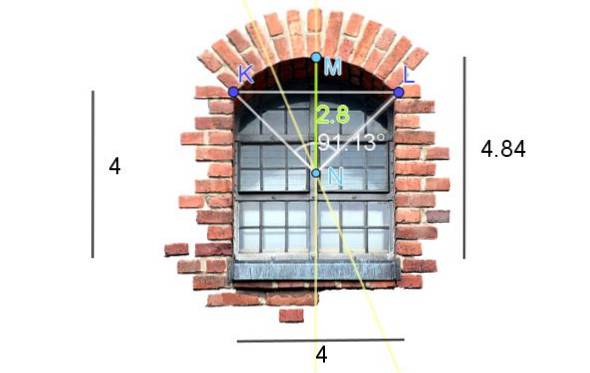
Pentru a obține centrul și raza arcului circular al buiandrugului, următoarele imagini sunt realizate:
-Segmentul KL este trasat și bisectoarea acestuia este trasată.
-Ulterior, se află cel mai înalt punct al buiandrugului, pe care îl numim M. În continuare, se ia în considerare segmentul KM și se urmărește mediatrița acestuia..
Intercepția celor două bisectoare este punctul N și este, de asemenea, centrul arcului circular.
-Acum trebuie să măsurăm lungimea segmentului NM, care coincide cu raza R a arcului circular: R = 2,8 picioare.
-Pentru a cunoaște lungimea arcului în plus față de rază, este necesar să cunoaștem unghiul pe care îl formează arcul. Care poate fi determinată prin două metode, fie se măsoară cu un raportor, fie se calculează utilizând trigonometria.
În cazul prezentat, unghiul format de arc este de 91,13º, care trebuie convertit în radiani:
91,13º = 91,13º * π / 180º = 1,59 radiani
În cele din urmă, calculăm lungimea s a arcului folosind formula s = α R.
s = 1,59 * 2,8 picioare = 4,45 picioare
Exemplul 2
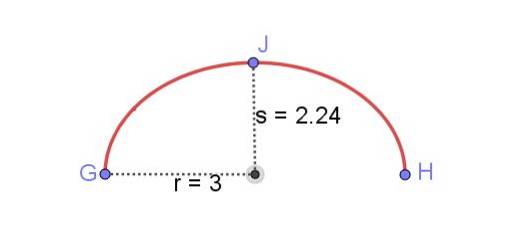
Găsiți lungimea arcului eliptic prezentat în figura 8, cunoscând axa semi-majoră r iar axa semi-minoră s a elipsei.
Găsirea lungimii unei elipse a fost una dintre cele mai dificile probleme în matematică de mult timp. Puteți obține soluții exprimate prin integrale eliptice, dar pentru a avea o valoare numerică trebuie să extindeți aceste integrale în serie de putere. Un rezultat exact ar necesita termeni infiniti ai acelor serii.
Din fericire, geniul matematic hindus Ramanujan, care a trăit între 1887 și 1920, a găsit o formulă care aproximează foarte precis perimetrul unei elipse:
Perimetrul unei elipse = π [3 (r + s) - √ ((3r + s) (r + 3s))]
Perimetrul unei elipse cu r = 3 cm și s = 2,24 cm este de 16,55 cm. Cu toate acestea, arcul eliptic prezentat are jumătate din valoare:
Lungimea arcului eliptic GH = 8,28 cm.
Referințe
- Clemens S. 2008. Geometrie și Trigonometrie. Pearson Education.
- García F. Proceduri numerice în Java. Lungimea unei elipse. Recuperat de pe: sc.ehu.es
- Geometrie dinamică. Arcuri. Recuperat de la geometriadinamica.es
- Piziadas. Elipsele și parabolele din jurul nostru. Recuperat de pe: piziadas.com
- Wikipedia. Arc (geometrie). Recuperat de pe: es.wikipedia.com



Nimeni nu a comentat acest articol încă.