Încărcare radială cum se calculează, exerciții rezolvate

sarcina radială Este forța care se exercită perpendicular pe axa de simetrie a unui obiect și a cărei linie de acțiune trece prin această axă. De exemplu, o curea pe un scripete impune o sarcină radială pe lagărul sau lagărul arborelui scripetei..

În figura 1 săgețile galbene reprezintă forțe radiale sau sarcini pe arbori datorită tensiunii curelei care trece prin scripeți.

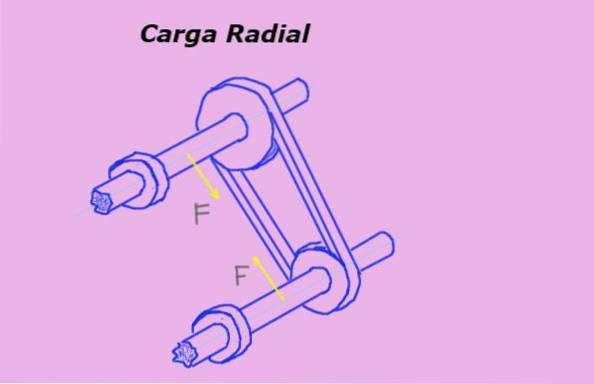
Unitatea de măsură pentru sarcina radială în sistemul internațional sau SI este Newton (N). Dar alte unități de forță sunt, de asemenea, utilizate frecvent pentru a o măsura, cum ar fi forța kilogramului (Kg-f) și forța lirei (lb-f).

Indice articol

• 1 Cum se calculează? 
• 2 exerciții rezolvate
  • 2.1 - Exercițiul 1
  • 2.2 Exercițiul 2
• 3 Referințe

Cum se calculează? 

Pentru a calcula valoarea sarcinii radiale pe elementele unei structuri, trebuie urmați următorii pași:

- Realizați diagrama forțelor pe fiecare element.

- Aplicați ecuațiile care garantează echilibrul translațional; adică suma tuturor forțelor este zero.

- Luați în considerare ecuația cuplurilor sau momentelor, astfel încât echilibrul de rotație să fie satisfăcut. În acest caz, suma tuturor cuplurilor trebuie să fie zero.

- Calculați forțele pentru a putea identifica sarcinile radiale care acționează asupra fiecărui element.

Exerciții rezolvate

-Exercitiul 1

Următoarea figură arată o scripete prin care trece o scripete tensionată cu tensiunea T. Scripeta este montată pe un arbore susținut de doi rulmenți. Centrul unuia dintre ele se află la o distanță L₁ din centrul fuliei. La celălalt capăt se află celălalt rulment, la distanța L_Două.

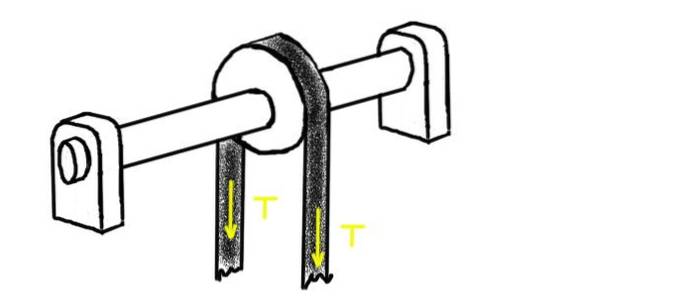
Determinați sarcina radială pe fiecare dintre rulmenți, presupunând că greutatea arborelui și a fuliei sunt semnificativ mai mici decât solicitarea aplicată.

Luați ca valoare pentru tensiunea centurii 100 kg-f și pentru distanțele L₁= 1 m și L_Două= 2 m.

Soluţie

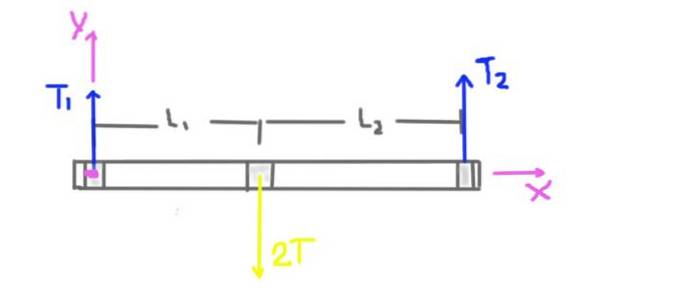
În primul rând, se face o diagramă a forțelor care acționează pe axă.

Tensiunea fuliei este T, dar sarcina radială pe arbore în poziția fuliei este de 2T. Greutatea arborelui și a fuliei nu este luată în considerare deoarece afirmația problemei ne spune că este considerabil mai mică decât tensiunea aplicată centurii.

Reacția radială a suporturilor de pe arbore este cauzată de forțele radiale sau sarcinile T1 și T2. Distanțele L1 și L2 de la suporturi până la centrul fuliei sunt, de asemenea, indicate în diagramă..

De asemenea, este afișat sistemul de coordonate. Cuplul sau momentul total pe axă vor fi calculate luând ca centru originea sistemului de coordonate și vor fi pozitive în direcția Z.

Condiții de echilibru

Acum sunt stabilite condițiile de echilibru: suma forțelor egale cu zero și suma cuplurilor egală cu zero.

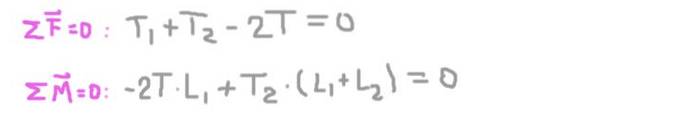
Din a doua ecuație obținem reacția radială pe axă în suportul 2 (T_Două), substituind în prima și rezolvând reacția radială pe axa de la suportul 1 (T₁).

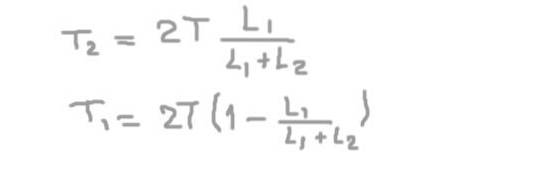
T₁= (2/3) T = 66,6 kg-f

Și sarcina radială pe arbore în poziția suportului 2 este:

T_Două= (4/3) T = 133,3 kg-f.

Exercițiul 2

Următoarea figură prezintă un sistem format din trei scripete A, B, C toate cu aceeași rază R. Scripetele sunt conectate printr-o curea care are o tensiune T.

Arborii A, B, C trec prin lagăre lubrifiate. Separarea dintre centrele axelor A și B este de 4 ori mai mare decât raza R. În mod similar, separarea dintre axele B și C este de asemenea 4R.

Determinați sarcina radială pe axele fuliilor A și B, presupunând că tensiunea curelei este de 600N.

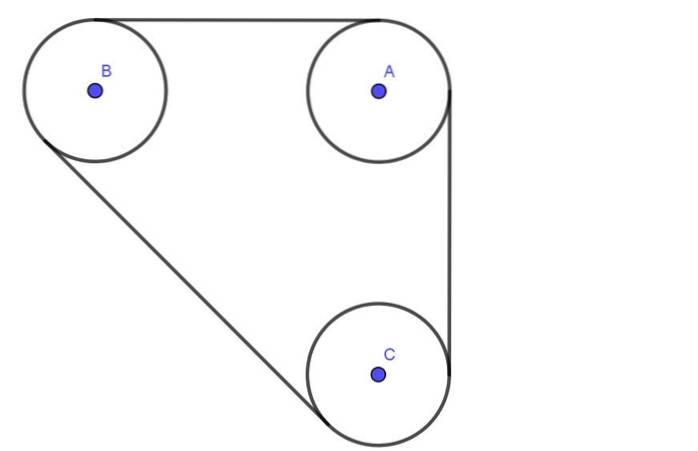
Soluţie

Începem prin a desena o diagramă a forțelor care acționează pe scripetele A și B. Pe prima avem cele două tensiuni T₁ Si t_Două, precum și forța F_LA că rulmentul se exercită pe axa A a scripetei.

În mod similar, pe scripetele B avem tensiunile T₃ , T₄ iar forța F_B că rulmentul se exercită pe axa aceluiași. Sarcina radială pe axa fuliei A este forța F_LA iar sarcina radială pe B este forța F_B.

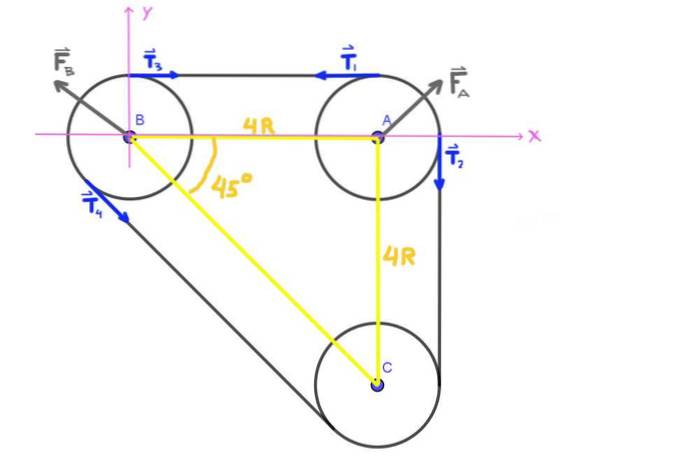
Deoarece axele A, B, C formează un triunghi izorectangular, unghiul ABC este de 45 °.

Toate tensiunile T₁ , T_Două , T₃ , T₄ prezentate în figură au același modul T, care este tensiunea centurii.

Starea echilibrului pentru scripete A

Acum scriem condiția de echilibru pentru scripete A care nu este altceva decât suma tuturor forțelor care acționează asupra scripetei A trebuie să fie zero.

Se separă componentele X și Y ale forțelor și se adaugă (vectorial) următoarea pereche de ecuații scalare:

F_LAX - T = 0; F_LADa - T = 0

Aceste ecuații duc la următoarea egalitate: F_TOPOR = F_OH = T.

Prin urmare, sarcina radială are magnitudinea dată de:

F_LA = (T² + T²)^1/2 = 2^1/2∙ T = 1,41 ∙ T = 848,5 N. cu direcția de 45 °. 

Starea echilibrului pentru scripete B

În mod similar, scriem condiția de echilibru pentru scripetele B. Pentru componenta X avem: F_BX + T + T ∙ Cos45 ° = 0

Y pentru componenta Y: F_BDa + T ∙ Sen45 ° = 0

Prin urmare:

F_BX = - T (1 + 2^-1/2) și F_DE = -T ∙ 2^-1/2

Adică, mărimea sarcinii radiale pe scripetele B este:

F_B = ((1 + 2^-1/2) ² + 2^-1)^1/2∙ T = 1,85 ∙ T = 1108,66 N și direcția sa este de 135 °.

Referințe

1. Beer F, Johnston E, DeWolf J, Mazurek, D. Mecanica materialelor. A cincea ediție. 2010. Mc Graw Hill. 1-130.
2. Gere J, Goodno, B. Mecanica materialelor. A opta ediție. Cengage Learning. 4-220.
3. Giancoli, D. 2006. Fizică: principii cu aplicații. 6^{al treilea} Ed. Prentice Hall. 238-242.
4. Hibbeler R. Mecanica materialelor. A opta ediție. Prentice Hall. 2011. 3-60.
5. Valera Negrete, J. 2005. Note despre fizica generală. UNAM. 87-98.