
Distribuția Chi-pătrat (²), modul de calcul, exemple
Dovada Chi pătrat sau chi-pătrat (χDouă, unde χ este litera greacă numită „chi”) este utilizată pentru a determina comportamentul unei anumite variabile și, de asemenea, atunci când doriți să știți dacă două sau mai multe variabile sunt statistic independente.
Pentru a verifica comportamentul unei variabile, se apelează testul care trebuie efectuat chi pătrat test de potrivire. Pentru a afla dacă două sau mai multe variabile sunt statistic independente, se apelează testul chi pătrat al independenței, numit si contingență.
Aceste teste fac parte din teoria deciziilor statistice, în care se studiază o populație și se iau decizii cu privire la aceasta, analizând unul sau mai multe eșantioane prelevate din aceasta. Pentru aceasta este necesar să se facă anumite ipoteze despre variabile, numite ipoteză, ceea ce poate fi sau nu adevărat.
Există câteva teste pentru a contrasta aceste presupuneri și a determina care sunt valabile, într-o anumită marjă de încredere, inclusiv testul chi-pătrat, care poate fi aplicat pentru a compara două și mai multe populații..
După cum vom vedea, de obicei sunt ridicate două tipuri de ipoteze despre un anumit parametru de populație în două eșantioane: ipoteza nulă, numită Hsau (probele sunt independente), iar ipoteza alternativă, notată ca H1, (probele sunt corelate) ceea ce este opusul.
Indice articol
- 1 Când se folosește testul chi-pătrat?
- 1.1 Condiții pentru aplicarea acestuia
- Distribuția 2 pătrat Chi
- 2.1 Gradele de libertate
- 2.2 Formularea ipotezelor
- 3 Cum se calculează statistica chi-pătrat?
- 3.1 Criterii de acceptare pentru Ho
- 4 Exemplu de calcul
- 5 Referințe
Când se folosește testul chi-pătrat?
Testul chi pătrat se aplică variabilelor care descriu calități, cum ar fi sexul, starea civilă, grupa sanguină, culoarea ochilor și preferințele de diferite tipuri.
Testul este destinat atunci când doriți:
-Verificarea dacă o distribuție este adecvată pentru a descrie o variabilă, care se numește bunătatea potrivirii. Folosind testul chi-pătrat, este posibil să știm dacă există diferențe semnificative între distribuția teoretică selectată și distribuția de frecvență observată..
-Aflați dacă două variabile X și Y sunt independente din punct de vedere statistic. Acest lucru este cunoscut sub numele de test de independență.
Deoarece este aplicat variabilelor calitative sau categorice, testul chi-pătrat este utilizat pe scară largă în științe sociale, management și medicină..
Condiții pentru aplicarea acestuia
Există două cerințe importante pentru ao aplica corect:
-Datele trebuie grupate în frecvențe.
-Eșantionul trebuie să fie suficient de mare pentru ca distribuția chi-pătrat să fie valabilă, altfel valoarea sa este supraestimată și duce la respingerea ipotezei nule atunci când nu ar trebui să fie cazul..
Regula generală este că, dacă o frecvență cu o valoare mai mică de 5 apare în datele grupate, aceasta nu este utilizată. Dacă există mai multe frecvențe mai mici de 5, atunci acestea trebuie combinate într-o singură pentru a obține o frecvență cu o valoare numerică mai mare de 5.
Distribuție Chi pătrat
χDouă este o distribuție continuă a probabilităților. De fapt, există diferite curbe, în funcție de un parametru k numit grade de libertate a variabilei aleatorii.
Proprietățile sale sunt:
-Aria de sub curbă este egală cu 1.
-Valorile lui χDouă sunt pozitivi.
-Distribuția este asimetrică, adică are o părtinire.
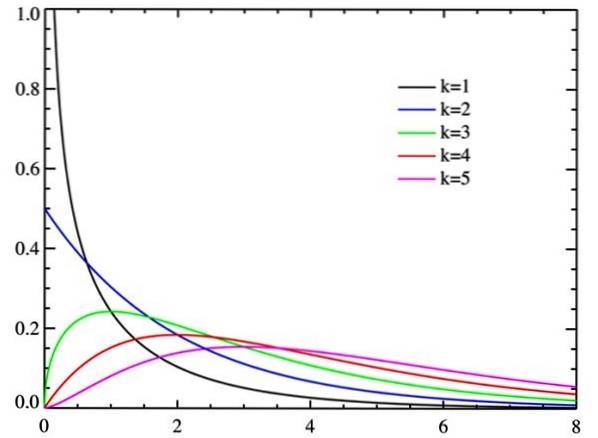
Grade de libertate
Pe măsură ce cresc gradele de libertate, distribuția chi-pătrat tinde spre normalitate, după cum se poate vedea din figură.
Pentru o distribuție dată, gradele de libertate sunt determinate prin tabelul de contingență, care este tabelul unde sunt înregistrate frecvențele observate ale variabilelor.
Dacă o masă are F rânduri și c coloane, valoarea k este:
k = (f - 1) ⋅ (c - 1)
Formularea ipotezelor
Când testul chi-pătrat este potrivit, se formulează următoarele ipoteze:
-Hsau: variabila X are o distribuție de probabilitate f (x) cu parametrii specifici y1, DaDouă…, Yp
-H1: X are o altă distribuție de probabilitate.
Distribuția de probabilitate asumată în ipoteza nulă poate fi, de exemplu, distribuția normală cunoscută, iar parametrii ar fi media μ și abaterea standard σ.
În plus, ipoteza nulă este evaluată cu un anumit nivel de semnificație, adică o măsură a erorii care ar fi comisă atunci când respingerea este adevărată.
De obicei, acest nivel este setat la 1%, 5% sau 10% și cu cât este mai mic, cu atât rezultatul testului este mai fiabil..
Și dacă se folosește testul chi-pătrat al contingenței, care, așa cum am spus, servește pentru a verifica independența dintre două variabile X și Y, ipotezele sunt:
-Hsau: variabilele X și Y sunt independente.
-H1: X și Y sunt dependente.
Din nou, este necesar să se specifice un nivel de semnificație pentru a cunoaște măsura erorii la luarea deciziei..
Cum se calculează statistica chi-pătrat?
Statistica chi pătrat este calculată după cum urmează:

Suma se efectuează de la prima clasă i = 1 până la ultima, care este i = k.
Ce este mai mult:
-Fsau este o frecvență observată (provine din datele obținute).
-Fși este frecvența așteptată sau teoretică (trebuie calculată din date).
Pentru a accepta sau respinge ipoteza nulă, calculăm χDouă pentru datele observate și comparate cu o valoare numită chi pătrat critic, care depinde de gradele de libertate k și nivelul de semnificație α:
χDouăcritic = χDouăk, α
Dacă, de exemplu, dorim să efectuăm testul cu un nivel de semnificație de 1%, atunci α = 0,01, dacă va fi cu 5%, atunci α = 0,05 și așa mai departe. Definim p, parametrul distribuției, ca:
p = 1 - α
Aceste valori critice chi pătrat sunt determinate de tabele care conțin valoarea cumulativă a ariei. De exemplu, pentru k = 1, care reprezintă 1 grad de libertate și α = 0,05, care este egal cu p = 1- 0,05 = 0,95, valoarea lui χDouă este de 3.841.

H criterii de acceptaresau
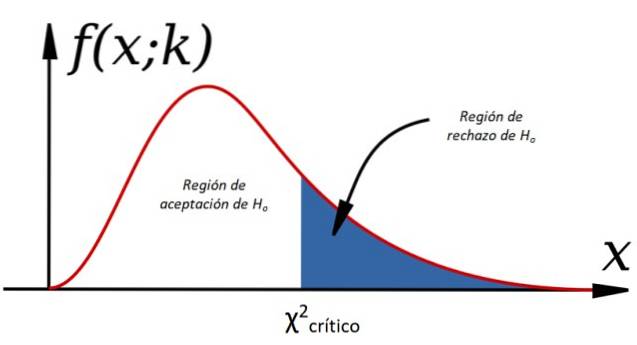
Criteriul de acceptare a lui Hsau este:
-Da χDouă < χDouăcritic H este acceptatsau, altfel este respins (vezi figura 1).
Exemplu de calcul
În următoarea aplicație, testul chi pătrat va fi folosit ca test de independență.
Să presupunem că cercetătorii doresc să știe dacă preferința pentru cafeaua neagră este legată de sexul persoanei și specifică răspunsul cu un nivel de semnificație α = 0,05.
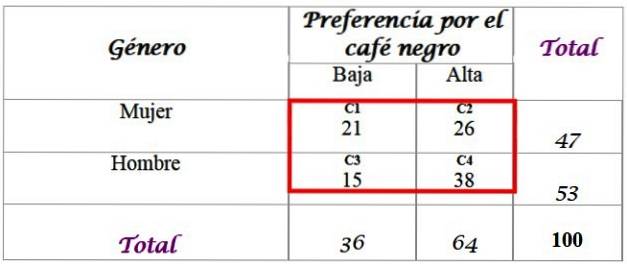
Pentru aceasta, un eșantion de 100 de persoane intervievate și răspunsurile lor sunt disponibile:
Pasul 1
Stabiliți ipotezele:
-Hsau: sexul și preferința pentru cafeaua neagră sunt independente.
-H1: gustul pentru cafeaua neagră este legat de genul persoanei.
Pasul 2
Calculați frecvențele așteptate pentru distribuție, pentru care sunt necesare totalurile adăugate în ultimul rând și în coloana din dreapta a tabelului. Fiecare celulă din caseta roșie are o valoare așteptată Fși, care se calculează înmulțind totalul rândului dvs. F cu totalul coloanei dvs. C, împărțit la totalul eșantionului N:
Fși = (F x C) / N
Rezultatele sunt următoarele pentru fiecare celulă:
-C1: (36 x 47) / 100 = 16,92
-C2: (64 x 47) / 100 = 30,08
-C3: (36 x 53) / 100 = 19,08
-C4: (64 x 53) / 100 = 33,92
Pasul 3
Apoi, statistica chi-pătrat trebuie calculată pentru această distribuție, conform formulei date:

Pasul 4
Determinați χDouăcritic, știind că datele înregistrate sunt în f = 2 rânduri și c = 2 coloane, prin urmare, numărul de grade de libertate este:
k = (2-1) ⋅ (2-1) = 1.
Ceea ce înseamnă că trebuie să căutăm în tabelul de mai sus valoarea χDouăk, α = χDouă1; 0,05 , care este:
χDouăcritic = 3.841
Pasul 5
Comparați valorile și decideți:
χDouă = 2,9005
χDouăcritic = 3.841
Din moment ce χDouă < χDouăcritic se acceptă ipoteza nulă și se concluzionează că preferința pentru cafeaua neagră nu este legată de sexul persoanei, cu un nivel de semnificație de 5%.
Referințe
- Testul Chi Square pentru independență. Recuperat de la: saylordotorg.github.io.
- Med Wave. Statistici aplicate științelor sănătății: testul chi-pătrat. Recuperat de pe: medwave.cl.
- Probabilități și statistici. Test de bunătate de potrivire Chi-pătrat. Recuperat de pe: probayestadistica.com.
- Triola, M. 2012. Statistici elementare. 11. Ediție. Addison Wesley.
- UNAM. Testul pătratului Chi. Recuperat de la: asesorias.cuautitlan2.unam.mx.



Nimeni nu a comentat acest articol încă.