Ciclul Brayton este un ciclu termodinamic care constă din patru procese și se aplică unui fluid termodinamic comprimabil, cum ar fi un gaz. Prima sa mențiune datează de la sfârșitul secolului al XVIII-lea, deși a trecut ceva timp până când a fost ridicată pentru prima dată de James Joule. Acesta este motivul pentru care este cunoscut și sub numele de ciclul Joule..
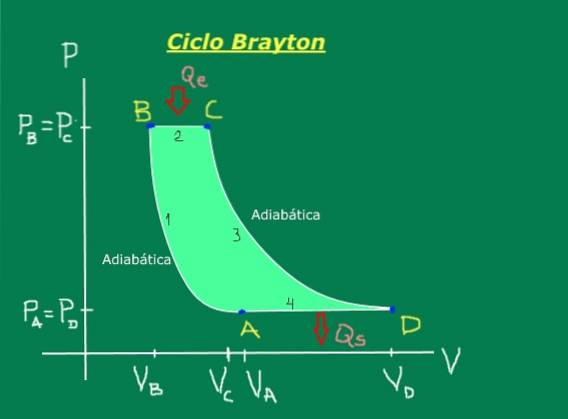
Se compune din următoarele etape, care sunt ilustrate în mod convenabil în diagrama presiune-volum din figura 1: compresie adiabatică (nu se schimbă căldură), expansiune izobarică (are loc la presiune constantă), expansiune adiabatică (nu se schimbă căldură) și compresie izobarică (apare la presiune constantă).
Indice articol
Ciclul Brayton este ciclul termodinamic ideal care se aplică cel mai bine pentru a explica funcționarea termodinamică a turbinelor cu gaz și a amestecului aer-combustibil, utilizate pentru generarea de energie electrică și în motoarele aeronavelor..
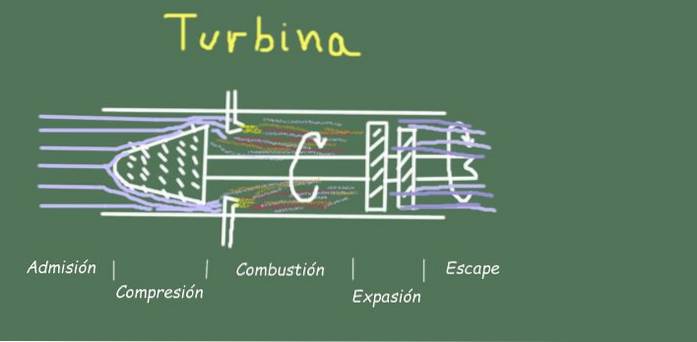
De exemplu, în funcționarea unei turbine există mai multe etape în fluxul de gaz de funcționare, pe care le vom vedea mai jos.
Se compune din intrarea aerului la temperatura ambiantă și presiune prin deschiderea de admisie a turbinei.
Aerul este comprimat prin rotirea lamelor împotriva lamelor fixe din secțiunea compresorului turbinei. Această compresie este atât de rapidă încât practic nu există schimb de căldură, deci este modelată de procesul adiabatic AB al ciclului Brayton. Aerul la ieșirea compresorului și-a crescut presiunea și temperatura.
Aerul este amestecat cu gaz propan sau combustibil pulverizat care este introdus prin injectoarele camerei de ardere. Amestecul produce o reacție chimică de ardere.
Această reacție este cea care asigură căldura care crește temperatura și energia cinetică a particulelor de gaz care se extind în camera de ardere la presiune constantă. În ciclul Brayton acest pas este modelat cu procesul BC care are loc la presiune constantă.
În secțiunea turbinei în sine, aerul continuă să se extindă împotriva paletelor turbinei, provocând rotirea acesteia și producând lucrări mecanice. În acest pas, aerul își scade temperatura, dar fără a schimba practic căldura cu mediul înconjurător..
În ciclul Brayton acest pas este simulat ca un proces de expansiune adiabatică a CD-ului. O parte din activitatea turbinei este transferată la compresor, iar cealaltă este utilizată pentru a acționa un generator sau o elice.
Aerul de ieșire se află la o presiune constantă egală cu presiunea ambiantă și transferă căldura către masa enormă de aer extern, deci într-un timp scurt preia aceeași temperatură ca și aerul de intrare. În ciclul Brayton acest pas este simulat cu procesul DA de presiune constantă, închizând ciclul termodinamic.
Propunem să calculăm eficiența ciclului Brayton, pentru care pornim de la definirea acestuia.
Într-un motor termic, eficiența este definită ca munca netă realizată de mașină împărțită la energia termică furnizată.
Primul principiu al termodinamicii afirmă că căldura netă contribuită la un gaz într-un proces termodinamic este egală cu modificarea energiei interne a gazului plus munca depusă de acesta..
Dar într-un ciclu complet, variația energiei interne este zero, deci căldura netă contribuită în ciclu este egală cu munca netă realizată..
Expresia anterioară ne permite să scriem eficiența în funcție de căldura absorbită sau de intrare Qe (pozitivă) și de căldura transferată sau de ieșire Qs (negativă).
În ciclul Brayton, căldura intră în procesul izobaric BC și iese în procesul isobaric DA.
Presupunând că n moli de gaz la presiune constantă sunt alimentate cu căldură sensibilă Qe în procesul BC, atunci temperatura sa crește de la Tb la Tc în conformitate cu următoarea relație:
Căldură ieșită Întrebări poate fi calculat în mod similar prin următoarea relație care se aplică procesului de presiune constantă DA:
Înlocuind aceste expresii în expresia care ne dă eficiența în funcție de căldura de intrare și de căldură, făcând simplificările pertinente, se obține următoarea relație pentru eficiență:
Este posibil să simplificăm rezultatul anterior dacă luăm în considerare acest lucru Pa = Pd Și ce dacă Pb = Pc deoarece procesele AD și BC sunt izobarice, adică la aceeași presiune.
Mai mult, deoarece procesele AB și CD sunt adiabatice, raportul Poisson este îndeplinit pentru ambele procese:
Unde gamma reprezintă coeficientul adiabatic, adică coeficientul dintre capacitatea de căldură la presiune constantă și capacitatea de căldură la volum constant.
Folosind aceste relații și relația din ecuația de stare a gazului ideal putem obține o expresie alternativă pentru raportul lui Poisson:
De unde știm asta Pa = Pd Și ce dacă Pb = Pc substituind și împărțind elementul cu elementul se obține următoarea relație între temperaturi:
Dacă fiecare membru al ecuației anterioare este scăzut de unitate, diferența este rezolvată și termenii sunt aranjați, se poate arăta că:
Expresia obținută pentru eficiența ciclului Brayton în funcție de temperaturi poate fi rescrisă pentru a fi formulată în funcție de coeficientul presiunii la ieșirea și intrarea compresorului.
Acest lucru se realizează dacă raportul Poisson dintre punctele A și B este cunoscut ca o funcție de presiune și temperatură, obținându-se astfel că eficiența ciclului este exprimată după cum urmează:
Un raport tipic de presiune este 8. În acest caz, ciclul Brayton are un randament teoretic de 45%..
Ciclul Brayton ca model se aplică turbinelor cu gaz care sunt utilizate în centralele termoelectrice pentru a deplasa generatoarele care produc electricitate.
Este, de asemenea, un model teoretic care se potrivește foarte bine funcționării motoarelor cu turbopropulsor utilizate în aeronave, dar nu este deloc aplicabil în turboreactoare..
Când doriți să maximizați munca produsă de turbină pentru a muta generatoarele sau elicele unui avion, atunci se aplică ciclul Brayton..
Pe de altă parte, la turboreactoarele de avion, nu este interesant să se convertească energia cinetică a gazelor de ardere pentru a produce muncă, ceea ce ar fi suficient pentru a reîncărca turbocompresorul..
Dimpotrivă, este important să se obțină cea mai mare energie cinetică posibilă a gazului expulzat, astfel încât, conform principiului de acțiune și reacție, să se obțină impulsul aeronavei..
O turbină cu gaz utilizată în centralele termoelectrice are o presiune la ieșirea compresorului de 800 kPa. Temperatura gazului de intrare este ambiantă și este de 25 Celsius, iar presiunea este de 100 kPa.
În camera de ardere temperatura crește până la 1027 Celsius pentru a intra în turbină.
Determinați eficiența ciclului, temperatura gazului la ieșirea compresorului și temperatura gazului la ieșirea turbinei.
Deoarece avem presiunea gazului la ieșirea compresorului și știm că presiunea de intrare este presiunea atmosferică, atunci este posibil să se obțină raportul de presiune:
r = Pb / Pa = 800 kPa / 100 KPa = 8
Deoarece gazul cu care operează turbina este un amestec de aer și gaz propan, coeficientul adiabatic este apoi aplicat pentru un gaz ideal diatomic, adică o gamă de 1,4.
Eficiența ar fi apoi calculată astfel:
În cazul în care am aplicat relația care dă eficiența ciclului Brayton în funcție de raportul de presiune din compresor.
Pentru a determina temperatura la ieșirea compresorului sau care este aceeași cu temperatura cu care gazul intră în camera de ardere, aplicăm relația eficienței cu temperaturile de intrare și ieșire ale compresorului.
Dacă rezolvăm temperatura Tb din acea expresie, obținem:
Ca date pentru exercițiu avem că după ardere temperatura crește la 1027 Celsius, pentru a intra în turbină. O parte din energia termică a gazului este utilizată pentru a mișca turbina, astfel încât temperatura la ieșirea sa trebuie să fie mai mică.
Pentru a calcula temperatura la ieșirea turbinei vom folosi o relație între temperatura obținută anterior:
De acolo rezolvăm ca Td să obțină temperatura la ieșirea turbinei. După efectuarea calculelor, temperatura obținută este:
Td = 143,05 Celsius.
O turbină cu gaz urmează ciclul Brayton. Raportul de presiune între intrarea și ieșirea compresorului este de 12.
Să presupunem că temperatura ambiantă este de 300 K. Ca date suplimentare, se știe că temperatura gazului după ardere (înainte de intrarea în turbină) este de 1000 K.
Determinați temperatura la ieșirea compresorului și temperatura la ieșirea turbinei. De asemenea, determinați câte kilograme de gaz circulă prin turbină în fiecare secundă, știind că puterea sa este de 30 KW.
Să presupunem căldura specifică a gazului ca fiind constantă și să luăm valoarea sa la temperatura camerei: Cp = 1,0035 J / (kg K).
Să presupunem, de asemenea, că eficiența compresiei în compresor și eficiența decompresiei în turbină este de 100%, ceea ce este o idealizare, deoarece în practică apar întotdeauna pierderi..
Pentru a determina temperatura la ieșirea compresorului, cunoscând temperatura de intrare, trebuie să ne amintim că este o compresie adiabatică, astfel încât raportul Poisson poate fi aplicat pentru procesul AB.
Pentru orice ciclu termodinamic, lucrul net va fi întotdeauna egal cu căldura netă schimbată în ciclu..
Lucrul net pe ciclu de funcționare poate fi apoi exprimat ca o funcție a masei de gaz care a circulat în acel ciclu și a temperaturilor.
În această expresie m este masa de gaz care a circulat prin turbină într-un singur ciclu de funcționare și Cp căldura specifică.
Dacă luăm derivata în raport cu timpul expresiei anterioare, obținem puterea medie netă în funcție de fluxul de masă.
Clearing out m punct, și înlocuind temperaturile, puterea și capacitatea termică a gazului, obținem un flux de masă de 1578,4 kg / s.
Nimeni nu a comentat acest articol încă.