Formule ale coeficientului de corelație, calcul, interpretare, exemplu

coeficient de corelație în statistici este un indicator care măsoară tendința a două variabile cantitative X și Y de a avea o relație liniară sau proporțională între ele.

În general, perechile de variabile X și Y sunt două caracteristici ale aceleiași populații. De exemplu, X poate fi înălțimea unei persoane și Y greutatea sa..

În acest caz, coeficientul de corelație ar indica dacă există sau nu o tendință către o relație proporțională între înălțime și greutate într-o populație dată..

Coeficientul de corelație liniară al lui Pearson este notat cu litera r litere mici și valorile sale minime și maxime sunt -1 și respectiv +1. 

O valoare r = +1 ar indica faptul că setul de perechi (X, Y) sunt perfect aliniate și că atunci când X crește, Y va crește în aceeași proporție. Pe de altă parte, dacă s-ar întâmpla ca r = -1, și setul de perechi ar fi perfect aliniat, dar în acest caz când X crește, Y scade în aceeași proporție.

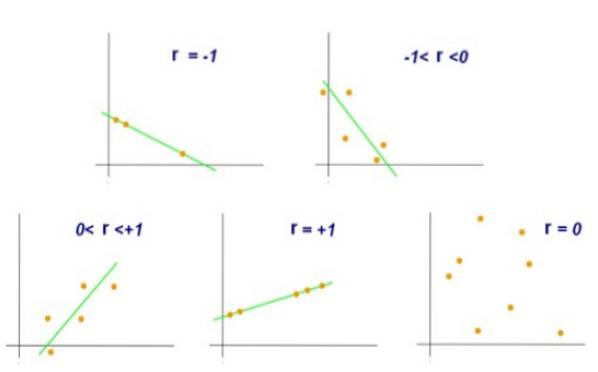
Pe de altă parte, o valoare r = 0 ar indica faptul că nu există o corelație liniară între variabilele X și Y. În timp ce o valoare r = +0,8 ar indica faptul că perechile (X, Y) tind să se grupeze pe o parte și altul dintr-o anumită dreaptă.

Formula pentru calcularea coeficientului de corelație r este următoarea:

Cum se calculează coeficientul de corelație?

Coeficientul de corelație liniară este o cantitate statistică găsită în calculatoarele științifice, în majoritatea foilor de calcul și în programele statistice..

Cu toate acestea, este convenabil să știți cum se aplică formula care o definește, iar pentru aceasta se va afișa un calcul detaliat, efectuat pe un set de date mic..

Și așa cum s-a spus în secțiunea anterioară, coeficientul de corelație este covarianța Sxy împărțită la produsul deviației standard Sx pentru variabilele X și Sy pentru variabila Y.

Covarianță și varianță

Covarianța Sxy este:

Sxy = [Σ (Xi - ) (Yi - )] / (N-1)

Unde suma merge de la 1 la N perechi de date (Xi, Yi). și sunt mijloacele aritmetice ale datelor Xi și respectiv Yi.

La rândul său, abaterea standard pentru variabila X este rădăcina pătrată a varianței setului de date Xi, cu i de la 1 la N:

Sx = √ [Σ (Xi - ) ^ 2) / (N-1)]

În mod similar, abaterea standard pentru variabila Y este rădăcina pătrată a varianței setului de date Yi, cu i de la 1 la N:

Sy = √ [Σ (Yi - )^Două ) / (N-1)]

Caz ilustrativ

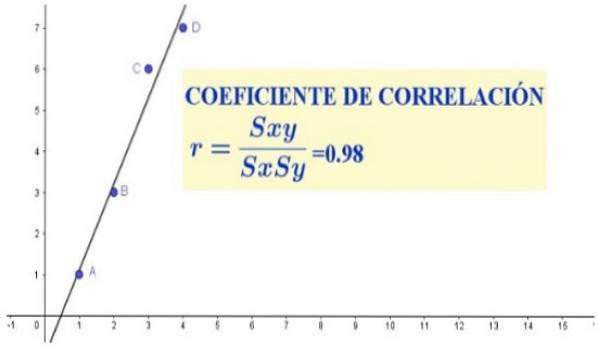
Pentru a arăta în detaliu cum se calculează coeficientul de corelație, vom lua următorul set de patru perechi de date 

(X, Y): (1, 1); (2. 3); (3, 6) și (4, 7).

Mai întâi calculăm media aritmetică pentru X și Y, după cum urmează:

= (1 + 2 + 3 + 4) / 4 = 2,5

= (1 + 3 + 6 + 7) / 4 = 4,25

Apoi se calculează parametrii rămași:

Covarianță Sxy

Sxy = [(1 - 2,5) (1 - 4,25) + (2 - 2,5) (3 - 4,25) + (3 - 2,5) (6 - 4,25) + .... (4 - 2,5) (7 - 4,25) ] / (4-1)

Sxy = [(-1,5) (- 3,25) + (-0,5) (- 1,25) + (0,5) (1,75) + ... . 

.... (1,5) (2,75)] / (3) = 10,5 / 3 = 3.5

Abaterea standard Sx

Sx = √ [(-1,5)^Două + (-0,5)^Două + (0,5)^Două + (1,5)^Două) / (4-1)] = √ [5/3] = 1.29

Deviația standard Sy

Sx = √ [(-3.25)^Două + (-1,25)^Două + (1,75)^Două + (2,75)^Două) / (4-1)] = 

√ [22.75 / 3] = 2,75

Coeficientul de corelație r

r = 3,5 / (1,29 * 2,75) = 0,98

Interpretare

În setul de date din cazul precedent, se observă o corelație liniară puternică între variabilele X și Y, care se manifestă atât în ​​graficul de dispersie (prezentat în Figura 1), cât și în coeficientul de corelație, care a dat o valoare destul de apropiată de unitate.

În măsura în care coeficientul de corelație este mai apropiat de 1 sau -1, cu atât are mai mult sens să se potrivească datele la o linie, rezultatul regresiei liniare..

Regresie liniara

Linia de regresie liniară se obține din Metoda celor mai mici pătrate. în care parametrii liniei de regresie sunt obținuți din minimizarea sumei pătratului diferenței dintre valoarea Y estimată și Yi a datelor N.

Pe de altă parte, parametrii a și b ai liniei de regresie y = a + bx, obținuți prin metoda celor mai mici pătrate, sunt:

* b = Sxy / (Sx^Două) Pentru panta

* a = - b pentru intersecția liniei de regresie cu axa Y..

Reamintim că Sxy este covarianța definită mai sus și Sx^Două este varianța sau pătratul abaterii standard definite mai sus. și sunt mijloacele aritmetice ale datelor X și respectiv Y.

Exemplu

Coeficientul de corelație este utilizat pentru a determina dacă există o corelație liniară între două variabile. Se aplică atunci când variabilele care urmează să fie studiate sunt cantitative și, în plus, se presupune că acestea urmează o distribuție de tip normal..

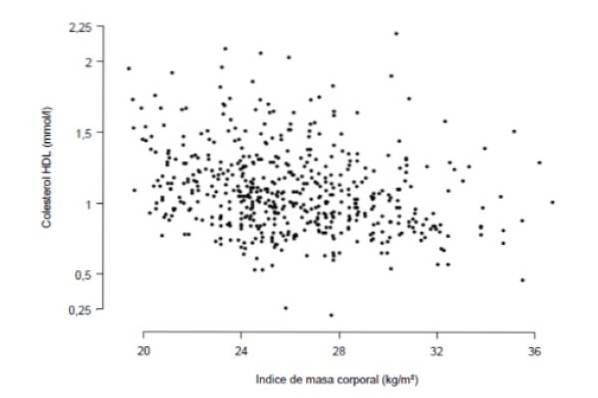
Avem un exemplu ilustrativ mai jos: o măsură a gradului de obezitate este indicele de masă corporală, care se obține prin împărțirea greutății unei persoane în kilograme la înălțimea pătrată a acesteia în unități de metri pătrate.

Vrei să știi dacă există o corelație puternică între indicele de masă corporală și concentrația de colesterol HDL în sânge, măsurată în milimoli pe litru. În acest scop, a fost realizat un studiu cu 533 de persoane, care este rezumat în graficul următor, în care fiecare punct reprezintă datele unei persoane.

Observarea atentă a graficului arată că există o anumită tendință liniară (nu foarte marcată) între concentrația colesterolului HDL și indicele de masă corporală. Măsura cantitativă a acestei tendințe este coeficientul de corelație, care pentru acest caz s-a dovedit a fi r = -0,276.

Referințe

1. González C. Statistici generale. Recuperat de pe: tarwi.lamolina.edu.pe
2. IACS. Institutul Aragonesc de Științe ale Sănătății. Recuperat de pe: ics-aragon.com 
3. Salazar C. și Castillo S. Principiile de bază ale statisticii. (2018). Recuperat de la: dspace.uce.edu.ec
4. Superprof. Coeficient de corelație. Recuperat de pe: superprof.es
5. USAC. Manual de statistici descriptive. (2011). Recuperat de la: statistics.ingenieria.usac.edu.gt
6. Wikipedia. Coeficientul de corelație al lui Pearson. Recuperat de pe: es.wikipedia.com.