conservarea impulsului liniar a unui corp stabilește că produsul masei sale și al vectorului său de viteză este o cantitate constantă, atunci când corpul este liber de interacțiune cu alte corpuri și cu viteza măsurată în raport cu un cadru de referință fix sau neaccelerat.
Când aveți mai multe corpuri care interacționează numai între ele, dar nu cu mediul extern, atunci impuls liniar a setului rămâne, de asemenea, constantă în timp.
Momentul liniar, impulsul sau pur și simplu impuls, se notează cu litera p y este o cantitate vectorială:
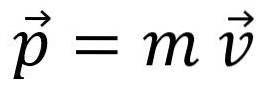
Momentul nu este același cu viteza, deși relația este evidentă: de exemplu, un camion care merge cu 20 km / h are mai mult impuls decât o bicicletă care se mișcă cu aceeași viteză.
Pentru ca impulsul liniar al unui corp să se schimbe, o forță externă netă trebuie să acționeze asupra acestuia, altfel rămâne constantă. De asemenea, momentul liniar P a unui sistem format din n-corpuri este suma vectorială a momentelor individuale:
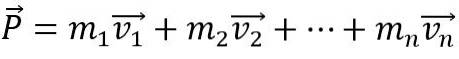
Indice articol
Într-un corp fără forță (sau unul în care toate forțele de pe el se anulează) se întâmplă ca momentul liniar să rămână constant.
Același lucru se întâmplă într-un sistem format din mai multe corpuri care interacționează doar între ele, dar nu și cu mediul extern: impulsul liniar total al sistemului rămâne fix în timpul evoluției mișcării întregului..
Acest principiu de conservare este menționat după cum urmează:
Momentul total al unui set de n-corpuri care interacționează doar între ele, dar nu și cu mediul extern, este o cantitate invariabilă în timp.
Și matematic se exprimă după cum urmează:
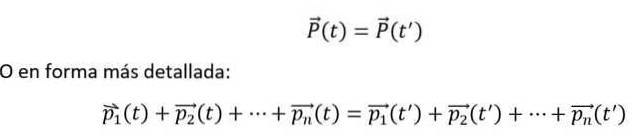
Egalitățile de mai sus sunt îndeplinite, dacă și numai dacă n-corpurile interacționează între ele, dar nu și cu mediul extern. Mai mult, momentele individuale trebuie întotdeauna măsurate în raport cu un cadru de referință inerțial..
Doi astronauți din spațiu se țin de mână și sunt ținuți într-o poziție fixă față de nava spațială. Dar dacă se împing reciproc, încep să se separe în direcții opuse, când sunt văzuți de pe navă..
În acest caz, întrucât interacțiunea dintre astronauți este doar între ei prin forța de contact a mâinilor lor, impulsul total după împingere este încă valoarea inițială cu privire la nava spațială. Adică, impulsul total 0.
Cu toate acestea, impulsul fiecărui astronaut s-a schimbat. Inițial, fiecare avea 0 moment liniar față de navă, dar după ce a fost împins, unul iese într-o direcție și cealaltă în direcția opusă, cu momente liniare diferite de zero cu magnitudine egală și direcții opuse..
Astfel, când momentele individuale sunt adăugate vectorial, impulsul total inițial este obținut ca rezultat, care este zero.
Pe de altă parte, conservarea cantității de impuls indică faptul că astronautul cu cea mai mică masă este cel care se mișcă mai repede față de nava spațială. Dar rezultatul înmulțirii masei sale cu viteza sa este egal cu produsul obținut prin înmulțirea masei celuilalt cu viteza celuilalt.
Un cățeluș se află pe o platformă plutitoare într-un lac calm, iar proprietarul său îl urmărește dintr-un doc. La început, atât platforma, cât și cățelușul sunt odihniți, dar atunci când cățelușul vrea să se apropie de proprietar, platforma se îndepărtează de doc..
Explicația acestei observații se află tocmai în principiul conservării cantității de impuls liniar. Sistemul constă din cățeluș și platformă.
Cățelușul poate merge pe platformă datorită forței de frecare dintre picioare și suprafață, în acest caz forța de frecare este o forță internă de interacțiune între acesta și platformă.
Întregul este un sistem izolat, deoarece platforma se poate deplasa orizontal peste lac, fără nici o rezistență la mișcare. Pe de altă parte, în direcția verticală, toate forțele sunt echilibrate și compensate, iar întregul nu are mișcare în acea direcție..
Prin urmare, în această situație toate ipotezele sunt îndeplinite astfel încât să se aplice principiul conservării impulsului liniar.
Un eschimos este prins în centrul unui lac înghețat, gheața este atât de netedă încât oricât de mult ar încerca, eschimosul alunecă și rămâne întotdeauna în același loc.
Singura modalitate posibilă pentru eschimoși de a ieși din lac este ca el să arunce în direcția opusă la care vrea să mute un obiect greu pe care îl poartă în rucsac (presupunând că poartă unul).
Conservarea impulsului liniar este aplicată pentru a propulsa o rachetă în spațiul cosmic unde nu există forțe externe. În acest caz, impulsul navei este realizat prin expulzarea gazelor la viteză mare, astfel încât racheta să se poată deplasa în direcția opusă la care au fost expulzate..
Dacă inițial nava este în repaus, atunci când arde și expulză combustibil, forța expulzării se produce împotriva navei în sine. Este o forță internă între gaze și navă. Nu există forțe externe și, prin urmare, se aplică conservarea impulsului liniar.
Deoarece impulsul liniar al gazelor este același și opus celui navei, acesta reușește să iasă din odihnă și, continuând să expulzeze gazele, își mărește cantitatea de mișcare și, prin urmare, viteza sa.
Un alt caz de aplicare a conservării impulsului liniar în viața de zi cu zi este de a introduce un cui în lemn, profitând de cantitatea de mișcare sau impulsul ciocanului..
S-ar putea argumenta că, în acest caz, principiul nu se aplică, deoarece există o forță externă: rezistența pe care lemnul o oferă cuiului..
Cu toate acestea, în momentul contactului, forța pe care ciocanul o impune asupra cuiului este o forță internă (între sistemul care este cuiul și ciocanul) mult mai mare decât rezistența pe care o opune lemnul și, prin urmare, aceasta din urmă este neglijabilă..
Tot impulsul ciocanului, care este destul de mare datorită masei și vitezei sale mari, este transferat pe unghie imediat după coliziune. Rețineți că tot timpul, dar nu toată energia cinetică a ciocanului este transferată, întrucât o parte din aceasta este transformată în energie termică în cui și în ciocan, care își cresc temperatura după impact.
Astronauții Andrew și Berenice se află în afara stației spațiale ținându-se de ambele mâini și în repaus față de stație. Acestea sunt propulsate împingând mâinile una împotriva celeilalte și sunt eliberate. Dacă Andrew, 70 kg de masă, se mișcă la 1 m / s față de stație, care este viteza lui Berenice cu 49 kg de masă?
În acest caz, ipotezele conservării impulsului liniar se aplică în mod clar, deoarece nu există forțe externe în spațiul cosmic. Forța cu care ambii astronauți își împing mâinile este o forță internă.
Să presupunem că masa lui Andrew este Mla și cea a lui Berenice Mb. În mod similar, viteza ambelor după impuls este Vla pentru Andrew și Vb pentru Berenice. Apoi, conservarea impulsului liniar se aplică astfel:
Mla∙0 + Mb∙0 = Mla∙Vla+ Mb∙Vb
Rezolvând viteza lui Berenice avem:
Vb = - (Mla / Mb) ∙ Vla
Plasarea valorilor numerice:
Vb = - (70/49) ∙ (1m / s) sau = -1,43m / s sau
Adică, Berenice se mișcă cu o viteză de 1,43 m / s în direcția opusă celei a lui Andrew.
Un cățeluș cu greutatea de 5 kg se află în repaus pe o platformă de 15 kg care plutește, tot în repaus, pe un lac nemișcat. Dacă catelul începe să meargă pe platformă cu o rată de 0,5 m / s în raport cu acesta. Cât de repede vor avea catelul și platforma față de un observator fixat la sol??
Sistemul de referință inerțial va fi luat ca doc în care se află proprietarul cățelușului. Inițial, atât cățelușul, cât și platforma plutitoare sunt în repaus cu privire la doc..
Când cățelușul decide să meargă repede către proprietar v ' față de platformă, atunci platforma se îndepărtează de dig cu viteză +V. Viteza cățelușului față de arc se obține prin suma vectorială a vitezei sale față de platformă plus viteza platformei și o denotăm prin:
v = -v' + V
Deoarece rezistența apei la mișcarea platformei este practic nulă datorită vitezei reduse, atunci se poate afirma că sistemul format din catelul + platforma este un sistem izolat și se aplică principiul conservării impulsului liniar:
0 = m ∙ v + M ∙ V
Amintindu-ne că v = v '+ V avem:
0 = -m ∙ v '+ m ∙ v + M ∙ V
Adică: m ∙ v '= (m + M) ∙ V
Prin urmare V = [m / (m + M)] v 'și v = - (M / m) V = - [M / (m + M)] v'
Înlocuind valorile numerice avem:
V = [5 / (5 +15)] ∙ 0,5m / s = 0,125 m / s
Aceasta este viteza cu care platforma se îndepărtează de doc.
V = - (15/20) ∙ 0,5m / s = -0,375 m / s
Și aceasta este viteza cu care catelul se apropie de doc.
Nimeni nu a comentat acest articol încă.