
Funcții și aplicații trigonometrice ale cercului unitar
cerc de unitate este un cerc de rază egal cu 1, care este de obicei centrat în punctul (0,0) al sistemului de coordonate carteziene X y. Folosit pentru a defini cu ușurință raporturile trigonometrice ale unghiurilor folosind triunghiuri dreptunghiulare.
Ecuația cercului unitar centrat la origine este:
XDouă + DaDouă = 1
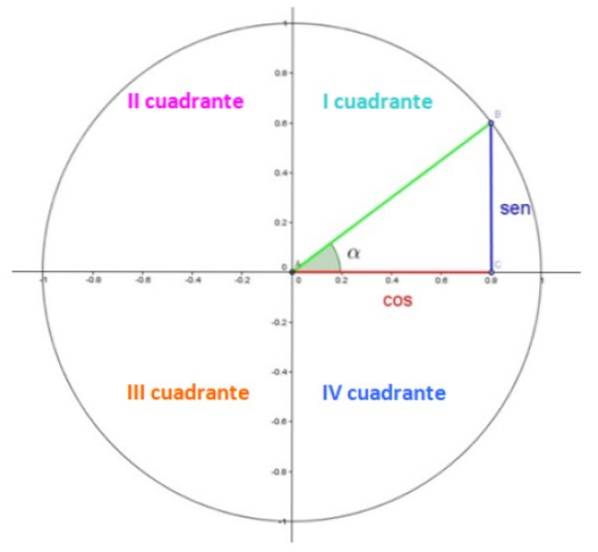
În figura 1 avem cercul unitar, în care fiecare sfert este într-un cadran. Cadrele sunt numerotate cu cifre romane și numărate în sens invers acelor de ceasornic.
În primul cadran există un triunghi. Picioarele, în roșu și albastru, măsoară respectiv 0,8 și 0,6, în timp ce hipotenuza în verde măsoară 1, deoarece este o rază.
Unghiul acut α este un unghi central în poziție standard, ceea ce înseamnă că vârful său coincide cu punctul (0,0) și latura sa inițială cu axa pozitivă x. Unghiul este măsurat în sens invers acelor de ceasornic și i se atribuie un semn pozitiv prin convenție.
Ei bine, în cercul unitar, coordonatele cosinusului și sinusului lui α sunt respectiv coordonatele x și y ale punctului B, care în exemplul prezentat sunt 0,8 și 0,6.
Din aceste două sunt definite:
- tg α = sin α / cos α = 0,6 / 0,8 = 0,75
- sec α = 1 / cos α = 1 / 0,8 = 1,25
- cosec α = 1 / sin α = 1 / 0.6 = 1.66 ...
- ctg α = 1 / tg = 0,8 / 0,6 = 1,33 ...
Indice articol
- 1 Aplicații cerc unitar
- 1.1 Unghiul de referință
- 2 Trasarea graficelor cosinusului și sinusului
- 2.1 Proprietățile funcțiilor sinus și cosinus
- 3 exerciții rezolvate
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 4 Referințe
Aplicații pentru cercuri unitare
Dacă ne limităm la triunghiuri dreptunghiulare, raporturile trigonometrice s-ar aplica numai unghiurilor acute. Cu toate acestea, cu ajutorul cercului unitar, calculul raporturilor trigonometrice este extins la orice unghi α.
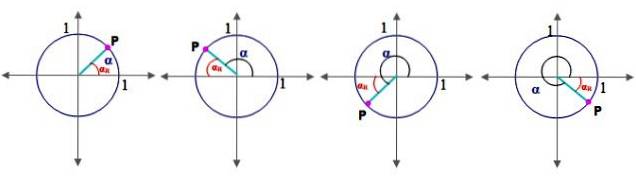
Pentru aceasta, este necesar să se definească mai întâi conceptul de unghi de referință αR:
Unghiul de referință
Fie α un unghi în poziție standard (cel al cărui partea de plecare coincide cu axa x pozitivă), unghiul său de referință αR este între a lui partea terminală și axa x. Figura 2 prezintă unghiul de referință pentru unghiurile din cadranul I, II, III și IV.
Pentru fiecare cadran, unghiul de referință se calculează astfel:
-Primul cadran: αR = α
-Al doilea cadran: αR = 180º - α
-Al treilea cadran: αR = α - 180º
-Al patrulea cadran: αR = 360º - α
Rețineți că primul cadran unghiul α coincide cu unghiul său de referință. Ei bine, raporturile trigonometrice ale unghiului α sunt aceleași cu unghiul lor de referință, cu semnele în conformitate cu cele ale cadranelor în care se încadrează partea terminală a lui α..
Cu alte cuvinte, raportul trigonometric al cosinusului și al sinusurilor unghiului α coincid cu coordonatele punctului P, conform figurii 2.
În figura următoare vedem raporturile trigonometrice ale unor unghiuri notabile, după cum se deduce din cercul unitar.
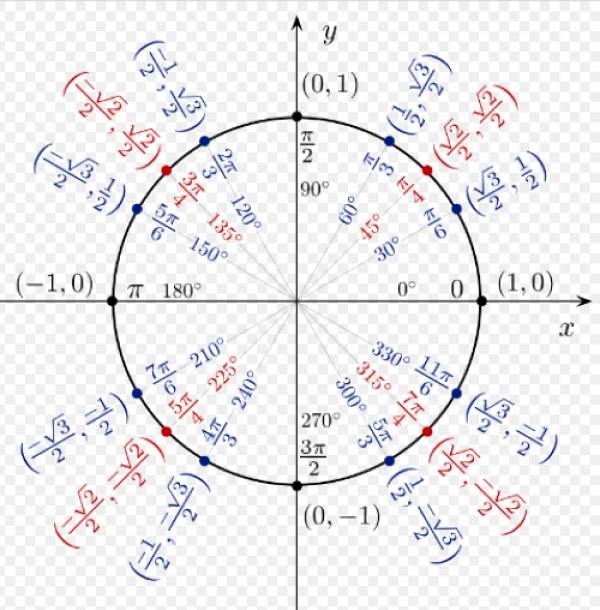
Raporturile cosinusului și sinusului oricărui unghi din cadranul I sunt toate pozitive. Pentru α = 60º avem coordonatele (1/2; √3 / 2), care corespund respectiv cos 60º și sin 60º.
Coordonatele lui α = 120º sunt (-1/2; √3 / 2), deoarece fiind în al doilea cadran, coordonata x este negativă.
Trasarea graficelor cosinusului și sinusului
Cu ajutorul cercului unitar și a coordonatelor punctelor P de pe el, este posibil să trasăm graficele funcțiilor cos t și sin t, așa cum vom vedea mai jos.
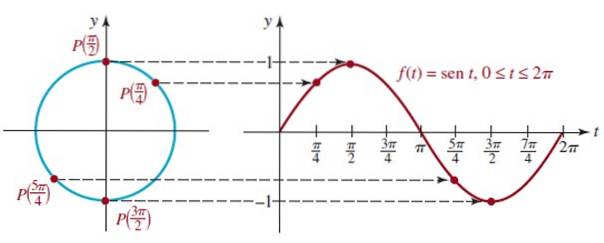
Pentru a face acest lucru, diferite poziții ale punctului P (t) sunt situate pe cercul unității. Vom începe cu graficul funcției f (t) = sin t.
Putem vedea că atunci când trecem de la t = 0 la t = π / 2 (90º) valoarea sin t crește până când ajunge la 1, care este valoarea maximă.
Pe de altă parte, de la t = π / 2 la t = 3π / 2 valoarea sin t scade de la 1, trecând prin 0 la t = π până când atinge minimul -1 la t = 3π / 2.
Figura arată graficul primului ciclu de f (t) = sin t care corespunde primei runde a cercului unitar, această funcție este periodică cu perioada 2π.
Se poate efectua o procedură analogă pentru a obține graficul funcției f (t) = cos t, așa cum se arată în următoarea animație:
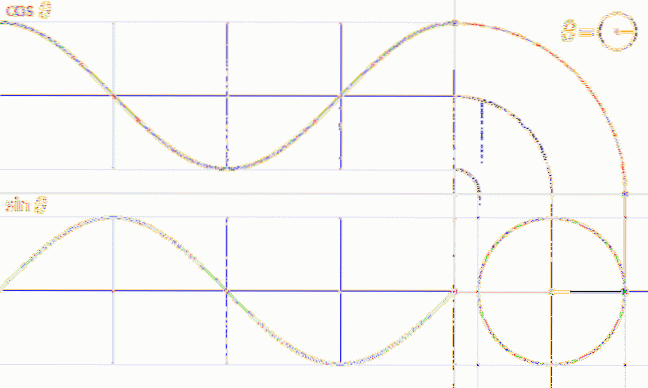
Proprietățile funcțiilor sinus și cosinus
-Ambele funcții sunt continue în setul numerelor reale și, de asemenea, periodice, din perioada 2π.
-Domeniul funcțiilor f (t) = sin t și f (t) = cos t sunt toate numere reale: (-∞, ∞).
-Pentru intervalul sau calea sinusului și cosinusului avem intervalul [-1,1]. Parantezele indică faptul că -1 și 1 sunt incluse.
- Zerourile sin t sunt valorile care corespund cu nπ cu n întreg, în timp ce zerourile cos t sunt [(2n + 1) / 2] cu n și întreg.
-Funcția f (t) = sin t este ciudată, are simetrie în ceea ce privește originea, în timp ce funcția cos t este egală, simetria sa este în jurul axei verticale.
Exerciții rezolvate
- Exercitiul 1
Dat fiind cos t = - 2/5, care este coordonata orizontală a punctului P (t) de pe cercul unității din al doilea cadran, obțineți coordonata verticală corespunzătoare sin t.
Soluţie
Deoarece P (t) aparține cercului unitar, în care este adevărat că:
XDouă + DaDouă = 1
Prin urmare:
y = ± √ 1 - xDouă
Deoarece P (t) se află în al doilea cadran, se va lua valoarea pozitivă. Coordonata verticală a punctului P (t) este y:
y = √ 1 - (-2/5)Două = √0.84
- Exercițiul 2
Un model matematic pentru temperatură T în grade Fahrenheit într-o zi dată, t ore după miezul nopții, este dat de:
T (t) = 50 + 10 sin [(π / 12) × (t - 8)]
Cu t între 0 și 24 de ore. Găsi:
a) Temperatura la 8 dimineața.
b) Ore în care T (t) = 60ºF
c) Temperaturile maxime și minime.
Solutie la
Înlocuim t = 8 în funcția dată:
T (8) = 50 + 10 sin [(π / 12) × (t-8)] = 50 + 10 sin [(π / 12) × (8-8)] =
= 50 + 10 x sin 0 = 50 ºF
Soluția b
50 + 10 sin [(π / 12) × (t-8)] = 60
Este o ecuație trigonometrică și trebuie să rezolvăm necunoscutul „t”:
10 sin [(π / 12) × (t-8)] = 60 - 50 = 10
sin [(π / 12) × (t-8)] = 1
Știm că păcatul π / 2 = 1, prin urmare argumentul sinusului trebuie să fie 1:
(π / 12) × (t-8) = π / 2
t-8 = 6
t = 14 ore
Se concluzionează că la 14 ore după miezul nopții temperatura este de 60 °, adică la 14:00. Nu există alt moment pe tot parcursul zilei (24 de ore) când se întâmplă acest lucru.
Soluția c
Temperatura maximă corespunde valorii la care sin [(π / 12) × (t-8)] = 1 și este 60ºF. Pe de altă parte, minimul apare dacă sin [(π / 12) × (t-8)] = -1 și este 40ºF.
Referințe
- Figuera, J. 1999. Matematică. Primul. Diversificat. Ediții colegiale bolivariene.
- Hoffman, J. Selecția subiectelor de matematică. Volumul 4.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematica este distractivă. Cercul de unitate. Recuperat de la: de: mathsisfun.com.
- Wikipedia. Identități și formule de trigonometrie. Recuperat de pe: es.wikipedia.org.
- Zill, D. 1984. Algebră și trigonometrie. Dealul Mcgraw.



Nimeni nu a comentat acest articol încă.