
Demonstrația inegalității triunghiului, exemple, exerciții rezolvate
Se numeste inegalitatea triunghiului la proprietatea a două numere reale care constau în faptul că valoarea absolută a sumei lor este întotdeauna mai mică sau egală cu suma valorilor lor absolute. Această proprietate este, de asemenea, cunoscută sub numele de inegalitate Minkowski sau inegalitate triunghiulară.
Această proprietate a numerelor se numește inegalitate triunghiulară, deoarece în triunghiuri se întâmplă ca lungimea unei laturi să fie întotdeauna mai mică sau egală cu suma celorlalte două, chiar dacă această inegalitate nu se aplică întotdeauna în aria triunghiurilor..

Există mai multe dovezi ale inegalității triunghiulare în numere reale, dar în acest caz vom alege una pe baza proprietăților valorii absolute și binomului pătrat.
Teorema: Pentru fiecare pereche de numere la Da b referitoare la numerele reale trebuie să:
| a + b | ≤ | la | + | b |
Indice articol
- 1 Demo
- 2 Exemple
- 2.1 Exemplul 1
- 2.2 Exemplul 2
- 2.3 Exemplul 3
- 2.4 Exemplul 4
- 2.5 Exemplul 5
- 2.6 Exemplul 6
- 3 exerciții rezolvate
- 3.1 Exercițiul 1
- 3.2 Exercițiul 2
- 3.3 Exercițiul 3
- 3.4 Exercițiul 4
- 4 Referințe
Demonstrație
Începem prin a lua în considerare primul membru al inegalității, care va fi pătrat:
| a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (ecuația 1)
În pasul anterior, am folosit proprietatea că orice număr pătrat este egal cu valoarea absolută a numărului pătrat, adică: | x | ^ 2 = x ^ 2. S-a folosit și dezvoltarea binomului pătrat.
Toate numărul X este mai mică sau egală cu valoarea sa absolută. Dacă numărul este pozitiv, este egal, dar dacă numărul este negativ, acesta va fi întotdeauna mai mic decât un număr pozitiv. În acest caz, propria sa valoare absolută, adică se poate afirma că x ≤ | x |.
Produsul (a b) este un număr, prin urmare se aplică faptul că (a b) ≤ | a b |. Când această proprietate este aplicată (ecuației 1) avem:
| a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | a b | + b ^ 2 (ecuația 2)
Ținând cont de faptul că | a b | = | a || b | (Ec. 2) poate fi scris după cum urmează:
| a + b | ^ 2 ≤ a ^ 2 + 2 | a || b | + b ^ 2 (ec. 3)
Dar, deoarece am spus anterior că pătratul unui număr este egal cu valoarea absolută a numărului pătrat, atunci ecuația 3 poate fi rescrisă după cum urmează:
| a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | b | + | b | ^ 2 (ec. 4)
În al doilea membru al inegalității, este recunoscut un produs remarcabil, care atunci când este aplicat duce la:
| a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (ecuația 5)
În expresia anterioară, trebuie remarcat faptul că valorile care trebuie pătrate la ambii membri ai inegalității sunt pozitive, prin urmare, trebuie de asemenea satisfăcut că:
| a + b | ≤ (| a | + | b |) (ecuația 6)
Expresia de mai sus este exact ceea ce s-a dorit să demonstreze.
Exemple
În continuare vom verifica inegalitatea triunghiulară cu mai multe exemple.
Exemplul 1
Luăm valoarea a = 2 și valoarea b = 5, adică ambele numere pozitive și verificăm dacă inegalitatea este satisfăcută sau nu.
| 2 + 5 | ≤ | 2 | + | 5 |
| 7 | ≤ | 2 | + | 5 |
7 ≤ 2+ 5
Egalitatea este verificată, prin urmare teorema inegalității triunghiului a fost îndeplinită.
Exemplul 2
Următoarele valori sunt alese a = 2 și b = -5, adică un număr pozitiv și celălalt negativ, verificăm dacă inegalitatea este satisfăcută sau nu.
| 2 - 5 | ≤ | 2 | + | -5 |
| -3 | ≤ | 2 | + | -5 |
3 ≤ 2 + 5
Inegalitatea este satisfăcută, prin urmare a fost verificată teorema inegalității triunghiulare.
Exemplul 3
Luăm valoarea a = -2 și valoarea b = 5, adică un număr negativ și celălalt pozitiv, verificăm dacă inegalitatea este satisfăcută sau nu.
| -2 + 5 | ≤ | -2 | + | 5 |
| 3 | ≤ | -2 | + | 5 |
3 ≤ 2 + 5
Inegalitatea este verificată, prin urmare teorema a fost îndeplinită.
Exemplul 4
Următoarele valori sunt alese a = -2 și b = -5, adică ambele numere negative și verificăm dacă inegalitatea este satisfăcută sau nu.
| -2 - 5 | ≤ | -2 | + | -5 |
| -7 | ≤ | -2 | + | -5 |
7 ≤ 2+ 5
Egalitatea este verificată, prin urmare teorema inegalității lui Minkowski a fost îndeplinită.
Exemplul 5
Luăm valoarea a = 0 și valoarea b = 5, adică un număr zero și celălalt pozitiv, apoi verificăm dacă inegalitatea este satisfăcută sau nu.
| 0 + 5 | ≤ | 0 | + | 5 |
| 5 | ≤ | 0 | + | 5 |
5 ≤ 0+ 5
Egalitatea este îndeplinită, prin urmare teorema inegalității triunghiului a fost verificată.
Exemplul 6
Luăm valoarea a = 0 și valoarea b = -7, adică un număr zero și celălalt pozitiv, apoi verificăm dacă inegalitatea este satisfăcută sau nu.
| 0 - 7 | ≤ | 0 | + | -7 |
| -7 | ≤ | 0 | + | -7 |
7 ≤ 0+ 7
Egalitatea este verificată, prin urmare teorema inegalității triunghiulare a fost îndeplinită.
Exerciții rezolvate
În exercițiile următoare, reprezentați geometric inegalitatea triunghiului sau inegalitatea Minkowski pentru numerele a și b.
Numărul a va fi reprezentat ca un segment pe axa X, originea sa O coincide cu zeroul axei X și celălalt capăt al segmentului (în punctul P) va fi în direcția pozitivă (în dreapta) a Axa X dacă a> 0, dar dacă a < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.
În mod similar, numărul b va fi reprezentat ca un segment a cărui origine este la punctul P. Cealaltă extremă, adică punctul Q va fi în dreapta lui P dacă b este pozitiv (b> 0) și punctul Q va fi | b | unități din stânga lui P dacă b<0.
Exercitiul 1
Graficează inegalitatea triunghiului pentru a = 5 și b = 3 | a + b | ≤ | la | + | b |, fiind c = a + b.
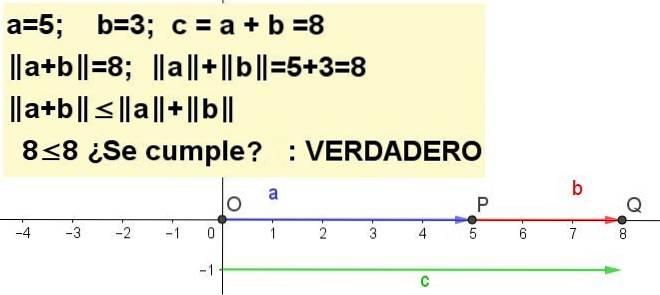
Exercițiul 2
Grafică inegalitatea triunghiulară pentru a = 5 și b = -3.
| a + b | ≤ | la | + | b |, fiind c = a + b.

Exercițiul 3
Arată grafic inegalitatea triunghiului pentru a = -5 și b = 3.
| a + b | ≤ | la | + | b |, fiind c = a + b.
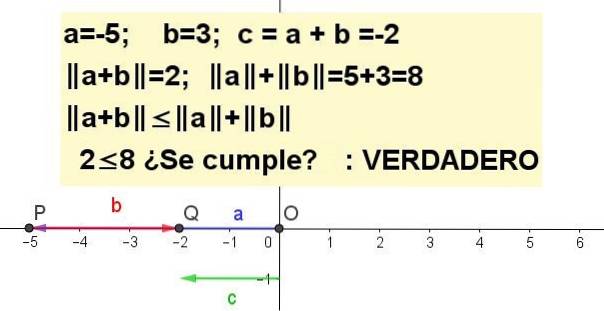
Exercițiul 4
Construiți grafic inegalitatea triunghiulară pentru a = -5 și b = -3.
| a + b | ≤ | la | + | b |, fiind c = a + b.
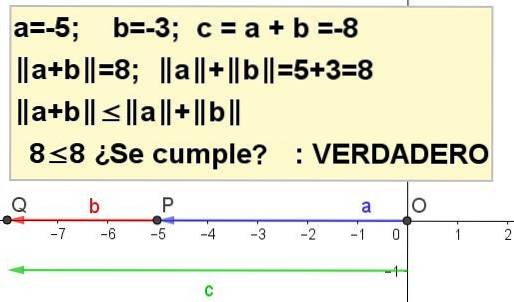
Referințe
- E. Whitesitt. (1980) .Algebra booleană și aplicațiile sale. Companie editorială Continental C. A.
- Mícheál O 'Searcoid. (2003) Elemente de analiză abstractă ... Departamentul de matematică. Colegiul universitar Dublin, Beldfield, Dublind.
- J. Van Wyk. (2006) Matematică și inginerie în informatică. Institutul de Științe și Tehnologie a Calculatoarelor. Biroul Național de Standarde. Washington, D.C. 20234
- Eric Lehman. Matematică pentru informatică. Google Inc.
- F Thomson Leighton (1980). Calcul. Departamentul de Matematică și Laboratorul de Informatică și AI, Institutul de Tehnologie din Massachusetts.
- Academia Khan. Teorema inegalității triunghiului. Recuperat de pe: khanacademy.org
- Wikipedia. Inegalitate triunghiulară. Recuperat din: es. wikipedia.com



Nimeni nu a comentat acest articol încă.