
Dinamica unui sistem de particule exemple, exerciții
dinamica unui sistem de particule Acesta constă în aplicarea legilor de mișcare ale lui Newton asupra unui set de particule, care pot fi discrete (particulele pot fi numărate) sau pot face parte dintr-un obiect extins, în acest caz sistemul este continuu.
Pentru a explica mișcarea unui sistem de particule, este incomod să analizăm fiecare separat și să vedem ce forțe acționează asupra acestuia. În schimb, este definit un punct reprezentativ al setului, numit Centrul de masă.
Descrierea mișcării centrului de masă oferă o imagine de ansamblu foarte precisă asupra mișcării generale a întregului, permite, de asemenea, aplicarea legilor lui Newton într-un mod similar cu atunci când obiectul este considerat ca o particulă adimensională.
Acest ultim model, numit model de particule, Este bine pentru descrierea traducerilor și, de asemenea, atunci când nu trebuie să luați în considerare dimensiunile obiectului. Dar obiectele obișnuite au dimensiuni și dacă au și mișcare de rotație, este necesar să se ia în considerare punctele pe care sunt aplicate forțele.
Indice articol
- 1 Exemple
- 1.1 Pământul și Luna
- 1.2 Obiecte extinse
- 2 Centrul de masă al unui sistem de particule
- Mișcare de 2,1 CM
- 2.2 Forța asupra CM
- 3 Exercițiul a fost rezolvat
- 3.1 Soluția a
- 3.2 Soluția b
- 3.3 Soluția c
- 4 Referințe
Exemple
Pământul și Luna

Un set de particule discrete m1, mDouă, m3... care în cele din urmă se mișcă în ceea ce privește originea unui sistem de coordonate, datorită unei forțe rezultante care acționează asupra lor, este un bun exemplu de sistem de particule.
Pământul poate fi considerat ca o particulă și Luna o altă, apoi ambele constituie un sistem de 2 particule sub acțiunea forței de greutate a Soarelui..
Obiecte extinse
O persoană, un animal sau orice obiect din mediu poate fi, de asemenea, considerat ca un sistem de particule, doar că acestea sunt atât de mici încât nu pot fi numărate pe rând. Acesta este un sistem continuu, dar ținând cont de anumite considerații, tratamentul său este același ca și pentru un sistem discret.
Mai jos sunt detaliile.
Centrul de masă al unui sistem de particule
Pentru a începe studiul unui sistem de particule, trebuie să găsim centrul de masă (CM), care este punctul în care este concentrată toată masa sistemului..
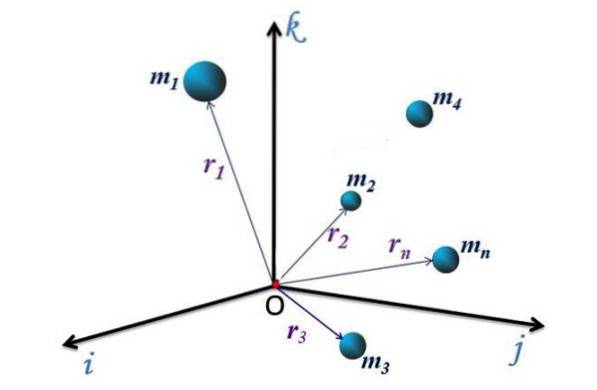
Pentru sistemul discret din Figura 1, cu n particule, fiecare are un vector de poziție îndreptat de la originea O a sistemului de coordonate până la punctul P (x, y, z) unde se află particula. Acești vectori sunt notați ca r1, rDouă, r3... rn.
Coordonatele CM sunt calculate utilizând următoarele ecuații:

Unde fiecare dintre masele mulțimii este reprezentată ca m1, mDouă, m3... mn. Rețineți că suma ∑ meu este egal cu masa totală M a ansamblului. Dacă sistemul este continuu, sumele sunt înlocuite cu integrale.
Fiecare dintre direcțiile perpendiculare este reprezentată de vectorii unitari eu, j Da k, deci, vectorul de poziție al CM, notat rCM, poate fi exprimat prin:
rCM = xCM eu + DaCM j + zCM k
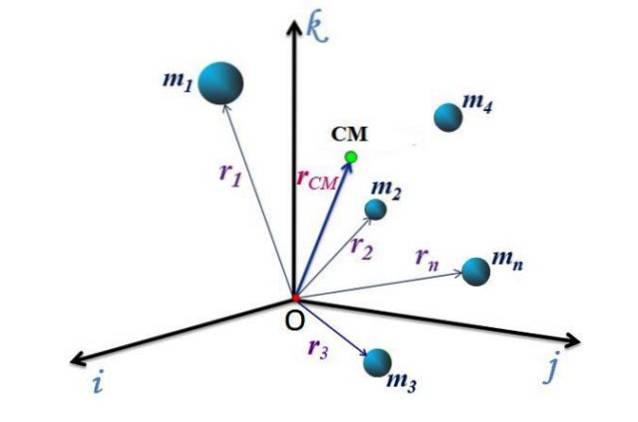
Mișcare CM
Odată ce locația centrului de masă este cunoscută, se aplică ecuațiile de mișcare cunoscute. Viteza CM este prima derivată a poziției în raport cu timpul:

În acest caz, sistemul are un impuls total P care se calculează ca produs al masei totale a sistemului și a vitezei centrului de masă:
P = M ∙vCM
Alternativ, impulsul total al sistemului poate fi calculat direct:
P = m1v1 + mDouăvDouă + m3v3 +…. = ∑ meu veu
În timp ce accelerația CM este derivata vitezei:

Forța asupra CM
Forțele care acționează asupra unui sistem de particule pot fi:
- Forțe interne, datorate interacțiunilor dintre aceleași particule.
- Forțe externe, cauzate de agenți externi sistemului.
Deoarece forțele interne sunt prezentate în perechi, de mărime și direcție egale, dar direcții opuse, conform celei de-a treia legi a lui Newton, este adevărat că:
∑ Fint = 0
Prin urmare, forțele interne nu modifică mișcarea întregului, dar sunt foarte importante pentru a determina energia internă..
Dacă sistemul este izolat și nu există forțe externe, conform primei legi a lui Newton, centrul de masă este în repaus sau se mișcă cu mișcare rectilinie uniformă. În caz contrar, centrul de masă are o accelerare dată de:
∑ Fext = M ∙laCM
Unde M este masa totală a sistemului. Ecuația de mai sus poate fi scrisă astfel:

Și înseamnă că forța externă este echivalentă cu variația temporală a impulsului, un alt mod de a exprima a doua lege a lui Newton și același lucru pe care celebrul fizician englez l-a folosit în cartea sa Principiu.
Exercițiul a fost rezolvat
Centrul de masă al unui sistem cu 2 particule se află pe axa x la un moment dat, în poziția x = 2,0 m și se deplasează cu viteza 5,0 m / s în aceeași direcție și într-o direcție pozitivă. Dacă una dintre particule este la origine și cealaltă, cu masa 0,1 kg, este în repaus la x = 8,0 m, calculați:
a) Masa particulei care se află la origine.
b) Cantitatea de mișcare a sistemului
c) Care este viteza particulei la origine?
Solutie la
Din ecuația pentru poziția centrului de masă:
rCM = xCM eu + DaCM j + zCM k = 2,0 m eu
Deoarece CM are doar o coordonată x, se folosește doar prima ecuație a trio-ului dat anterior:

Acum, coordonatele sunt substituite, dacă particula de la origine este notată cu numărul 1 și cealaltă cu numărul 2, datele numerice sunt:
X1 = 0 m, xDouă = 8,0 m, mDouă = 0,1 kg, xCM = 2,0 m
Rămas:

Soluția b
Cantitatea de mișcare a sistemului este calculată prin:
P = M ∙vCM
Masa totală M este egală cu:
M = 0,3 kg + 0,1 kg = 0,4 kg
Prin urmare:
P = 0,4 kg ∙ 5,0 m / s eu = 2 kg.m / s eu
Soluția c
Din ecuația pentru P a unui sistem cu două particule, se curăță v1, deoarece celelalte date sunt cunoscute, deoarece afirmația spune că particula 2 este în repaus, prin urmare:
vDouă = 0
Da P pur și simplu arată:
P = m1v1
v1 = P / m1 = 2 kg.m / s eu / 0,3 kg = 6,67 m / s eu
Referințe
- Universitatea Duke. Sisteme de particule. Recuperat de la: webhome.phy.duke.edu.
- Rex, A. 2011. Fundamentele fizicii. Pearson.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1. Pearson.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7. Ed. Cengage Learning.
- Tipler, P. (2006) Fizică pentru știință și tehnologie. Ediția a 5-a Volumul 1. Editorial Reverté.



Nimeni nu a comentat acest articol încă.