
Distribuția F caracteristicile și exercițiile rezolvate
F distribuție o Distribuția Fisher-Snedecor este cea utilizată pentru a compara varianțele a două populații diferite sau independente, fiecare dintre acestea urmând o distribuție normală.
Distribuția care urmărește varianța unui set de eșantioane dintr-o singură populație normală este distribuția chi-pătrat (ΧDouă) de grad n-1, dacă fiecare dintre probele din set are n elemente.
Pentru a compara varianțele a două populații diferite, este necesar să se definească un statistic, adică o variabilă auxiliară aleatorie care ne permite să discernem dacă ambele populații au sau nu aceeași varianță.
Respectiva variabilă auxiliară poate fi direct coeficientul varianței eșantionului fiecărei populații, caz în care, dacă respectivul coeficient este apropiat de unitate, există dovezi că ambele populații au varianțe similare.
Indice articol
- 1 Statistica F și distribuția sa teoretică
- 1.1 Media, modul și varianța distribuției F.
- 2 Manipularea distribuției F.
- 2.1 Tabelele distribuției F.
- 2.2 Software pentru distribuția F.
- 3 exerciții rezolvate
- 3.1 Exercițiul 1
- 3.2 Exercițiul 2
- 4 Referințe
Statistica F și distribuția sa teoretică
Statistica variabilă aleatorie F sau F propusă de Ronald Fisher (1890 - 1962) este cea mai frecvent utilizată pentru a compara varianțele a două populații și este definită după cum urmează:
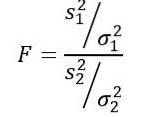
Fiind sDouă varianța eșantionului și σDouă varianța populației. Pentru a distinge fiecare dintre cele două grupuri de populație, se utilizează indicele 1 și respectiv 2..
Se știe că distribuția chi-pătrat cu (n-1) grade de libertate este cea care urmează variabilei auxiliare (sau statistice) definite mai jos:
XDouă = (n-1) sDouă / σDouă.
Prin urmare, statistica F urmează o distribuție teoretică dată de următoarea formulă:
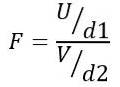
Fiind SAU distribuția chi-pătrat cu d1 = n1 - 1 grade de libertate pentru populația 1 și V distribuția chi-pătrat cu d2 = n2 - 1 grade de libertate pentru populație 2.
Cocientul definit în acest mod este o nouă distribuție de probabilitate, cunoscută sub numele de F distribuție cu d1 grade de libertate în numărător și d2 grade de libertate în numitor.
Media, modul și varianța distribuției F.
Jumătate
Media distribuției F este calculată după cum urmează:
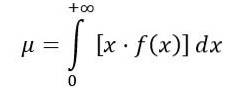
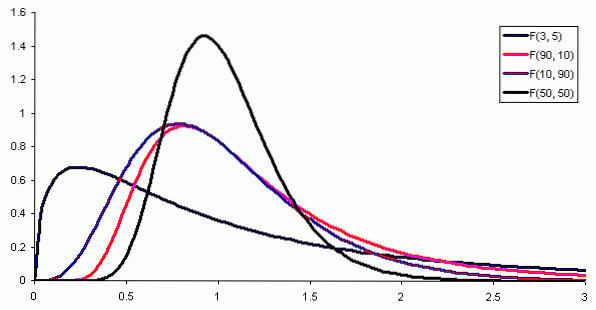
Unde f (x) este densitatea de probabilitate a distribuției F, care este prezentată în figura 1 pentru diferite combinații de parametri sau grade de libertate.
Putem scrie densitatea de probabilitate f (x) ca o funcție a funcției Γ (funcția gamma):
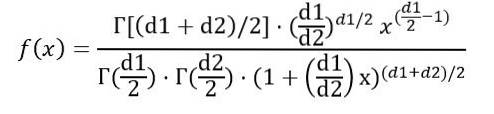
Odată realizată integralul indicat mai sus, se concluzionează că media distribuției F cu grade de libertate (d1, d2) este:
μ = d2 / (d2 - 2) cu d2> 2
În cazul în care se observă că, curios, media nu depinde de gradele de libertate d1 ale numărătorului.
Modă
Pe de altă parte, modul depinde de d1 și d2 și este dat de:
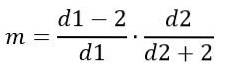
Pentru d1> 2.
Varianța distribuției F.
Varianța σDouă al distribuției F se calculează din integral:
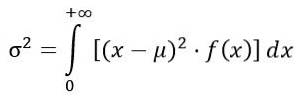
Obținerea:
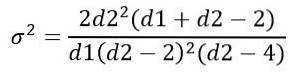
Gestionarea distribuției F.
Ca și alte distribuții de probabilitate continue care implică funcții complicate, gestionarea distribuției F se face folosind tabele sau software..
Tabelele de distribuție F
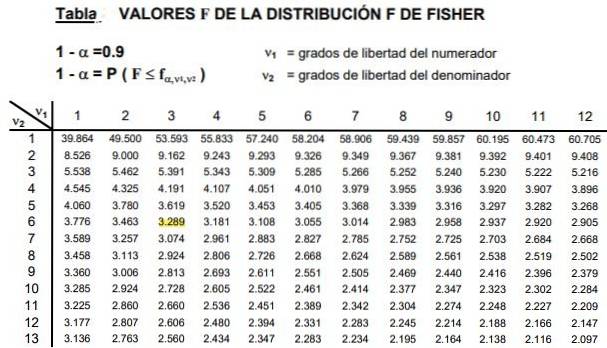
Tabelele implică cei doi parametri sau grade de libertate a distribuției F, coloana indică gradul de libertate al numărătorului și rândul gradul de libertate al numitorului.
Figura 2 prezintă o secțiune a tabelului distribuției F pentru cazul a nivel de semnificație de 10%, adică α = 0,1. Valoarea lui F este evidențiată când d1 = 3 și d2 = 6 cu nivel de încredere 1- α = 0,9 adică 90%.
Software pentru distribuția F.
În ceea ce privește software-ul care gestionează distribuția F, există o mare varietate, de la astfel de foi de calcul excela la pachete specializate precum minitab, SPSS Da R pentru a numi unele dintre cele mai cunoscute.
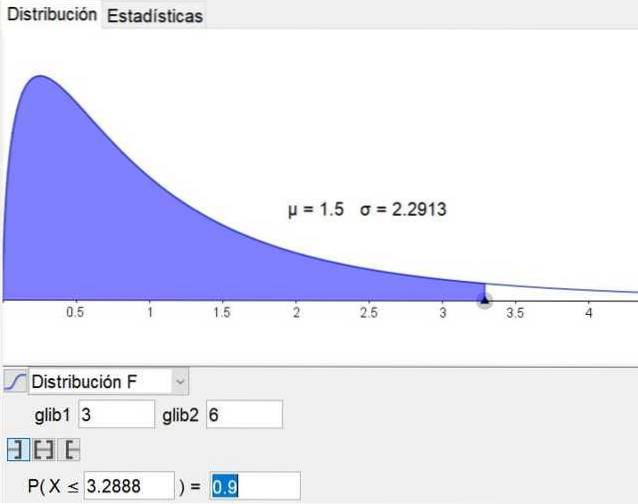
Este de remarcat faptul că software-ul de geometrie și matematică geogebra are un instrument statistic care include principalele distribuții, inclusiv distribuția F. Figura 3 arată distribuția F pentru cazul d1 = 3 și d2 = 6 cu nivel de încredere de 90%.
Exerciții rezolvate
Exercitiul 1
Luați în considerare două eșantioane de populații care au aceeași varianță a populației. Dacă eșantionul 1 are dimensiunea n1 = 5 și eșantionul 2 are dimensiunea n2 = 10, determinați probabilitatea teoretică ca coeficientul varianțelor lor respective să fie mai mic sau egal cu 2.
Soluţie
Trebuie amintit că statistica F este definită ca:
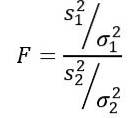
Dar ni se spune că variațiile populației sunt egale, deci pentru acest exercițiu se aplică următoarele:
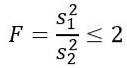
Deoarece vrem să cunoaștem probabilitatea teoretică ca acest coeficient de variații ale eșantionului să fie mai mic sau egal cu 2, trebuie să cunoaștem aria sub distribuția F între 0 și 2, care poate fi obținută prin tabele sau software. Pentru aceasta, trebuie luat în considerare faptul că distribuția F necesară are d1 = n1 - 1 = 5 - 1 = 4 și d2 = n2 - 1 = 10 - 1 = 9, adică distribuția F cu grade de libertate ( 4, 9).
Prin utilizarea instrumentului statistic al geogebra S-a stabilit că această zonă este 0,82, deci se concluzionează că probabilitatea ca coeficientul varianțelor eșantionului să fie mai mic sau egal cu 2 este de 82%.
Exercițiu Două
Există două procese de fabricație pentru foi subțiri. Variabilitatea grosimii trebuie să fie cât mai mică posibil. Din fiecare proces sunt prelevate 21 de probe. Proba din procesul A are o abatere standard de 1,96 microni, în timp ce proba din procesul B are o abatere standard de 2,13 microni. Care dintre procese are cea mai mică variabilitate? Folosiți un nivel de respingere de 5%.
Soluţie
Datele sunt după cum urmează: Sb = 2,13 cu nb = 21; Sa = 1,96 cu na = 21. Aceasta înseamnă că trebuie să lucrăm cu o distribuție F de (20, 20) grade de libertate.
Ipoteza nulă implică faptul că varianța populației ambelor procese este identică, adică σa ^ 2 / σb ^ 2 = 1. Ipoteza alternativă ar implica variații ale populației diferite.
Apoi, sub ipoteza unor varianțe identice ale populației, statistica F calculată este definită ca: Fc = (Sb / Sa) ^ 2.
Deoarece nivelul de respingere a fost luat ca α = 0,05, atunci α / 2 = 0,025
Distribuția F (0,025, 20,20) = 0,406, în timp ce F (0,975, 20,20) = 2,46.
Prin urmare, ipoteza nulă va fi adevărată dacă F calculat îndeplinește: 0,406≤Fc≤2,46. În caz contrar, ipoteza nulă este respinsă.
Ca Fc = (2.13 / 1.96) ^ 2 = 1.18 se concluzionează că statistica Fc se află în intervalul de acceptare a ipotezei nule cu o certitudine de 95%. Cu alte cuvinte, cu o certitudine de 95%, ambele procese de fabricație au aceeași variație a populației..
Referințe
- F Test pentru independență. Recuperat de la: saylordotorg.github.io.
- Med Wave. Statistici aplicate științelor sănătății: testul F. Adus de la: medwave.cl.
- Probabilități și statistici. Distribuție F. Recuperat de pe: probayestadistica.com.
- Triola, M. 2012. Statistici elementare. 11. Ediție. Addison Wesley.
- UNAM. Distribuție F. Recuperat de la: asesorias.cuautitlan2.unam.mx.
- Wikipedia. Distribuție F. Recuperat de pe: es.wikipedia.com



Nimeni nu a comentat acest articol încă.