Formula ecuațiilor de gradul II, modul de rezolvare a acestora, exemple, exerciții

ecuații pătratice sau pătratice și o necunoscută au forma topor^Două + bx + c = 0. Unde a ≠ 0, deoarece dacă ar fi 0, ecuația s-ar transforma într-o ecuație liniară, iar coeficienții a, b și c sunt numere reale.

Necunoscutul care urmează să fie determinat este valoarea lui x. De exemplu, ecuația 3x^Două - 5x + 2 = 0 este o ecuație pătratică completă.

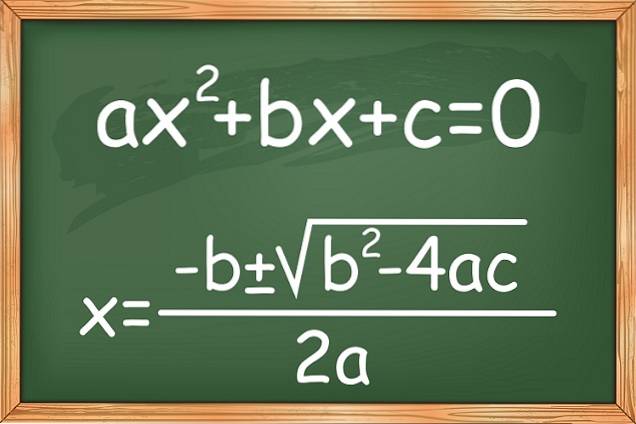
Există, de asemenea, variante cunoscute sub numele de ecuații de gradul II incomplete, cărora le lipsește oricare dintre termeni, cu excepția celui de topor^Două. Aici sunt cateva exemple:

X^Două - 25 = 0

3x^Două - 5x = 0

Al Juarismi, celebrul matematician arab din antichitate, a descris în lucrările sale diferite tipuri de ecuații de gradul I și II, dar numai cu coeficienți pozitivi. Cu toate acestea, matematicianul francez Francois Viete a introdus mai întâi litere pentru a simboliza cantitățile și a propune soluția prin formula hotărât:

Aceasta este o formulă generală care permite rezolvarea unei ecuații pătratice, găsirea rădăcinilor sau a zerourilor sale, chiar dacă soluțiile nu sunt reale. Există și alte modalități de a le rezolva.

Indice articol

• 1 Cum se rezolvă ecuațiile pătratice?
  • 1.1 Rezoluție prin factoring
  • 1.2 Metoda grafică
  • 1.3 Rezoluție cu calculator științific
  • 1.4 Discriminarea unei ecuații pătratice
• 2 Exemple de ecuații pătratice simple
  • 2.1 Ecuația formei x2 + mx + n = 0
  • 2.2 Ecuația incompletă a formei ax2 + c = 0
  • 2.3 Ecuația incompletă a formei ax2 + bx = 0
  • 2.4 Ecuații cu numitor
  • 2.5 Ecuații de ordin superior care devin pătratice
• 3 exerciții simple rezolvate
  • 3.1 - Exercițiul 1
  • 3.2 - Exercițiul 2
  • 3.3 - Exercițiul 3
• 4 Referințe

Cum se rezolvă ecuațiile pătratice?

Ecuațiile de gradul al doilea pot fi rezolvate prin formula dată mai sus și există și alte proceduri algebrice care pot da rezultate în unele ecuații.

Vom rezolva ecuația propusă la început cu formula, o metodă validă pentru orice ecuație pătratică cu o necunoscută:

3x^Două - 5x + 2 = 0

Pentru a utiliza corect formula, observăm că:

• la este coeficientul termenului cu x^Două
• b este coeficientul termenului liniar
• c este termenul independent.

Le vom identifica din aceeași ecuație:

a = 3

b = -5

c = 2

Rețineți că trebuie luat în considerare semnul care însoțește coeficientul. Acum înlocuim aceste valori în formula:

În numărător există simbolul „plus - minus” ±, care indică faptul că cantitatea cu o rădăcină poate fi luată ca pozitivă și, de asemenea, ca negativă. O ecuație pătratică are cel mult două soluții reale, iar acest simbol ia în considerare acest lucru.

Să numim x₁ și x_Două la aceste două soluții, atunci:

X₁ = (5 + 1) / 6 = 1

X_Două = (5-1) / 6 = 4/6 = 2/3

Rezolvare prin factoring

Unele ecuații de gradul al doilea constau în trinomii care sunt ușor de luat în calcul. Dacă da, această metodă este mult mai rapidă. Să luăm în considerare ecuația:

X^Două + 7x - 18 = 0

Factorizarea are această formă:

(x +) ⋅ (x -)

Spațiile goale sunt umplute cu două numere care atunci când sunt înmulțite dau 18, iar când sunt scăzute dau 7. Semnele din paranteze sunt alese cu acest criteriu:

-În prima paranteză semnul este plasat între primul și al doilea termen.

-Iar în a doua paranteză este produsul semnelor care se văd.

În ceea ce privește numerele, acestea sunt ușor marcate în acest caz: sunt 9 și 2. Cel mai mare este întotdeauna plasat în prima dintre paranteze, astfel:

X^Două + 7x - 18 = (x + 9). (x - 2)

Cititorul poate verifica prin intermediul proprietății distributive, că atunci când se dezvoltă produsul din partea dreaptă a egalității se obține trinomul din stânga. Acum ecuația este rescrisă:

(x + 9) ⋅ (x - 2) = 0

Pentru ca egalitatea să fie îndeplinită, este suficient ca unul dintre cei doi factori să fie zero. Deci, în prima trebuie să faci x₁ = -9 sau se poate întâmpla ca al doilea factor să dispară, caz în care x_Două = 2. Acestea sunt soluțiile ecuației.

Metoda grafică

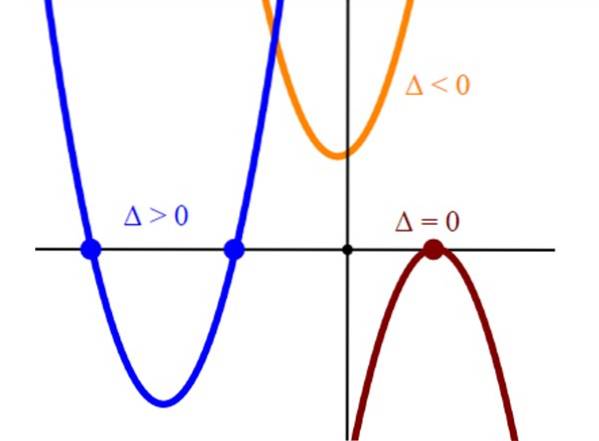
Rădăcinile sau soluțiile ecuației pătratice corespund intersecțiilor parabolei y = topor^Două + bx + c cu axa orizontală sau axa x. Deci, atunci când graficăm parabola corespunzătoare, vom găsi soluția ecuației pătratice făcând y = 0.

Tăieturile parabolelor cu axa orizontală reprezintă soluțiile ecuației topor^Două + bx + c = 0. O parabolă care taie doar axa orizontală într-un singur punct are o singură rădăcină și acesta va fi întotdeauna vârful parabolei.

Și, în cele din urmă, dacă o parabolă nu taie axa orizontală, ecuația corespunzătoare topor^Două + bx + c = 0 lipsește soluții reale.

Construirea unui grafic manual poate fi laborioasă, dar cu ajutorul programelor care graficează online este foarte simplu.

Rezoluție cu calculator științific

Multe modele de calculatoare științifice au opțiunea de a rezolva ecuații pătratice (și alte tipuri de ecuații, de asemenea). Pentru a afla, trebuie să verificați meniul.

Odată aleasă ecuația pătratică a unei opțiuni necunoscute, meniul solicită introducerea valorilor coeficienților a, b și c și returnează soluțiile reale dacă acestea există. Și există, de asemenea, modele de calculatoare științifice care funcționează cu numere complexe și oferă aceste soluții.

Discriminant al unei ecuații pătratice

Pentru a afla dacă ecuația are sau nu soluții reale și câte sunt, fără a fi nevoie să rezolvăm mai întâi, discriminantul Δ este definit ca cantitatea de sub rădăcina pătrată:

Δ = b^Două - 4ac

Conform semnului discriminantului, se știe câte soluții are ecuația în funcție de acest criteriu:

-Două soluții reale: Δ> 0

-O soluție reală (sau două soluții identice): Δ = 0

-Nicio soluție reală: Δ  < 0

De exemplu, câte soluții face ecuația pătratică -7x^Două +12x + 64 = 0? Identificăm coeficienții:

a = -7

b = 12

c = 64

Δ = b^Două - 4ac = 12^Două - 4x (-7) x 64 = 144 + 1792 = 1936> 0

Ecuația are două soluții. Acum să-l vedem pe celălalt:

X^Două - 6x + 9 = 0

a = 1

b = -6

c = 9

Δ = (-6)^Două - 4 x 1 x 9 = 36 - 36 = 0

Aceasta este o ecuație cu o singură soluție sau cu două soluții egale.

Exemple de ecuații pătratice simple

La început am spus că ecuațiile de gradul doi ar putea fi complete dacă trinomul este și incomplete dacă lipsesc termenul liniar sau cel independent. Acum, să ne uităm la anumite tipuri particulare:

Ecuația formei x^Două + mx + n = 0

În acest caz a = 1 și formula se reduce la:

Pentru acest tip de ecuație și întotdeauna în funcție de coeficienții rămași, metoda de factoring poate funcționa bine, așa cum am văzut în secțiunea anterioară.

Ecuația incompletă a formei ax^Două + c = 0

Soluția, dacă există, este de forma:

Există o soluție reală atunci când a sau c au un semn negativ, dar dacă cei doi termeni au același semn, soluția va fi imaginară.

Ecuația incompletă a formei ax^Două + bx = 0

Această ecuație este rezolvată rapid folosind factorizarea, deoarece x este un factor comun în ambii termeni. Una dintre soluții este întotdeauna x = 0, cealaltă se găsește astfel:

topor^Două + bx = 0

x (ax + b) = 0

ax + b = 0 → x = -b / a

Să vedem un exemplu mai jos. Rezolvă:

X^Două - 5x = 0

x (x - 5) = 0

Prin urmare x₁ = 0 și x_Două = 5

Ecuații cu numitor

Există diverse ecuații de tip rațional, în care necunoscutul poate fi prezent atât în ​​numărător, cât și în numitor, sau chiar numai în acesta din urmă, și care prin intermediul manipulărilor algebrice sunt reduse la ecuații pătratice.

Modul de a le rezolva este de a multiplica ambele părți ale egalității cu cel mai mic multiplu comun sau m.c.m al numitorilor și apoi rearanjați termenii. De exemplu:

Ecuații de ordin superior care devin pătratice

Există ecuații de ordin superior care pot fi rezolvate ca și cum ar fi pătrat prin intermediul unei schimbări de variabilă, de exemplu această ecuație bi-pătrat:

X⁴ - 10x^Două + 9 = 0

Fie x^Două = u, atunci ecuația devine:

sau^Două - 10u + 9 = 0

Această ecuație este rezolvată rapid prin factorizare, găsind două numere care s-au înmulțit la 9 și au adăugat 10. Aceste numere sunt 9 și 1:

(u - 9). (u - 1) = 0

Prin urmare, soluțiile acestei ecuații sunt u₁ = 9 și u_Două = 1. Acum returnăm modificarea:

X^Două = 9 → x₁ = 3 și x_Două = -3

X^Două = 1 → x₁ = 1 și x_Două = -1

Ecuația inițială este de ordinul 4, prin urmare are cel puțin 4 rădăcini. Cel din exemplu este -3, -1, 1 și 3.

Exerciții simple rezolvate

- Exercitiul 1

Rezolvați următoarea ecuație pătratică cu necunoscutul în numitor:

Cel mai mic multiplu comun este x (x + 2) și trebuie să multiplicați toți termenii:

Expresia echivalentă rămâne:

5x (x + 2) - x = x (x + 2)

Dezvoltăm:

5x^Două + 10x - x = x^Două + 2x

Toți termenii sunt transpuși în stânga egalității și în dreapta lăsăm 0:

5x^Două + 10x - x - x^Două - 2x = 0

4x^Două - 7x = 0

Factorizăm, deoarece este o ecuație incompletă:

x (4x - 7) = 0

Una dintre soluții este x = 0, cealaltă este:

4x = 7

x = 7/4

- Exercițiul 2

Găsiți soluția ecuațiilor pătratice:

a) -7x^Două +12x + 64 = 0

b) x^Două - 6x + 9 = 0

Solutie la

Din această ecuație știm determinantul Δ, deoarece a fost calculat ca exemplu înainte, așa că vom profita de ea, exprimând astfel formula de rezolvare:

X₁ = (-12 + 44) / -14 = - (32/14) = - (16/7)

X_Două = (-12 - 44) / -14 = 4

Soluția b

Trinomul pătrat x^Două - 6x + 9 este factorizabil, deoarece este un trinom pătrat perfect:

X^Două - 6x + 9 = (x-3)^Două = 0

Soluția acestei ecuații este x = 3.

- Exercițiul 3

Care este ecuația ale cărei soluții sunt 3 și 4?

Soluţie

Expresia factorizată este:

(x - 3) ⋅ (x - 4) = 0

Aplicarea proprietății distributive:

X^Două - 4x -3x + 12 = 0

Cei doi termeni centrali sunt similari și pot fi reduși, lăsând:

X^Două - 7x + 12 = 0

Referințe

1. Baldor. 1977. Algebra elementară. Ediții culturale venezuelene.
2. Hoffman, J. Selecția subiectelor de matematică. Volumul 2.
3. Jiménez, R. 2008. Algebra. Prentice hall.
4. Stewart, J. 2006. Precalcul: Matematică pentru calcul. Al 5-lea. Ediție. Cengage Learning.
5. Zapata, F. 4 moduri de a rezolva o ecuație pătratică. Recuperat de pe: francesphysics.blogspot.com.
6. Zill, D. 1984. Algebră și trigonometrie. Dealul Mcgraw.