
Ecuații polinomiale (cu exerciții rezolvate)

ecuații polinomiale Sunt o afirmație care ridică egalitatea a două expresii sau membri, în care cel puțin unul dintre termenii care alcătuiesc fiecare parte a egalității sunt polinoamele P (x). Aceste ecuații sunt denumite în funcție de gradul variabilelor lor.
În general, o ecuație este o afirmație care stabilește egalitatea a două expresii, în care în cel puțin una dintre acestea există cantități necunoscute, care se numesc variabile sau necunoscute. Deși există multe tipuri de ecuații, ele sunt clasificate în general în două tipuri: algebrică și transcendentală..

Ecuațiile polinomiale conțin doar expresii algebrice, care pot avea una sau mai multe necunoscute implicate în ecuație. În funcție de exponentul (gradul) pe care îl au, acestea pot fi clasificate în: gradul I (liniar), gradul II (pătratic), gradul III (cub), gradul IV (quartic), grad mai mare sau egal cu cinci și irațional.
Indice articol
- 1 Caracteristici
- 2 tipuri
- 2.1 Clasa întâi
- 2.2 Clasa a doua
- 2.3 Solvent
- 2.4 Grad major
- 3 exerciții rezolvate
- 3.1 Primul exercițiu
- 3.2 Al doilea exercițiu
- 4 Referințe
Caracteristici
Ecuațiile polinomiale sunt expresii care sunt formate dintr-o egalitate între două polinoame; adică prin sumele finite ale înmulțirilor între valori necunoscute (variabile) și numere fixe (coeficienți), unde variabilele pot avea exponenți, iar valoarea lor poate fi un număr întreg pozitiv, inclusiv zero.
Exponenții determină gradul sau tipul de ecuație. Termenul expresiei care are cel mai mare exponent valoric va reprezenta gradul absolut al polinomului.
Ecuațiile polinomiale sunt, de asemenea, cunoscute sub numele de algebră, coeficienții lor pot fi numere reale sau complexe, iar variabilele sunt numere necunoscute reprezentate printr-o literă, cum ar fi: "x".
Dacă înlocuind o valoare cu variabila "x" în P (x) rezultatul este egal cu zero (0), atunci se spune că respectiva valoare satisface ecuația (este o soluție) și se numește în general rădăcina polinomului.
Când dezvoltați o ecuație polinomială, doriți să găsiți toate rădăcinile sau soluțiile.
Tipuri
Există mai multe tipuri de ecuații polinomiale, care se diferențiază în funcție de numărul de variabile și, de asemenea, în funcție de gradul exponentului lor.
Astfel, ecuațiile polinomiale - unde primul său termen este un polinom care are o singură necunoscută, având în vedere că gradul său poate fi orice număr natural (n) și al doilea termen este zero -, poate fi exprimat după cum urmează:
lan * Xn + lan-1 * Xn-1 +… + A1 * X1 + la0 * X0 = 0
Unde:
- lan, lan-1 deja0, sunt coeficienți reali (numere).
- lan este diferit de zero.
- Exponentul n este un număr întreg pozitiv care reprezintă gradul ecuației.
- x este variabila sau necunoscutul care trebuie căutat.
Gradul absolut sau mai mare al unei ecuații polinomiale este exponentul cu cea mai mare valoare dintre toți cei care formează polinomul; astfel, ecuațiile sunt clasificate ca:
Clasa întâi
Ecuațiile polinomiale de gradul I, cunoscute și sub numele de ecuații liniare, sunt acelea în care gradul (cel mai mare exponent) este egal cu 1, polinomul este de forma P (x) = 0; și este compus dintr-un termen liniar și unul independent. Este scris după cum urmează:
ax + b = 0.
Unde:
- a și b sunt numere reale și a ≠ 0.
- ax este termenul liniar.
- b este termenul independent.
De exemplu, ecuația 13x - 18 = 4x.
Pentru a rezolva ecuații liniare, toți termenii care conțin x-ul necunoscut trebuie să fie trecuți pe o parte a egalității, iar cei care nu o au se mută pe cealaltă parte, pentru a o rezolva și a obține o soluție:
13x - 18 = 4x
13x = 4x + 18
13x - 4x = 18
9x = 18
x = 18 ÷ 9
x = 2.
Astfel, ecuația dată are o singură soluție sau rădăcină, care este x = 2.
Clasa a doua
Ecuațiile polinomiale de gradul II, cunoscute și sub numele de ecuații pătratice, sunt acelea în care gradul (cel mai mare exponent) este egal cu 2, polinomul este de forma P (x) = 0 și este compus dintr-un termen pătratic, unul liniar și unul independent. Se exprimă după cum urmează:
toporDouă + bx + c = 0.
Unde:
- a, b și c sunt numere reale și a ≠ 0.
- toporDouă este termenul pătratic și „a” este coeficientul termenului pătratic.
- bx este termenul liniar, iar "b" este coeficientul termenului liniar.
- c este termenul independent.
Solvent
În general, soluția la acest tip de ecuații este dată de rezolvarea x din ecuație și este următoarea, care se numește rezolvată:

Acolo, (bDouă - 4ac) se numește discriminantul ecuației și această expresie determină numărul de soluții pe care le poate avea ecuația:
- Da (bDouă - 4ac) = 0, ecuația va avea o singură soluție care este dublă; adică va avea două soluții egale.
- Da (bDouă - 4ac)> 0, ecuația va avea două soluții reale diferite.
- Da (bDouă - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).
De exemplu, avem ecuația 4xDouă + 10x - 6 = 0, pentru a-l rezolva identificați mai întâi termenii a, b și c, apoi înlocuiți-l în formula:
a = 4
b = 10
c = -6.
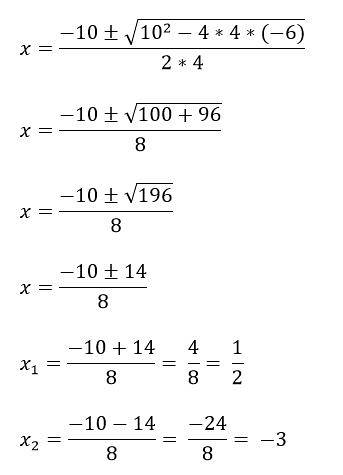
Există cazuri în care ecuațiile polinomiale de gradul al doilea nu au toți cei trei termeni și de aceea sunt rezolvate într-un mod diferit:
- În cazul în care ecuațiile pătratice nu au termenul liniar (adică b = 0), ecuația va fi exprimată ca axDouă + c = 0. Pentru a o rezolva, rezolva pentru xDouă iar rădăcinile pătrate se aplică fiecărui membru, reținând că trebuie luate în considerare cele două semne posibile pe care le poate avea necunoscutul:
toporDouă + c = 0.
XDouă = - c ÷ a
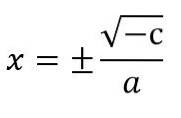
De exemplu, 5 xDouă - 20 = 0.
5 xDouă = 20
XDouă = 20 ÷ 5
x = ± √4
x = ± 2
X1 = 2.
XDouă = -2.
- Când ecuația pătratică nu are un termen independent (adică c = 0), ecuația va fi exprimată ca axDouă + bx = 0. Pentru a o rezolva, trebuie să luăm factorul comun al necunoscutului x în primul membru; Deoarece ecuația este egală cu zero, este adevărat că cel puțin unul dintre factori va fi egal cu 0:
toporDouă + bx = 0.
x (ax + b) = 0.
Astfel, trebuie să:
x = 0.
x = -b ÷ a.
De exemplu: avem ecuația 5xDouă + 30x = 0. Primul factor:
5xDouă + 30x = 0
x (5x + 30) = 0.
Se generează doi factori care sunt x și (5x + 30). Se consideră că una dintre acestea va fi egală cu zero, iar celeilalte vor primi o soluție:
X1 = 0.
5x + 30 = 0
5x = -30
x = -30 ÷ 5
XDouă = -6.
Cea mai înaltă notă
Ecuațiile polinomiale de grad superior sunt acelea care merg de la gradul al treilea, care pot fi exprimate sau rezolvate cu ecuația polinomială generală pentru orice grad:
lan * Xn + lan-1 * Xn-1 +… + A1 * X1 + la0 * X0 = 0
Acest lucru este utilizat deoarece o ecuație cu un grad mai mare de doi este rezultatul factorizării unui polinom; adică este exprimată ca multiplicarea polinoamelor de gradul unu sau mai mare, dar fără rădăcini reale.
Soluția acestui tip de ecuații este directă, deoarece multiplicarea a doi factori va fi egală cu zero dacă oricare dintre factori este nul (0); Prin urmare, fiecare dintre ecuațiile polinomiale găsite trebuie rezolvate, stabilind fiecare dintre factorii săi egali cu zero.
De exemplu, avem ecuația de gradul al treilea (cub) x3 + XDouă +4x + 4 = 0. Pentru a o rezolva, trebuie parcurși următorii pași:
- Termenii sunt grupați:
X3 + XDouă +4x + 4 = 0
(X3 + XDouă ) + (4x + 4) = 0.
- Membrii sunt descompuși pentru a obține factorul comun al necunoscutului:
XDouă (x + 1) + 4 (x + 1) = 0
(XDouă + 4)*(x + 1) = 0.
- În acest fel, se obțin doi factori, care trebuie să fie egali cu zero:
(XDouă + 4) = 0
(x + 1) = 0.
- Se poate observa că factorul (xDouă + 4) = 0 nu va avea o soluție reală, în timp ce factorul (x + 1) = 0 va avea. Deci soluția este:
(x + 1) = 0
x = -1.
Exerciții rezolvate
Rezolvați următoarele ecuații:
Primul exercițiu
(2xDouă + 5)*(x - 3)*(1 + x) = 0.
Soluţie
În acest caz, ecuația este exprimată ca înmulțirea polinoamelor; adică este luată în calcul. Pentru a-l rezolva, fiecare factor trebuie setat egal cu zero:
- 2xDouă + 5 = 0, nu are nicio soluție.
- x - 3 = 0
- x = 3.
- 1 + x = 0
- x = - 1.
Astfel, ecuația dată are două soluții: x = 3 și x = -1.
Al doilea exercițiu
X4 - 36 = 0.
Soluţie
A fost dat un polinom, care poate fi rescris ca o diferență de pătrate pentru a ajunge la o soluție mai rapidă. Astfel, ecuația este:
(XDouă + 6)*(XDouă - 6) = 0.
Pentru a găsi soluția ecuațiilor, ambii factori sunt setați la zero:
(XDouă + 6) = 0, nu are nicio soluție.
(XDouă - 6) = 0
XDouă = 6
x = ± √6.
Astfel, ecuația inițială are două soluții:
x = √6.
x = - √6.
Referințe
- Andres, T. (2010). Olimpiada matematică Tresure. Springer. New York.
- Angel, A. R. (2007). Algebra elementară. Pearson Education,.
- Baer, R. (2012). Algebră liniară și geometrie proiectivă. Courier Corporation.
- Baldor, A. (1941). Algebră. Havana: Cultură.
- Castaño, H. F. (2005). Matematică înainte de calcul. Universitatea din Medellin.
- Cristóbal Sánchez, M. R. (2000). Manual de pregătire olimpică pentru matematică. Universitatea Jaume I.
- Kreemly Pérez, M. L. (1984). Algebra superioară I.
- Massara, N. C.-L. (o mie noua sute nouazeci si cinci). Matematică 3.



Nimeni nu a comentat acest articol încă.