factorul de compresibilitate Z, sau factorul de compresie pentru gaze, este o valoare adimensională (fără unități) care este introdusă ca o corecție în ecuația stării gazelor ideale. În acest fel, modelul matematic seamănă mai mult cu comportamentul observat al gazului..
În gazul ideal, ecuația de stare care se referă la variabilele P (presiune), V (volum) și T (temperatură) este: P.V ideal = n.R.T cu n = numărul de moli și R = constanta ideală a gazului. Adăugând corecția pentru factorul de compresibilitate Z, această ecuație devine:
P.V = Z.n.R.T
Indice articol
Ținând cont că volumul molar este Vmisto = V / n, avem volumul molar real:
P . Vreal = Z. R. T → Z = PV real/ RT
Deoarece factorul de compresibilitate Z depinde de condițiile gazului, acesta este exprimat în funcție de presiune și temperatură:
Z = Z (P, T)
Comparând primele două ecuații, se poate observa că, dacă numărul de moli n este egal cu 1, volumul molar al unui gaz real este legat de cel al gazului ideal prin:
Vreal / Videal = Z → V real = Z Videal
Când presiunea depășește 3 atmosfere, majoritatea gazelor încetează să se mai comporte ca gaze ideale, iar volumul real diferă semnificativ de cel ideal.
Acest lucru a fost realizat în experimentele sale de către fizicianul olandez Johannes Van der Waals (1837-1923), care l-a determinat să creeze un model care să fie mai potrivit pentru rezultate practice decât ecuația ideală a gazului: ecuația Van de stat..
Conform ecuației P.Vreal= Z.n.RT, Pentru un gaz ideal, Z = 1. Cu toate acestea, în gazele reale, odată cu creșterea presiunii, crește și valoarea lui Z. Acest lucru are sens, deoarece cu cât presiunea este mai mare, moleculele de gaz au mai multe oportunități de a se ciocni, prin urmare forțele de respingere cresc și odată cu acesta volumul.
Pe de altă parte, la presiuni mai mici, moleculele se mișcă mai liber și forțele de respingere scad. Prin urmare, este de așteptat un volum mai mic. În ceea ce privește temperatura, atunci când crește, Z scade.
După cum a observat Van der Waals, în vecinătatea așa-numitului punct critic, comportamentul gazului se abate foarte mult de cel al unui gaz ideal..
Punctul critic (Tc, Pc) ale oricărei substanțe sunt valorile presiunii și temperaturii care determină comportamentul acesteia înainte de o schimbare de fază:
-Tc este temperatura peste care gazul în cauză nu lichefiază.
-Pc este presiunea minimă necesară pentru lichefierea gazului la temperatura Tc
Fiecare gaz are propriul său punct critic, cu toate acestea, definind temperatura și presiunea redusă Tr Și pr după cum urmează:
Pr = P / Pc
Vr = V / Vc
Tr = T / Tc
Se observă că un gaz limitat cu același Vr Da Tr exercită aceeași presiune Pr. Din acest motiv, dacă Z este reprezentat grafic în funcție de Pr către sine Tr, fiecare punct de pe acea curbă este același pentru orice gaz. Aceasta se numește principiul stărilor corespunzătoare.
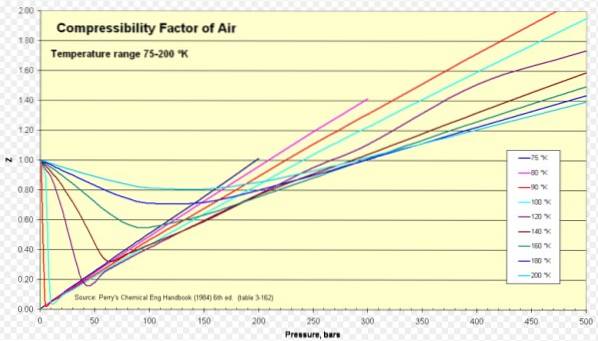
Mai jos este o curbă de compresibilitate pentru diferite gaze la diferite temperaturi reduse. Iată câteva exemple de Z pentru unele gaze și o procedură pentru a găsi Z folosind curba.
Gazele ideale au Z = 1, după cum sa explicat la început.
Pentru aerul Z este de aproximativ 1 într-o gamă largă de temperaturi și presiuni (a se vedea figura 1), unde modelul ideal de gaz oferă rezultate foarte bune.
Z> 1 pentru toate presiunile.
Pentru a găsi Z pentru apă, aveți nevoie de valorile punctelor critice. Punctul critic al apei este: Pc = 22,09 MPa și Tc= 374,14 ° C (647,3 K). Din nou, trebuie luat în considerare faptul că factorul de compresibilitate Z depinde de temperatură și presiune..
De exemplu, să presupunem că doriți să găsiți Z de apă la 500 ° C și 12 MPa. Apoi, primul lucru de făcut este să calculați temperatura redusă, pentru care gradele Celsius trebuie convertite în Kelvin: 50 ° C = 773 K:
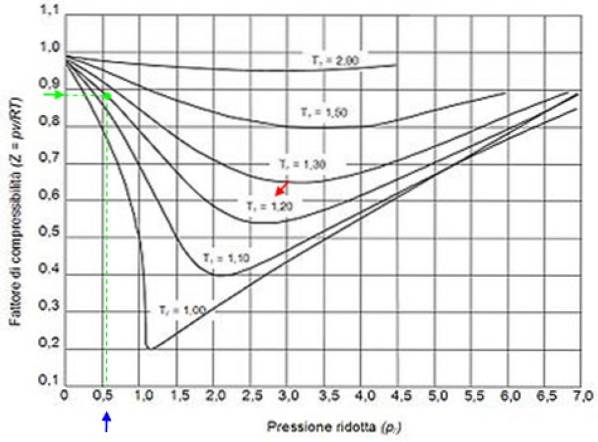
Tr = 773 / 647,3 = 1,2
Pr = 12 / 22,09 = 0,54
Cu aceste valori plasăm în graficul cifrei curba corespunzătoare lui Tr = 1,2, indicat printr-o săgeată roșie. În continuare, căutăm valoarea lui P pe axa orizontalăr mai aproape de 0,54, marcat cu albastru. Acum trasăm o verticală până când interceptăm curba Tr = 1.2 și în cele din urmă este proiectat din acel punct către axa verticală, unde citim valoarea aproximativă a lui Z = 0.89.
Există o probă de gaz la o temperatură de 350 K și o presiune de 12 atmosfere, cu un volum molar cu 12% mai mare decât cel prezis de legea ideală a gazelor. Calculati:
a) Factorul de compresie Z.
b) Volumul molar de gaz.
c) Conform rezultatelor anterioare, indicați care sunt forțele dominante din acest eșantion de gaze.
Date: R = 0,082 L.atm / mol.K
Știind că V real este cu 12% mai mare decât Videal :
Vreal = 1,12Videal
Z = V real / Videal = 1,12
P. Vreal = Z. R. T → Vreal = (1,12 x 0,082 x 350/12) L / mol = 2,14 L / mol.
Forțele respingătoare sunt cele care predomină, deoarece volumul eșantionului a crescut.
Există 10 moli de etan confinați într-un volum de 4,86 L la 27 ° C. Găsiți presiunea exercitată de etan de la:
a) Modelul ideal de gaz
b) Ecuația van der Waals
c) Găsiți factorul de compresie din rezultatele anterioare.
Date pentru etan
Coeficienții Van der Waals:
a = 5.489 dm6. ATM. cârtiță-Două și b = 0,06380 dm3. cârtiță-1.
Presiune critică: 49 atm. Temperatura critică: 305 K
Temperatura este trecută la kelvin: 27 º C = 27 +273 K = 300 K, de asemenea, amintiți-vă că 1 litru = 1 L = 1 dm3.
Apoi datele furnizate sunt înlocuite în ecuația gazului ideal:
P.V = n.R.T → P = (10 x 0,082 x 300 / 4,86 L) atm = 50,6 atm
Ecuația de stare Van der Waals este:
Unde a și b sunt coeficienții dați de enunț. Când curățați P:
Calculăm presiunea și temperatura reduse:
Pr = 35,2 / 49 = 0,72
Tr = 300/305 = 0,98 ≈ 1
Cu aceste valori căutăm valoarea lui Z în graficul din figura 2, constatând că Z este aproximativ 0,7.
Nimeni nu a comentat acest articol încă.