
Rezultă forța modul în care este calculată și exercițiile rezolvate
forta rezultând este suma tuturor forțelor care acționează asupra aceluiași corp. Când un corp sau obiect este supus acțiunii mai multor forțe simultan, are loc un efect. Forțele de acționare pot fi înlocuite cu o singură forță care produce același efect. Această forță unică este forța rezultată cunoscută și sub numele de forță netă și este reprezentată de simbol FR .
Efectul pe care îl produce FR va depinde de mărimea, direcția și simțul său. Mărimile fizice care au direcție și sens sunt mărimi vectoriale.
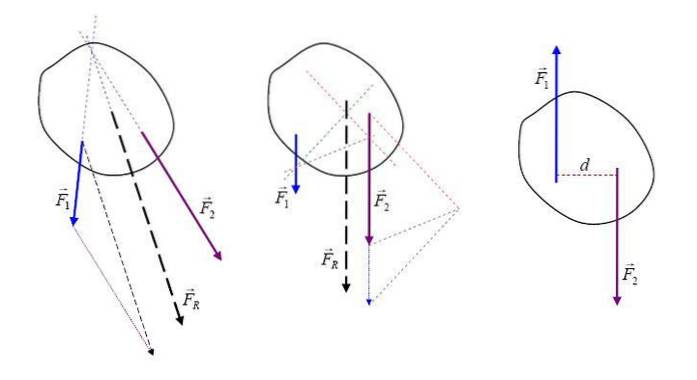
Fiind forțele care acționează asupra mărimilor vectoriale ale corpului, forța rezultată FR este o sumă vectorială a tuturor forțelor și poate fi reprezentată grafic cu o săgeată care indică direcția și direcția sa.
Cu forța rezultată, problema unui corp afectat de mai multe forțe este simplificată prin reducerea acestuia la o singură forță care acționează.
Indice articol
- 1 Formula
- 2 Cum calculați forța rezultată?
- 2.1 rezultat al forțelor paralele
- 2.2 Forțe neparalele
- 3 exerciții rezolvate
- 4 Referințe
Formulă
Reprezentarea matematică a forței rezultate este o însumare vectorială a forțelor.
FR= ∑F (1)
∑F = F1+ FDouă+ F3+... FN (Două)
FR= Forța rezultată
∑F = Suma forțelor
N= Număr de forțe
Forța rezultantă poate fi reprezentată și de ecuația legii a lui Newton.
FR= m.la (3)
m= masa corporală
a = accelerarea corpului
Dacă ecuația (1) este substituită în ecuația (3), se obțin următoarele ecuații:
∑F = m.la (4)
F1+ FDouă+ F3+... FN = m.la (5)
Expresiile matematice (4) și (5) oferă informații despre starea corpului prin obținerea vectorului de accelerație la.
Cum calculați forța rezultată?
Forța rezultată este obținută prin aplicarea celei de-a doua legi a lui Newton care prevede următoarele:
Forța netă care acționează asupra unui corp este egală cu produsul masei sale și cu accelerația pe care o dobândește. (Ecuația (3))
Accelerarea corpului va avea direcția forței nete aplicate. Dacă toate forțele care acționează asupra corpului sunt cunoscute, ar fi suficient să le adăugați vectorial pentru a obține forța rezultată. La fel, dacă se cunoaște forța rezultantă, ar fi suficient să o împărțim la masa corpului pentru a obține accelerația sa.
Dacă forța rezultată este zero, corpul este în repaus sau la viteză constantă. Dacă o singură forță acționează asupra corpului, forța rezultată este egală cu acea forță FR=F.
Când mai multe forțe acționează asupra aceluiași corp, trebuie luate în considerare componentele vectoriale ale forței și dacă aceste forțe sunt sau nu paralele.
De exemplu, dacă alunecăm orizontal o carte așezată pe o masă, forțele în direcția orizontală sunt singurele care oferă accelerație corpului. Forța verticală netă pe carte este zero.
Dacă forța aplicată cărții are o înclinație față de planul orizontal al mesei, forța este scrisă în funcție de componentele verticale și orizontale.
Rezultând forțe paralele
Forțele paralele care acționează asupra unui corp sunt acele forțe care acționează în aceeași direcție. Ele pot fi de două tipuri cu sens egal sau opus.
Când forțele care acționează asupra unui corp au aceeași direcție și aceeași direcție sau sunt în direcția opusă, forța rezultată se obține prin efectuarea sumei algebrice a valorilor numerice ale forțelor.
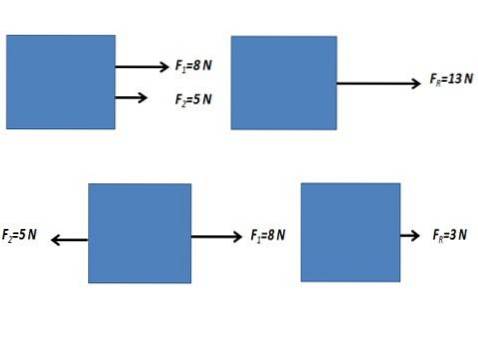
Forțe non-paralele
Atunci când forțele non-paralele sunt aplicate unui corp, rezultanta forțelor va avea componente dreptunghiulare și verticale. Expresia matematică pentru calcularea forței nete este:
FRDouă= (∑ FX)Două+(∑ FDa)Două (6)
asa de θX= ∑ FDa / ∑ FX (7)
∑ FX și ∑ FX= Sumarea algebrică a componentelor X și Da a forțelor aplicate
θX= unghiul format de forța rezultantă FR cu arbore X
Rețineți că forța de expresie rezultată (6) nu este evidențiată cu caractere aldine și se datorează faptului că exprimă doar valoarea numerică. Direcția este determinată de unghi θX.
Expresia (6) este valabilă pentru forțele care acționează în același plan. Când forțele acționează în spațiu, se ia în considerare componenta z de forță atunci când se lucrează cu componente dreptunghiulare.
Exerciții rezolvate
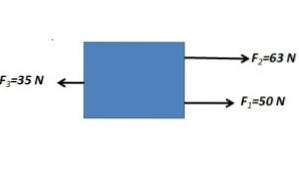
Forțele paralele în aceeași direcție sunt adăugate și scăzute cu forța paralelă în direcția opusă
FR= 63 N + 50 N - 35 N = 78N
Forța rezultată are o magnitudine de 78N cu direcție orizontală.
2. Calculați forța rezultată a unui corp sub influența a două forțe F1 Da FDouă. Forta F1 are o magnitudine de 70N și se aplică orizontal. Forta FDouă are o magnitudine de 40N și se aplică la un unghi de 30 ° față de planul orizontal.
Pentru a rezolva acest exercițiu, este desenată o diagramă a corpului liber cu axele de coordonate X și Da
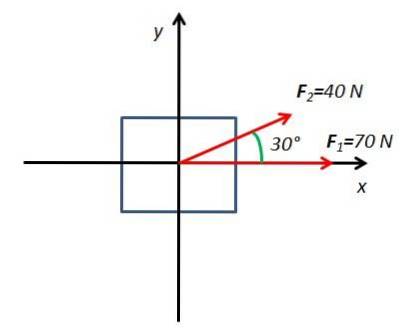
Toate componentele sunt determinate X și Da a forțelor care acționează asupra corpului. Forta F1 are o singură componentă orizontală pe axă X. Forta FDouă are două componente F2x și F2 și care se obțin din funcțiile sinus și cosinus ale unghiului 30 °.
F1x = F1=70N
F2x = FDouă cos 30 ° = 40 N.cos 30 ° = 34,64N
F1y = 0
F2 și= FDouă fără 30 ° = 40 fără 30 ° = 20N
∑ FX =70N + 34,64N = 104,64N
∑ FDa=20N + 0 = 20N
Odată ce forțele rezultate în arbore au fost determinate X și Da procedăm la obținerea valorii numerice a forței rezultante.
FRDouă= (∑ FX)Două+(∑ FDa)Două
Forța rezultată este rădăcina pătrată a sumei componentelor pătrate ale forțelor
FR= √ (104.64N)Două+(20N)Două
FR= 106,53N
Unghiul format de forța rezultantă FR se obține din următoarea expresie:
θX= așa-1(∑ FDa / ∑ FX)
θX= asa de-1(20N / 104,64N) = 10,82 °
Forța rezultată FR are o magnitudine de 106,53N și are o direcție determinată de unghiul de 10,82 ° pe care îl formează cu orizontală.
Referințe
- Dola, G, Duffy, M și Percival, A. Fizică. Spania: Heinemann, 2003.
- Avison, J H. Lumea Fizicii. India: Thomas Nelson și Sons, 1989.
- Pinsent, M. Procese fizice. Regatul Unit: Nelson Thomas, 2002.
- Yadav, S K. Inginerie mecanică. Delhi: Editura Discovery, 2006.
- Serway, R A și Jewett, J W. Fizica pentru oamenii de știință și ingineri. California, SUA: Brooks / Cole, 2010.



Nimeni nu a comentat acest articol încă.