
Legea lui Gauss

Care este legea lui Gauss?
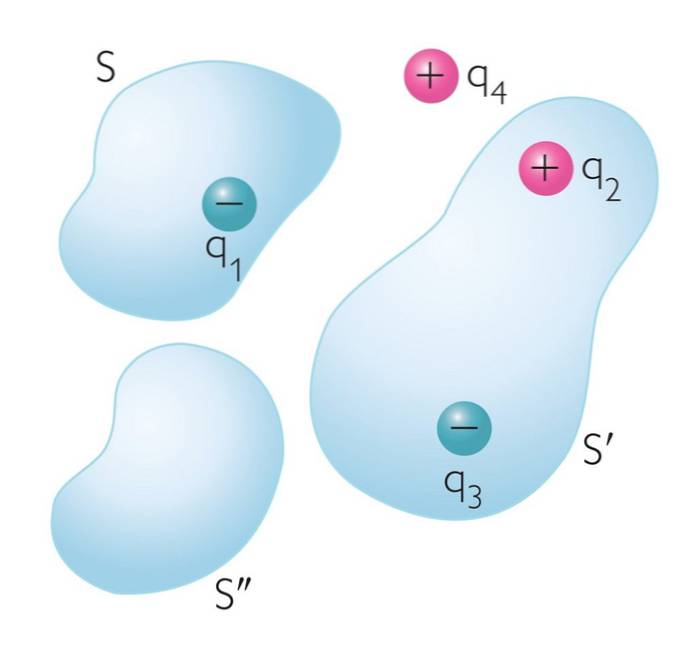
legea lui Gauss stabilește că fluxul de câmp electric printr-o suprafață închisă imaginară este proporțional cu valoarea de încărcare netă a particulelor găsite în interiorul suprafeței respective.
Denotând fluxul electric printr-o suprafață închisă ca ΦȘI și taxa netă închisă de suprafață de Îenc, atunci se stabilește următoarea relație matematică:
ΦȘI = c ∙ Qenc
Unde c este constanta proporționalității.
Explicația legii lui Gauss
Pentru a înțelege semnificația legii lui Gauss, este necesar să se explice conceptele implicate în enunțul său: sarcina electrică, câmpul electric și câmpul electric curg printr-o suprafață..
Incarcare electrica
Încărcarea electrică este una dintre proprietățile fundamentale ale materiei. Un obiect încărcat poate avea unul din cele două tipuri de sarcină: pozitivă sau negativă, deși în mod normal obiectele sunt neutre, adică au aceeași cantitate de sarcină negativă ca pozitivă..
Două obiecte încărcate de același tip se resping reciproc chiar și atunci când nu există contact între ele și sunt în vid. Dimpotrivă, când fiecare dintre corpuri are sarcini de un semn diferit, atunci se atrag reciproc. Acest tip de interacțiune la distanță este cunoscut sub numele de interacțiune electrică..
În sistemul internațional al unităților SI, sarcina electrică este măsurată în culombi (C). Purtătorul de sarcină elementară negativ este electron cu încărcare de -1,6 x 10-19C iar purtătorul de sarcină elementară pozitivă este protonul cu o valoare de încărcare +1,6 x 10-19C. De obicei, corpurile încărcate au între 10-9C Da 10-3C.
câmp electric
Un corp încărcat electric modifică spațiul din mediul său, umplându-l cu ceva invizibil numit câmp electric. Pentru a ști că acest câmp este prezent necesită o încărcare pozitivă a punctului de testare.
Dacă sarcina de testare este plasată într-un loc în care există un câmp electric, apare o forță pe el într-o anumită direcție, care este aceeași cu cea a câmpului electric. Intensitatea câmpului este forța asupra sarcinii de test împărțită la cantitatea de sarcină pe sarcina de test. Apoi unitățile câmpului electric ȘI în Sistemul Internațional de unități sunt Newton Intra coulomb: [E] = N / C.
Încărcăturile punct pozitive produc un câmp radial spre exterior, în timp ce încărcările negative produc un câmp radial spre interior. Mai mult, câmpul produs de o sarcină punctuală se descompune odată cu inversarea pătratului distanței până la sarcina respectivă.
Linii de câmp electric
Michael Faraday (1791 - 1867) a fost primul care a avut o imagine mentală a câmpului electric, imaginându-l ca linii care urmează direcția câmpului. În cazul unei sarcini punctuale pozitive, aceste linii sunt radiale începând de la centru spre exterior. În cazul în care liniile sunt mai apropiate, câmpul este mai intens și mai puțin intens acolo unde sunt mai departe.
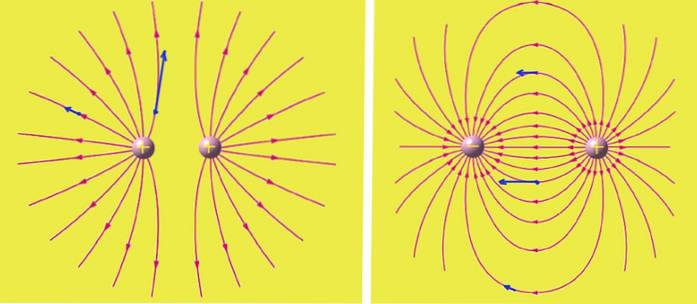
Sarcinile pozitive sunt sursele din care ies liniile de câmp electric, în timp ce sarcinile negative sunt chiuvetele liniilor..
Liniile de câmp electric nu se închid în ele însele. Într-un set de încărcături liniile părăsesc încărcăturile pozitive și intră pe cele pozitive, dar pot ajunge sau proveni din infinit.
De asemenea, ele nu se intersectează și în fiecare punct al spațiului vectorul câmpului electric este tangent la linia câmpului și proporțional cu densitatea liniilor de acolo..

Fluxul câmpului electric
Liniile de câmp electric seamănă cu curgerile unui râu care curge ușor, de unde s-a născut conceptul de curgere a câmpului electric..
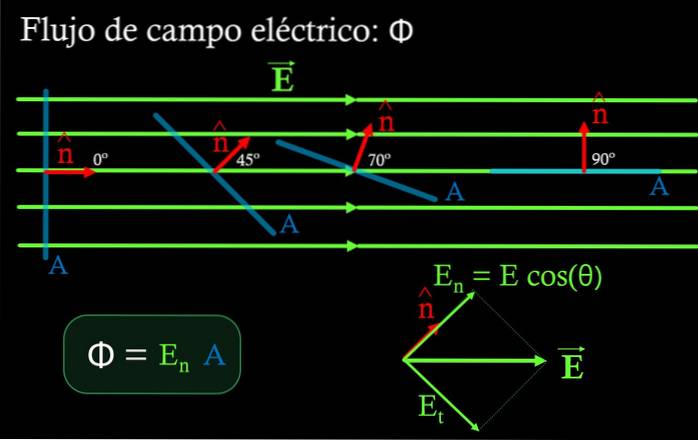
Într-o regiune în care câmpul electric este uniform, fluxul Φ printr-o suprafață plană este produsul componentei normale a câmpului En la această suprafață, înmulțită cu suprafața LA De acelasi:
Φ = En ∙ A
Componenta En se obține prin înmulțirea magnitudinii câmpului electric cu cosinusul unghiului format între câmp și vectorul normal al unității la suprafața LA. (vezi figura 4).
Cererile legii lui Gauss
Legea lui Gauss poate fi aplicată pentru a determina câmpul electric produs de distribuțiile de sarcină cu un grad ridicat de simetrie.
Câmpul electric al unei sarcini punctuale
O încărcare punctuală produce un câmp electric radial care este expediat dacă sarcina este pozitivă și intră altfel..
Alegând ca suprafață gaussiană o sferă imaginară de rază R și concentrică la sarcina Q, în toate punctele de pe suprafața sferei menționate câmpul electric este de aceeași magnitudine și direcția sa este întotdeauna normală la suprafață. Deci, în acest caz fluxul câmpului electric este produsul mărimii câmpului și a suprafeței totale a suprafeței sferice:
Φ = E ∙ A = E ∙ 4πRDouă
Pe de altă parte, legea lui Gauss afirmă că: Φ = c ∙ Q, fiind constanta proporționalității c. Când lucrați în unități ale sistemului internațional de măsurare, constanta c este inversul permitivității vidului, iar legea lui Gauss este formulată astfel:
Φ = (1 / εsau) ∙ Î
Încorporând rezultatul obținut pentru fluxul către legea lui Gauss, avem:
E ∙ 4πRDouă = (1 / εsau) ∙ Î
Și pentru amploarea ȘI rezultat:
E = (1 / 4πεsau) ∙ (Q / RDouă)
Ceea ce este pe deplin de acord cu legea lui Coulomb a câmpului electric al unei sarcini punctuale.
Instruire
Exercitiul 1
Două încărcături punctuale se află în mod arbitrar în interiorul unei suprafețe gaussiene S. Una dintre ele este cunoscută ca având o valoare de +3 nC (3 nano-coulomb). Dacă fluxul net de câmp electric prin suprafața Gaussiană este de 113 (N / C) mDouă, Care va fi valoarea celeilalte sarcini?
Soluţie
Legea lui Gauss prevede că
ΦȘI = (1 / εsau) ∙ Îenc
Prin urmare, taxa netă închisă este:
Îenc = ΦȘI ∙ εsau
Înlocuirea rezultatelor datelor:
Îenc = 113 (N / C) mDouă ∙ 8,85 x 10-12 (CDouă m-Două N-1) = 1 x 10-9 C = 1 nC.
Dar Îenc = + Q - q, unde sarcina pozitivă are o valoare cunoscută de +3 nC, prin urmare sarcina va fi în mod necesar -2 nC.
Exercițiul 2
În figura 2 există un aranjament (în stânga) a două sarcini pozitive, fiecare cu o valoare + q și un alt aranjament (în dreapta) cu o sarcină + q și cealaltă -q. Fiecare aranjament este închis într-o cutie imaginară cu toate marginile sale de 10 cm. Dacă | q | = 3 μC, găsiți fluxul net de câmp electric prin cutie pentru fiecare aranjament.
Soluţie
În primul aranjament fluxul net este:
ΦȘI = (1 / εsau) ∙ (+ q + q) = 678000 (N / C) mDouă
În aranjamentul din dreapta, fluxul net prin cutia imaginară care conține perechea de sarcini este zero..
Referințe
- Cosenza, M. Electromagnetism. Universitatea din Anzi.
- Díaz, R. Electrodinamică: note de clasă. Universitatea națională din Columbia.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 6. Electromagnetismul. Editat de Douglas Figueroa (USB).
- Jackson, J. D. Electrodinamică clasică. A treia. Ed. Wiley.
- Tarazona, C. Introducere în electrodinamică. Editorial Universitatea Manuela Beltrán.



Nimeni nu a comentat acest articol încă.