
Legea lui Grashof, mecanisme, exemple, aplicații
Legea lui Grashof afirmă că: Într-un mecanism plat cu patru bare articulate cu una dintre ele fixată, cel puțin una dintre bare poate face o întoarcere completă, cu condiția ca suma celei mai scurte bare și a celei mai lungi bare să fie mai mică sau egală cu suma celorlalte două.
Există cinci mecanisme plate cu patru bare sau legături care respectă legea lui Grashof (Un exemplu este prezentat în Figura 1). Pentru ca barele sau legăturile mecanismelor care respectă legea să facă o întoarcere completă, este necesar ca într-un aranjament real, fiecare bară să ocupe diferite planuri paralele.
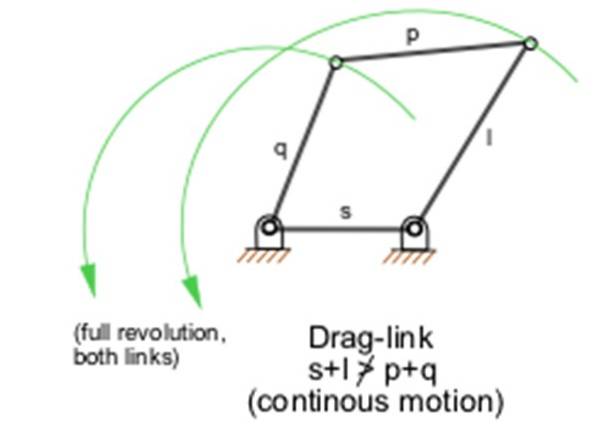
Legea lui Grashof este o regulă simplă care vă permite să proiectați un mecanism care necesită o rotație completă, fie pentru că un motor va fi conectat, fie, dimpotrivă, pentru că doriți să transformați o mișcare oscilatorie într-una rotativă, în așa fel încât să este matematic și viabil din punct de vedere fizic.
Indice articol
- 1 Cazuri limită
- 1.1 Tipuri de mișcare
- 2 Mecanisme care respectă legea lui Grashof
- 2.1 - Mecanism cu dublă manivelă
- 2.2 - Mai multe mecanisme care respectă legea lui Grashof
- 3 Aplicații
- 3.1 Mecanism de basculare
- 3.2 Mecanism paralelogram articulat
- 3.3 Mecanism anti-paralelogram articulat
- 4 Referințe
Cazuri limită
Să presupunem că cele patru bare de legătură au următoarele lungimi ordonate de la cel mai mic la cel mai mare în funcție de:
s> p> q> l
Legea lui Grashof prevede că pentru cel puțin o bară sau o legătură pentru a finaliza o revoluție sau un viraj, condiția trebuie îndeplinită:
s + l <= p + q
Această inegalitate are următoarele implicații:
- Singura bară sau legătură care poate da revoluții complete față de alta este cea mai scurtă bară.
- Dacă bara mai scurtă face ture complete față de alta, atunci va face și ture complete față de toate celelalte.
Tipuri de mișcare
Mișcarea patrulaterului articulat care respectă legea lui Grashof poate fi de următoarele tipuri:
- Întoarcere dublă sau manivelă, dacă cea mai scurtă bară este cea fixă și barele adiacente fac viraje complete.
- Înapoi și înapoi, dacă bara scurtă este adiacentă barei fixe.
- Rocker dublu, atâta timp cât cea mai scurtă bară este opusă celei fixe.
Când egalitatea este îndeplinită în formula Grashof, atunci suntem în cazul limitativ în care suma celei mai scurte bare cu cea mai lungă bară este egală cu suma celorlalte două.
În acest caz, mecanismul poate lua o configurație în care cele patru bare sunt aliniate. Și este în această poziție, îmbinările ne-fixe pot merge indiferent într-un sens sau altul, provocând blocarea mecanismului..
Mecanismele care îndeplinesc condiția Grashof sunt mai fiabile și suferă mai puțin stres asupra articulațiilor și legăturilor lor, în măsura în care sunt mai departe de cazul limitativ al egalității.
Mecanisme care respectă legea lui Grashof
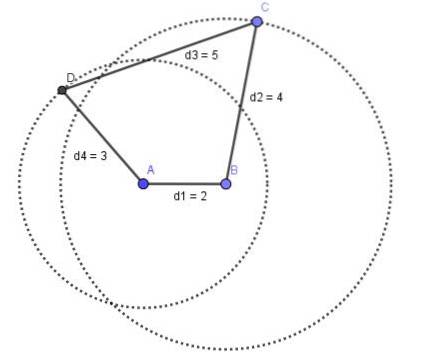
Vom indica îmbinările consecutive cu A, B, C și D, apoi:
- A și B sunt pivote fixe.
- AB = d1 (bară fixă)
- BC = d2
- CD = d3
- DA = d4
- Mecanism cu dublă manivelă
Barele b2 și b4 se rotesc complet și legea lui Grashof este îndeplinită:
d1 + d3 <= d2+d4.
- Mai multe mecanisme care respectă legea lui Grashof
Caracteristicile altor mecanisme care respectă legea lui Grashof sunt denumite și descrise mai jos:
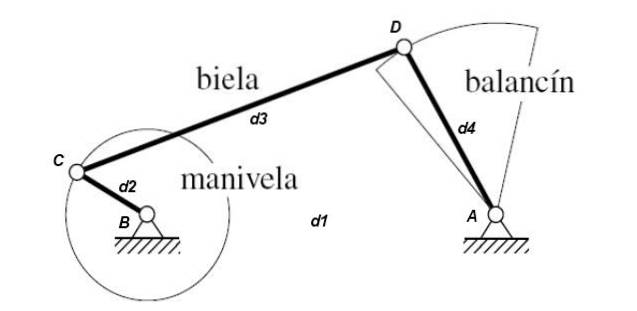
Mecanism cu manivelă - rocker
D2 + d3 este îndeplinit <= d1 + d4
Bara mai scurtă d2 se rotește complet, iar bara opusă d4 face o mișcare de basculare.
Mecanism dublu basculant
- Bara fixă AB este mai mare decât bara CD opusă și îndeplinește următoarele:
d1 + d3 <= d2 + d3
- Pentru bara mai scurtă (opusul barei fixe), este capabilă să facă un viraj complet.
Mecanism paralelogram articulat
- Barele AD și BC sunt de lungime egală și întotdeauna paralele.
- Pe de altă parte, barele AB și CD sunt de lungime egală și întotdeauna paralele.
- În cazul barelor opuse, acestea au aceeași lungime și d1 + d2 = d3 + d4 este îndeplinită, conform legii lui Grashof.
- În cele din urmă, barele AD și BC se întorc complet în aceeași direcție.
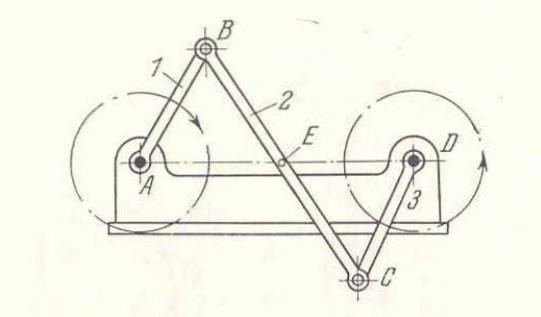
Anti-paralelogramă articulată
- Barele AD și BC sunt de lungime egală și nu paralele.
- Pentru barele AB și CD, acestea trebuie să fie de lungime egală și nu paralele.
- Pe de altă parte, barele opuse au aceeași lungime, două dintre ele sunt încrucișate.
- În acest mecanism, trebuie îndeplinită următoarea condiție:
d1 + d2 = d3 + d4
- Rotația barelor AD și BC este completă, dar în direcții opuse.
Aplicații
Mecanismele care respectă legea lui Grashof au mai multe aplicații:
Mecanism cu manivelă - Rocker
Se aplică mașinii de cusut cu pedale, utilă în locurile în care nu există electricitate, în care pedala face o mișcare de legănare sau balansare, care este transmisă unei roți conectate printr-un scripete la mașina de cusut.
Un alt exemplu de menționat este mecanismul ștergătorului de parbriz. În acest sens, un motor este conectat la manivela care efectuează viraje complete, transmițând o mișcare de basculare la bara care mută prima perie a sistemului..
O altă aplicație a mecanismului cu manivelă este cu brațele culbutor pentru pomparea uleiului de la sol.

Un motor este conectat la manivela care se rotește complet și transmite mișcarea capului de pompare sau brațului culbutor..
Mecanism paralelogram articulat
Acest mecanism era folosit pentru a conecta roțile locomotivelor cu abur, astfel încât ambele roți să se rotească în aceeași direcție și la aceeași viteză..
Principala caracteristică a acestui mecanism este că bara care leagă ambele roți are aceeași lungime ca separarea axelor lor..
Pantograful este un instrument de desen folosit pentru copierea și mărirea imaginilor. Se bazează pe un mecanism cu patru bare, în care există patru articulații care formează vârfurile unui paralelogram..
Mecanism anti-paralelogram articulat
Este mecanismul folosit în mașina de aruncat mingea de tenis, unde roțile care conduc și lansează mingea trebuie să se rotească în direcții opuse..
Referințe
- Clemente C. Laborator virtual al unui mecanism de basculare. Diplomă în inginerie mecanică. Universitatea din Almería. (2014). Recuperat de la: repositorio.ual.es
- Legea lui Hurtado F. Grashof. Recuperat de pe: youtube.com
- Mech Designer. Criteriul cinematic Grashof. Recuperat de la: mechdesigner.support.
- Shigley, J. Teoria mașinilor și mecanismelor. Mc-Graw Hill.
- Suntem F1. Analiza mecanismului cu patru bare. Recuperat de pe: youtube.com
- UNAM. Dezvoltarea unui mecanism cu patru bare pentru utilizare în predare. Recuperat de la: ptolomeo.unam.mx
- Wikipedia. Legătură cu patru bare. Recuperat de pe: en.wikipedia.com
- Wikipedia. Legea lui Grashof. Recuperat de pe: es.wikipedia.com



Nimeni nu a comentat acest articol încă.