impuls unghiular sau impuls unghiular este, pentru mișcarea de rotație, ceea ce este impulsul liniar pentru mișcarea de translație. Este o mărime vectorială care caracterizează rotația unei particule punctuale sau a unui obiect extins în jurul unei axe care trece printr-un punct.
Aceasta înseamnă că ori de câte ori trebuie calculat impulsul unghiular, axa de rotație trebuie specificată în mod corespunzător.
Începând cu un punct material de masă m, momentul unghiular este notat cu L, impuls liniar ca p iar poziția particulei față de o axă care trece printr-un anumit punct O este r, atunci:
L = r X p
Literele aldine sunt rezervate pentru cantități vectoriale, iar crucea înseamnă că impulsul unghiular este produsul vectorial între vectorul de poziție r iar momentul liniar p a particulei. Vectorul care rezultă dintr-un produs vector este perpendicular pe planul format de vectorii participanți.
Aceasta înseamnă că direcția și sensul L poate fi găsit folosind regula mâinii drepte pentru produsul încrucișat.
În sistemul internațional de unități SI, unitățile momentului unghiular sunt kg⋅mDouă/ s, care nu au un nume special. Și pentru un corp extins, care este compus din mai multe particule, definiția de mai sus este extinsă convenabil.
Indice articol
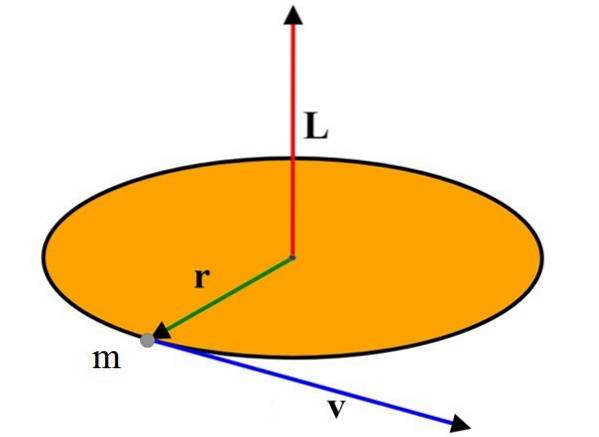
Mărimea vectorului momentului unghiular este în conformitate cu definiția produsului vector:
L = r⋅m⋅v⋅sen ϕ = mv (r⋅sen ϕ) = mvℓ
Unde ϕ este unghiul dintre vectori r Da v. Atunci ℓ = r sin ϕ este distanța perpendiculară între linia lui v și punctul O.
Pentru cazul particulei care se mișcă descriind circumferința prezentată în imaginea superioară, acest unghi este de 90 °, deoarece viteza este întotdeauna tangentă la circumferință și, prin urmare, perpendiculară pe rază..
Prin urmare, păcatul 90º = 1 și mărimea lui L este:
L = m⋅r⋅v
Momentul de inerție al unui corp rigid descrie inerția corpului împotriva rotației în jurul unei anumite axe.
Depinde nu numai de masa corpului, ci și de distanța față de axa de rotație. Acest lucru este ușor de înțeles atunci când credeți că pentru unele obiecte este mai ușor să se rotească în jurul unor axe decât altele..
Pentru un sistem de particule, momentul de inerție, notat cu litera I, este dat de:
I = ∑ reuDouă Δmeu
Unde Δmeu este o mică porție de aluat și reu este distanța sa față de axa de rotație. Un corp extins este compus din numeroase particule, de aceea momentul său total de inerție este suma tuturor produselor dintre masă și distanță, a particulelor care îl compun..
Dacă este un corp extins, însumarea se transformă într-o integrală și Δm devine un diferențial de masă dm. Limitele integrării depind de geometria obiectului:
I = ∫M (rDouă) dm
Conceptul de moment de inerție este strâns legat de impulsul unghiular al unui obiect extins, așa cum vom vedea mai jos.
Luați în considerare un sistem de particule, compus din mase Δmeu care se rotește după o circumferință în plan X y, fiecare are o viteză liniară legată de viteza sa unghiulară, cea din urmă fiind aceeași pentru toate particulele:
veu = ωreu
Unde reu este distanța față de axa de rotație O. Atunci magnitudinea impulsului unghiular este:
Leu = Δmeu. reu. (ωreu) = reuDouăω Δmeu
Momentul unghiular al sistemului va fi dat de suma:
L = ω ∑ reuDouă Δmeu
Identificăm rapid momentul de inerție, așa cum este definit în secțiunea anterioară, și, prin urmare, magnitudinea momentului său unghiular este următoarea:
L = Iω
După cum am spus că sistemul de particule se afla în planul xy, se dovedește că impulsul unghiular este direcționat de-a lungul axei z, perpendicular pe planul menționat. Direcția este dată de cea a rotației: impulsul unghiular este pozitiv dacă rotația se efectuează în sens invers acelor de ceasornic.
Un corp extins poate fi împărțit în felii, fiecare cu impuls unghiular dat de L = Iω îndreptate de-a lungul axei z. Dacă axa de simetrie a obiectului coincide cu axa z, nu există nicio problemă, deoarece chiar și pentru punctele care nu se află în planul xy, componentele momentului unghiular perpendicular pe acea axă se anulează.
Vectorial:
L = Euω
Această ecuație este valabilă pentru obiectele tridimensionale care se rotesc în jurul unei axe de simetrie.
Când o forță netă acționează asupra unei particule sau a unui corp, impulsul său se poate schimba și, în consecință, se va schimba și impulsul său unghiular. Pentru a ști când variază, folosim derivatul, care ne va oferi rata de schimbare în timp, dacă există una:
Aplicarea regulii produsului pentru derivat:
Termenul v x mv este nul, deoarece este produsul unui vector cu el însuși și, în al doilea termen, găsim forța netă F = mla, Prin urmare:
Produsul vector r X F nu este altceva decât cuplul sau cuplul net, uneori notat prin litera greacă τ sau ca M, întotdeauna cu caractere aldine, deoarece este o cantitate vectorială. Deci, în analogie cu impulsul liniar, impulsul unghiular variază atât timp cât există un cuplu net sau un cuplu:
dL/ dt = M
Din secțiunile precedente am văzut că:
dL/ dt = M
Adică, impulsul unghiular variază atunci când există un cuplu net. Dacă nu există cuplu net, atunci:
dL/ dt = 0 → L este constant
Cu alte cuvinte:
Momentul unghiular inițial = Momentul unghiular final
Acest rezultat este încă valabil chiar și în cazul în care un corp nu este rigid, așa cum vom vedea în exemplele următoare.
Momentul unghiular este o magnitudine importantă care se relevă în multe situații, ceea ce arată cât de universal este:
Ori de câte ori un corp rotativ se contractă, viteza sa de rotație crește, acest lucru este bine cunoscut patinatorilor de gheață..
Acest lucru se datorează faptului că, atunci când brațele și picioarele se contractă, momentul de inerție I scade, deoarece distanța dintre părțile lor scade, dar din moment ce impulsul unghiular este conservat, pentru a menține produsul Iω constant, viteza unghiulară trebuie să crească.
Acest lucru este valabil nu numai în patinaj, ci și în sporturi și activități în care este necesar să faci viraje, precum scafandri și trapeziști din circ..
Pisicile reușesc întotdeauna să aterizeze la patru picioare când cad. Deși nu au un impuls inițial, se asigură că își întorc rapid picioarele și coada pentru a-și schimba inerția de rotație și reușesc să aterizeze pe picioare..
La fel, în timp ce manevrează, impulsul lor unghiular este zero, deoarece rotația lor nu este continuă..
Un frisbee trebuie aruncat dându-i o rotire, astfel încât să zboare, altfel va cădea. Într-adevăr, impulsul unghiular oferit de lansator oferă pucului suficientă stabilitate pentru a se deplasa mai departe în aer..
Mingile din baseball, fotbal, baschet și alte sporturi au un impuls unghiular. Deoarece sunt sferice, au moment de inerție și sunt rotite în timpul jocului. Deoarece momentul de inerție al unei sfere este:
I = (2/5) MRDouă
Unde M este masa mingii și R raza acesteia, momentul de inerție în jurul unei anumite axe (fixe) este:
L = (2/5) MRDouăω
Luna se îndepărtează de Pământ, deoarece viteza de rotație a Pământului scade din cauza fricțiunii dintre masele mari de apă și fundul mării.
Sistemul Pământ-Lună își păstrează impulsul unghiular, prin urmare, dacă Pământul își scade contribuția, Luna își mărește contribuția, îndepărtându-se de Pământ..
Primul postulat al modelului atomic al lui Bohr afirmă că un electron ocupă doar orbite în care impulsul unghiular este un multiplu întreg al h / 2π, unde h este constanta lui Planck.
O tijă subțire de oțel are o masă de 500 g și o lungime de 30 cm. Se rotește în jurul unei axe care trece prin centrul său cu o rată de 300 de rotații pe minut. Determinați modulul impulsului său unghiular.
Vom avea nevoie de momentul de inerție al tijei referit la o axă care trece prin centrul ei. Consultând tabelele momentului de inerție se constată că:
I = (1/12) MLDouă = (1/12) × 0,5 kg x (30 × 10-Două m)Două = 3,75 × 10-3 kg.mDouă
Deoarece este un corp extins, din care știm viteza unghiulară, folosim:
L = Iω
Înainte de a transforma viteza unghiulară sau frecvența unghiulară ω la radiani / s:
ω = (300 rotații / minut) × (1 minut / 60 secunde) x (2π radiani / rotație) = 10 π rad / s
Înlocuind:
L = 3,75 x10-3 kg⋅mDouă × 10 π rad / s = 0,188 kg⋅mDouă / s
Nimeni nu a comentat acest articol încă.