Momentul formulelor de inerție, ecuațiilor și exemplelor de calcul

moment de inerție a unui corp rigid în raport cu o anumită axă de rotație, reprezintă rezistența sa la schimbarea vitezei sale unghiulare în jurul axei menționate. Este proporțional cu masa și, de asemenea, cu locația axei de rotație, deoarece corpul, în funcție de geometria sa, se poate roti mai ușor în jurul anumitor axe decât în ​​altele.

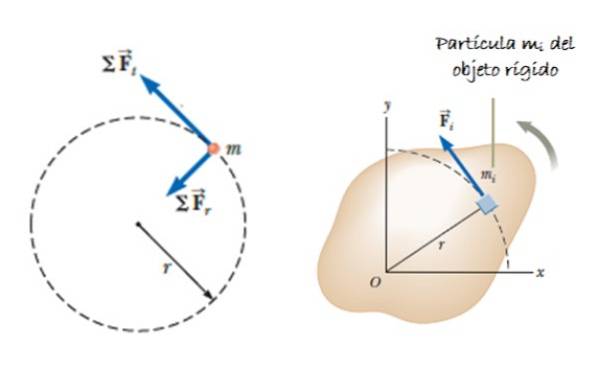
Să presupunem că un obiect mare (format din mai multe particule) care se poate roti în jurul unei axe. Să presupunem că o forță acționează F, aplicat tangențial pe elementul de masă Δm_eu, care produce un cuplu sau moment, dat de τ_net = ∑r_eu X F_eu. Vectorul r_eu este poziția lui Δm_eu (vezi figura 2).

Acest moment este perpendicular pe planul de rotație (direcție +k = ieșind din hârtie). Deoarece forța și vectorul de poziție radial sunt întotdeauna perpendiculare, produsul încrucișat rămâne:

τ_net = ∑ F_eu r_eu k = ∑ (Δm_eu la_eu) r_eu  k = ∑ Δm_eu (la_eu r_eu ) k

Accelerarea la_eu reprezintă componenta tangențială a accelerației, deoarece accelerația radială nu contribuie la cuplu. În funcție de accelerația unghiulară α, putem indica că:

la_eu = α r_eu

Prin urmare, cuplul net arată astfel:

τ_net = ∑ Δm_eu (α r_eu^Două) k = (∑ r_eu^Două Δm_eu) α k

Accelerația unghiulară α este aceeași pentru întregul obiect, prin urmare nu este afectată de indicele „i” și poate părăsi suma, care este tocmai momentul de inerție al obiectului simbolizat prin litera I:

I = ∑ r_eu^Două Δm_eu

Acesta este momentul de inerție al unei distribuții discrete de masă. Când distribuția este continuă, însumarea este înlocuită cu o integrală și Δm devine un diferențial de masă dm. Integrala se realizează asupra întregului obiect:

I = ∫_M(r^Două) dm

Unitățile momentului de inerție din sistemul internațional SI sunt kg x m^Două. Este o cantitate scalară și pozitivă, deoarece este produsul unei mase și al pătratului unei distanțe.

Indice articol

• 1 Exemple de calcul
  • 1.1 Momentul de inerție al unei bare subțiri față de o axă care trece prin centrul acesteia
  • 1.2 Momentul de inerție al unui disc față de o axă care trece prin centrul său
  • 1.3 Momentul de inerție al unei sfere solide în raport cu un diametru
  • 1.4 Momentul de inerție al unui cilindru solid față de axa axială
  • 1.5 Momentul de inerție al unei foi dreptunghiulare față de o axă care trece prin centrul acesteia
  • 1.6 Momentul de inerție al unei foi pătrate față de o axă care trece prin centrul acesteia
• 2 Teoremele momentului de inerție
  • 2.1 Teorema lui Steiner
  • 2.2 Teorema axelor perpendiculare
• 3 Exercițiul a fost rezolvat
• 4 Referințe

Exemple de calcul

Un obiect extins, cum ar fi o bară, un disc, o sferă sau altul, a cărui densitate ρ este constant și știind că densitatea este raportul masă - volum, diferențialul de masă dm este scris ca:

ρ = dm / dV → dm = ρdV

Înlocuind în integrală momentul de inerție, avem:

I = ∫r^Două ρdV = ρ ∫r^DouădV

Aceasta este o expresie generală, valabilă pentru un obiect tridimensional, al cărui volum V și poziția r sunt funcții ale coordonatelor spațiale X, Da Da z. Rețineți că, fiind constantă, densitatea se află în afara integralei.

Densitatea ρ Este, de asemenea, cunoscut sub numele de densitate volumetrică, dar dacă obiectul este foarte plat, ca o foaie sau foarte subțire și îngust ca o tijă, pot fi utilizate alte forme de densitate, să vedem:

- Pentru o foaie foarte subțire, densitatea de utilizat este σ, densitatea suprafeței (masa pe unitate de suprafață) și dă este diferențialul de zonă.

- Și dacă este o bară subțire, unde numai lungimea este relevantă, se folosește densitatea de masă liniară λ și un diferențial de lungime, în funcție de axa utilizată ca referință.

În exemplele următoare, toate obiectele sunt considerate a fi rigide (nedeformabile) și au densitate uniformă.

Momentul de inerție al unei bare subțiri față de o axă care trece prin centrul acesteia

Aici vom calcula momentul de inerție al unei bare subțiri, rigide, omogene, cu lungimea L și masa M, în raport cu o axă care trece prin mijloc.

În primul rând, este necesar să se stabilească un sistem de coordonate și să se construiască o figură cu geometria adecvată, astfel:

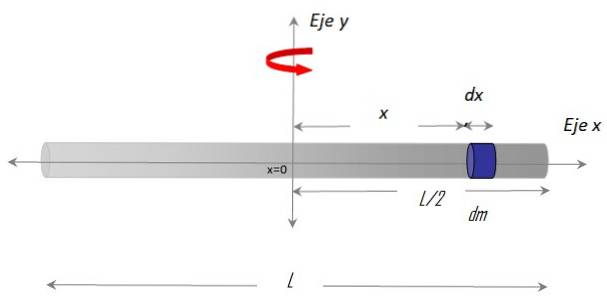
Axa X. de-a lungul barei și al Axa y ca axă de rotație. Procedura de stabilire a integralei necesită, de asemenea, alegerea unui diferențial de masă peste bară, numit dm, care are o lungime diferențială dx și se află în poziție X arbitrar, relativ la centru x = 0.

Conform definiției densității liniare de masă λ:

λ = M / L

Deoarece densitatea este uniformă, valabilă pentru M și L, este valabilă și pentru dm și dx:

λ = dm / dx → dm = λdx.

Pe de altă parte, elementul de masă este în poziție X, apoi prin substituirea acestei geometrii în definiție, avem o integrală definită, ale cărei limite sunt capetele barei conform sistemului de coordonate:

Înlocuind densitatea liniară λ = M / L:

Pentru a găsi momentul de inerție al barei față de o altă axă de rotație, de exemplu una care trece printr-una din extremele sale, puteți utiliza teorema lui Steiner (a se vedea exercițiul rezolvat la sfârșit) sau efectuați un calcul direct similar cu cel afișat aici, dar modificând geometria în mod corespunzător.

Momentul de inerție al unui disc față de o axă care trece prin centrul său

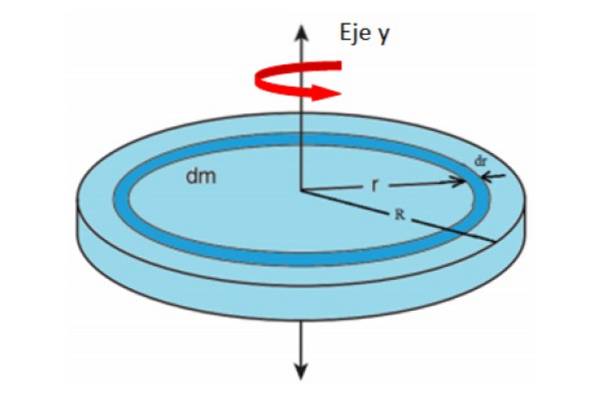
Un disc foarte subțire de grosime neglijabilă este o figură plană. Dacă masa este uniform distribuită pe întreaga suprafață a zonei A, densitatea masei σ este:

σ = M / Y

Atâta dm Ce dă corespund masei și zonei inelului diferențial prezentat în figură. Vom presupune că întregul ansamblu se rotește în jurul axei y.

Vă puteți imagina că discul este compus din multe inele concentrice de rază r, fiecare cu momentul respectiv de inerție. Adăugarea contribuțiilor tuturor inelelor până la atingerea razei R, momentul total de inerție al discului va fi.

σ = dm / dA → dm = σdă

Unde M reprezintă întreaga masă a discului. Aria unui disc depinde de raza sa r ca:

A = π.r^Două

Derivarea cu privire la r:

dA / dr = 2 = 2π.r → dA = 2π.rdr

Înlocuind cele de mai sus în definiția lui I:

Înlocuind σ = M / (π.R^Două ) rămâne:

Momentul de inerție al unei sfere solide în raport cu un diametru

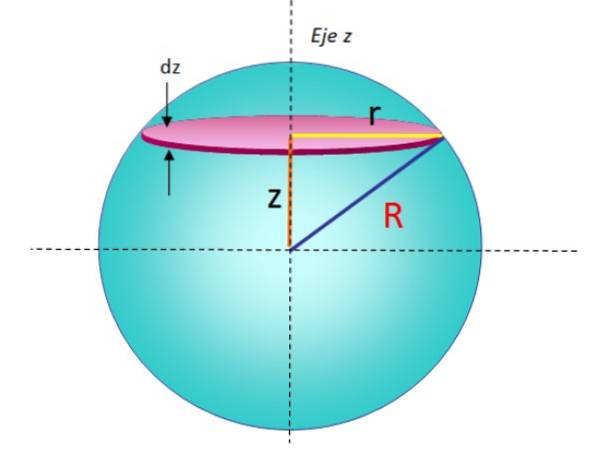
O sferă de rază R poate fi gândită ca o serie de discuri stivuite unul peste altul, unde fiecare disc de masă infinitesimală dm, radio r și grosimea dz, are un moment de inerție dat de:

a dat_disc = (½) r^Douădm

Pentru a găsi acest diferențial, am luat pur și simplu formula din secțiunea anterioară și am înlocuit-o M Da R pentru dm Da r, respectiv. Un disc ca acesta poate fi văzut în geometria figurii 5.

Prin adăugarea tuturor momentelor infinitezimale de inerție a discurilor stivuite, se obține momentul total de inerție al sferei:

Eu_sferă = ∫dI_disc

Ceea ce este echivalent cu:

I = ∫_sferă (½) r^Douădm

Pentru a rezolva integralul, trebuie să exprimați dm corect. Ca întotdeauna, se obține din densitate:

ρ = M / V = ​​dm / dV → dm = ρ.dV

Volumul unui disc diferențial este:

dV = Suprafața bazei x înălțimea

Înălțimea discului este grosimea dz, în timp ce aria bazei este πr^Două, Prin urmare:

dV = πr^Douădz

Și substituind integrala propusă ar arăta astfel:

I = ∫_sferă(½) r^Douădm = ∫ (½) r^Două(ρπr^Douădz)

Dar, înainte de integrare, trebuie observat că r -raza discului- depinde de z și R -raza sferei-, după cum se poate vedea din figura 5. Folosind teorema lui Pitagora:

R^Două = r^Două + z^Două → r^Două = R^Două - z^Două

 Ceea ce ne conduce la:

I = ∫_sferă(½) ρ r^Două(πr^Douădz) = ∫_sferă(½) ρ π r⁴dz= ∫_sferă(½) ρ π (R^Două - z^Două)^Două dz

Pentru a se integra pe întreaga sferă, observăm că z variază între -R și R, prin urmare:

Știind că ρ = M / V = ​​M / [(4/3) πR³] în cele din urmă se obține, după simplificare:

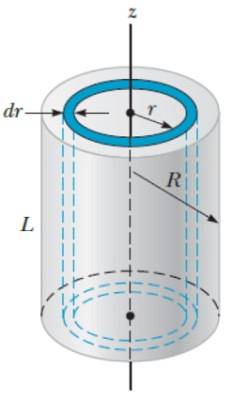
Momentul de inerție al unui cilindru solid față de axa axială

Pentru acest obiect se folosește o metodă similară cu cea utilizată pentru sferă, doar că de data aceasta este mai ușoară dacă se imaginează că cilindrul este format din cochilii cilindrice de rază r, grosime dr și înălțime H, de parcă ar fi straturile unei cepe.

Volumul dV a unui strat cilindric este:

dV = 2π.rL.dr

Prin urmare, masa cojii este:

dm = ρ.dV = ρ. 2π.r.L.dr

Această expresie este substituită în definiția momentului de inerție:

Ecuația de mai sus indică faptul că momentul de inerție al cilindrului nu depinde de lungimea acestuia, ci doar de masa și raza sa. da L schimbat, momentul de inerție față de axa axială va rămâne același. Din acest motiv, Eu cilindrului coincide cu cel al discului subțire calculat anterior.

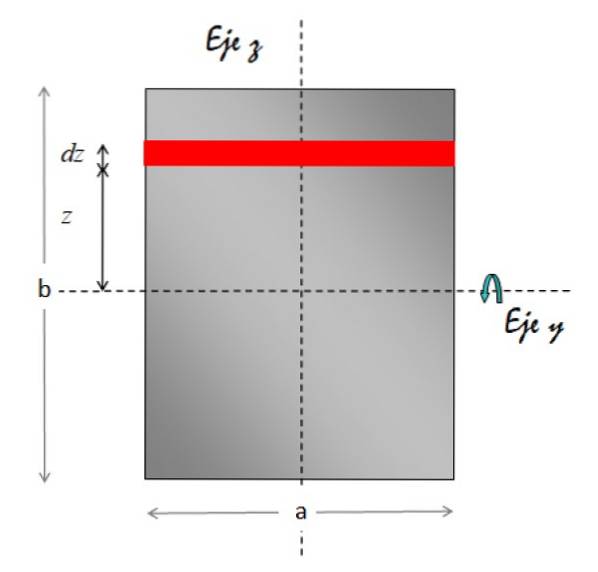
Momentul de inerție al unei foi dreptunghiulare față de o axă care trece prin centrul acesteia

Axa y axa orizontală de rotație. Figura de mai jos prezintă geometria necesară pentru realizarea integrării:

Elementul de zonă marcat cu roșu este dreptunghiular. Aria sa este baza x înălțimea, prin urmare:

dA = a.dz

Prin urmare, diferențialul de masă este:

dm = σ.dA = σ. (a.dz)

În ceea ce privește distanța de la elementul de zonă la axa de rotație, este întotdeauna z. Înlocuim toate acestea în integralitatea momentului de inerție:

Acum densitatea masei de suprafață σ este înlocuită cu:

σ = M / ab

Și cu siguranță arată astfel:

Rețineți că este ca cel cu bara subțire.

Momentul de inerție al unei foi pătrate față de o axă care trece prin centrul acesteia

Pentru un pătrat lateral L, în expresia anterioară valabilă pentru un dreptunghi, pur și simplu înlocuiți valoarea lui b pentru cea a L:

Teoremele momentului de inerție

Există două teoreme care sunt utile în special pentru simplificarea calculului momentelor de inerție cu privire la alte axe, care altfel ar putea fi dificil de găsit din cauza lipsei de simetrie. Aceste teoreme sunt:

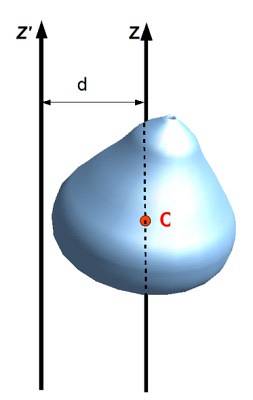
Teorema lui Steiner

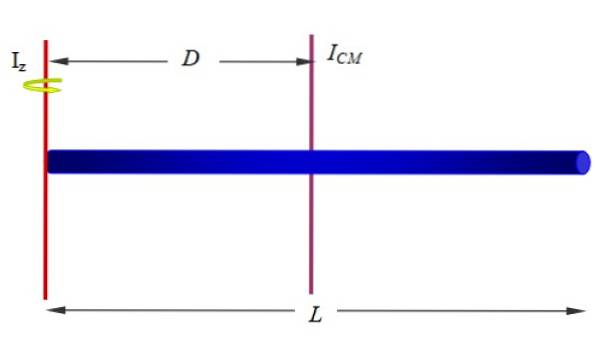
Numit si teorema axelor paralele, raportează momentul de inerție față de o axă cu alta care trece prin centrul de masă al obiectului, atâta timp cât axele sunt paralele. Pentru a-l aplica, este necesar să se cunoască distanța D dintre ambele axe și bineînțeles masa M a obiectului.

Fi Eu_z momentul de inerție al unui obiect extins cu privire la axa z, I_CM momentul inerției față de o axă care trece prin centrul de masă (CM) al obiectului menționat, atunci este adevărat că:

Eu_z = Eu_CM + MD^Două

Sau în notația următoarei figuri: Eu_{z '} = Eu_z + Md^Două

Teorema axelor perpendiculare

Această teoremă se aplică pe suprafețele plane și merge astfel: momentul de inerție al unui obiect plan în jurul unei axe perpendiculare pe acesta este suma momentelor de inerție din jurul a două axe perpendiculare pe prima axă:

Eu_z = Eu_X + Eu_Da

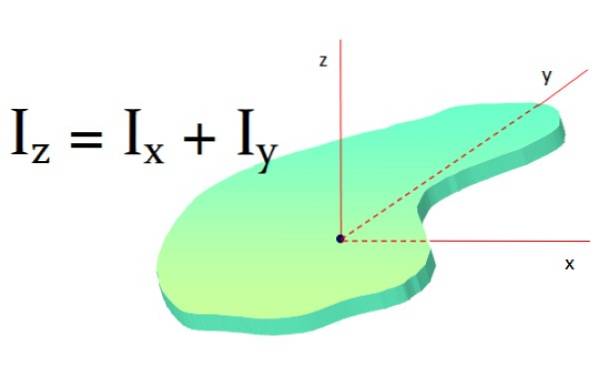
Dacă obiectul are simetrie astfel încât Eu_X și Eu_Da sunt egale, atunci este adevărat că:

Eu_z = 2I_X

Exercițiul a fost rezolvat

Găsiți momentul de inerție al barei în raport cu o axă care trece prin unul dintre capetele sale, așa cum se arată în figura 1 (mai jos și în dreapta) și figura 10.

Soluţie:

Avem deja momentul de inerție al barei în jurul unei axe care trece prin centrul său geometric. Deoarece bara este omogenă, centrul său de masă este în acel moment, deci acesta va fi al nostru Eu_CM pentru a aplica teorema lui Steiner.

Dacă lungimea barei este L, axa z este la o distanță D = L / 2, prin urmare:

Eu_z = Eu_CM + MD^Două= (1/12) ML^Două+M (L / 2)^Două= (1/3) ML^Două

Referințe

1. Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill. 313-340
2. Rex, A. 2011. Fundamentele fizicii. Pearson. 190-200.
3. Teorema axei paralele. Recuperat de la: hyperphysics.phy-astr.gsu.edu.
4. Serway, R. 2018. Fizica pentru știință și inginerie. Volumul 1. Cengage.
5. Universitatea din Sevilla. Momentul de inerție al solidelor sferice. Recuperat de pe: laplace.us.es.
6. Universitatea din Sevilla. Momentul de inerție al unui sistem de particule. Recuperat de pe: laplace.us.es.
7. Wikipedia. Teorema axei paralele. Recuperat de pe: en.wikipedia.org