Mișcarea pendulului

Care este mișcarea pendulului?

mișcarea pendulului Este o mișcare înainte și înapoi făcută de un obiect mai mult sau mai puțin greu, numit pendul, suspendat de o frânghie sau tijă ușoară, fixat la celălalt capăt al acestuia.

Pendulului i se dă un impuls inițial și i se permite să oscileze, în acest fel obiectul descrie arcuri înainte și înapoi. Acesta este principiul modului în care ceasurile pendulare, leagănele, scaunele balansoare și metronomi pendul, folosit pentru a marca vremurile în muzică.

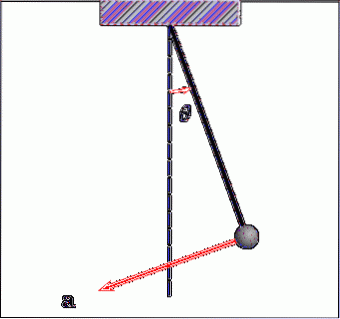
Se spune că în jurul anului 1581, Galileo Galilei a observat oscilația unei lămpi în catedrala din Pisa, observând că, deși amplitudinea oscilației candelabrului scădea din cauza fricțiunii cu aerul, nu a duratei ciclului lămpii..

Acest lucru a atras atenția lui Galileo, care a decis să continue studiul și a stabilit că perioada pendulului nu depinde de masă, ci de rădăcina pătrată a lungimii coardei, așa cum se va vedea mai târziu..

Caracteristicile mișcării pendulului

Un pendul este foarte ușor de construit, deoarece este suficient cu o linie plumbă atârnată de un fir de bumbac și ținută de celălalt capăt cu degetele sau prin atașarea acestuia la un suport ca un cui..

După micul impuls inițial, greutatea este însărcinată cu menținerea pendulului oscilant, deși frecarea scade amplitudinea mișcării, până când încetează complet..

Principala caracteristică a mișcării pendulului este să fie repetitivă, deoarece este o mișcare înainte și înapoi. Acum, pentru a facilita studiul său, este convenabil să faceți unele simplificări pentru a vă concentra pe un model mai simplu, numit pendul simplu.

Pendulul simplu

Este un sistem ideal care constă dintr-o linie plumbă, considerată ca o masă punctuală m, atașat la o frânghie ușoară, inextensibilă, de lungime L. Caracteristicile acestui sistem sunt:

• Au o mișcare repetitivă și periodică, constând în mersul înainte și înapoi al unui arc de circumferință de rază egal cu L.
• Nu ia în considerare frecarea.
• Gama de mișcare este mică (< 5º).
• Perioada este independentă de masă m, și depinde numai de lungime L pendul.

Formule și ecuații

Următoarea este o diagramă a pendulului simplu, pe care acționează două forțe: greutatea P de magnitudine mg, care este direcționată vertical în jos și tensiunea T Pe frânghie. Fricțiunea nu este luată în considerare.

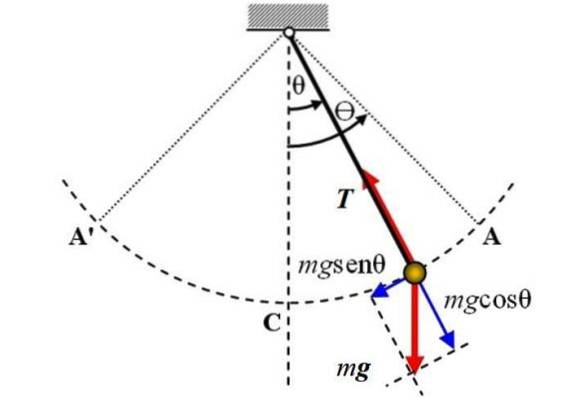
Axa de referință este axa verticală și coincide cu poziția θ = 0, de acolo se măsoară deplasarea unghiulară either, fie într-o direcție, fie în alta. Semnul + poate fi atribuit schimbării la dreapta din figură.

Pentru a studia mișcarea pendulului, se alege un sistem de coordonate cu originea de la pendul în sine. Acest sistem are o coordonată tangențială față de arcul de circumferință A'CA descris de pendul, precum și o coordonată radială, îndreptată spre centrul traiectoriei..

În momentul prezentat în figură, pendulul se deplasează spre dreapta, dar componenta tangențială a gravitației, numită F_t, este responsabil pentru a-l face să se întoarcă. Din figură se poate observa că această componentă are direcția opusă mișcării.

În ceea ce privește tensiunea din coardă, aceasta este echilibrată cu componenta greutății mgcosθ.

Deplasarea unghiulară 

Trebuie să exprimăm ecuația în termenii unei singure variabile, amintindu-ne că deplasarea unghiulară θ și arcul parcurs sunt legate de ecuație:

s = L.θ

Masa se anulează pe ambele părți și dacă amplitudinea este mică, unghiul θ, de asemenea, este valabilă următoarea aproximare:

sen θ ≈ θ

Cu aceasta, se obține următoarea ecuație diferențială pentru variabila θ (t):

Această ecuație este foarte ușor de rezolvat, deoarece soluția sa este o funcție a cărei a doua derivată este funcția în sine. Există trei alternative: un cosinus, un sinus sau un exponențial. Funcția cosinusului este aleasă pentru deplasarea unghiulară θ (t), deoarece este o funcție bine cunoscută și ușor de manevrat.

Cititorul poate verifica, prin diferențierea de două ori, că următoarea funcție îndeplinește ecuația diferențială:

θ (t) = θ_m cos (ωt + φ)

Unde θ_m este unghiul maxim pe care pendulul îl mișcă față de verticală și frecvența unghiulară ω este:

Ecuația perioadei

Perioada T a mișcării este timpul necesar pentru a executa un ciclu și este definită ca:

Înlocuind ω:

După cum sa menționat mai sus, perioada nu depinde de masa pendulului, ci doar de lungimea acestuia..

Exemple de mișcare a pendulului

Măsurarea ritmului cardiac

Galileo a avut ideea de a măsura ritmul cardiac al oamenilor, de a regla lungimea pendulului pentru a face ca perioada să coincidă cu bătăile inimii unei persoane..

Ceasul cu pendul

Acesta este, fără îndoială, unul dintre cele mai familiare exemple de mișcare a pendulului. Realizarea ceasului cu pendul este atât despre știință cât și despre artă. Fizicianul olandez Christian Huygens (1629-1695) a dezvoltat primul ceas cu pendul în 1656, pe baza studiului făcut cu ani în urmă de Galileo.

Pendulul lui Foucault

Este un pendul oarecum diferit de cel descris mai sus, deoarece este capabil să se rotească în orice plan vertical. A fost creat de fizicianul francez Léon Foucault (1819-1868) și este folosit pentru a vizualiza rotația Pământului.

Exercițiul a fost rezolvat

Un pendul simplu trece la fiecare 0,5 s prin poziția de echilibru. Care este lungimea firului?

Soluţie

Deoarece perioada este timpul necesar pentru a finaliza un ciclu complet, în care trece de două ori prin poziția de echilibru: unul merge și altul înapoi, atunci:

T = 2 × 0,5 s = 1 s

Din:

Lungimea L a firului este degajată:

Firul are o lungime de 0,25m sau 25cm.

Referințe

1. Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 2. Dinamica. Editat de Douglas Figueroa (USB).
2. Giambattista, A. 2010. Fizică. Al 2-lea. Ed. McGraw Hill.
3. Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
4. Katz, D. 2013. Fizica pentru oamenii de știință și ingineri. Fundamente și conexiuni. Cengage Learning.
5. Knight, R. 2017. Fizica pentru oamenii de știință și inginerie: o abordare strategică. Pearson.