
Metoda Euler pentru ce este, procedură și exerciții
Metoda lui Euler este cea mai simplă și simplă dintre procedurile utilizate pentru a găsi soluții numerice aproximative la o ecuație diferențială obișnuită de ordinul întâi, cu condiția să fie cunoscută starea sa inițială.
O ecuație diferențială obișnuită (ODE) este ecuația care leagă o funcție necunoscută a unei singure variabile independente cu derivatele sale.
Dacă cea mai mare derivată care apare în ecuație este de gradul unu, atunci este o ecuație diferențială obișnuită de gradul I.
Cel mai general mod de a scrie o ecuație de gradul I este:

x = x0
y = y0
Indice articol
- 1 Care este metoda lui Euler?
- 2 exerciții rezolvate
- 2.1 Exercițiul 1
- 2.2 Exercițiul 2
- 2.3 Exercițiul 3
- 3 Dinamica lui Newton și metoda lui Euler
- 3.1 Exercițiul 4
- 4 Exerciții propuse pentru acasă
- 4.1 Exercițiul 1
- 4.2 Exercițiul 2
- 5 Referințe
Care este metoda lui Euler?
Ideea metodei lui Euler este de a găsi o soluție numerică la ecuația diferențială în intervalul dintre X0 și XF .
În primul rând, intervalul este discretizat în n + 1 puncte:
X0, X1, XDouă, X3..., Xn
Care se obțin astfel:
Xeu= x0+ih
Unde h este lățimea sau pasul subintervalelor:

Cu condiția inițială, atunci este, de asemenea, posibil să se cunoască derivata la început:
y '(xsau) = f (xsau, Dasau)
Această derivată reprezintă panta liniei tangente la curba funcției y (x) tocmai la punctul:
Ao = (xsau, Dasau)
Apoi, o predicție aproximativă a valorii funcției y (x) se face la următorul punct:
y (x1) ≈ și1
Da1 = Dasau +(X1- Xsau) f (xsau, Dasau) = șisau + h f (xsau, Dasau)
S-a obținut apoi următorul punct aproximativ al soluției, care ar corespunde:
LA1 = (x1, Da1)
Procedura se repetă pentru a obține punctele succesive
LADouă, LA3..., Xn
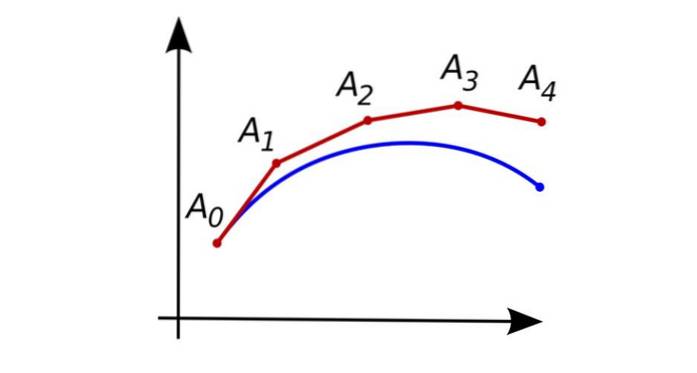
În figura prezentată la început, curba albastră reprezintă soluția exactă a ecuației diferențiale, iar cea roșie reprezintă punctele aproximative succesive obținute prin procedura Euler.
Exerciții rezolvate
Exercitiul 1
Eu) Fie ecuația diferențială:

Cu condiția inițială x = a = 0; Dala= 1
Folosind metoda lui Euler, obțineți o soluție aproximativă de Da în coordonata X = b = 0,5, împărțind intervalul [a, b] în n = 5 părți.
Soluţie

Rezultatele numerice sunt rezumate după cum urmează:

De unde se concluzionează că soluția Y pentru valoarea 0,5 este 1,4851.
Notă: pentru a efectua calculele, Studioul Smath, program de utilizare gratuită.
Exercițiul 2
II) Continuând cu ecuația diferențială din exercițiul I), găsiți soluția exactă și comparați-o cu rezultatul obținut prin metoda lui Euler. Găsiți eroarea sau diferența dintre rezultatul exact și aproximativ.
Soluţie

Soluția exactă nu este foarte dificil de găsit. Derivata funcției sin (x) este cunoscută a fi funcția cos (x). Prin urmare, soluția y (x) va fi:
y (x) = sin x + C
Pentru ca condiția inițială să fie îndeplinită și (0) = 1, constanta C trebuie să fie egală cu 1. Rezultatul exact este apoi comparat cu cel aproximativ:
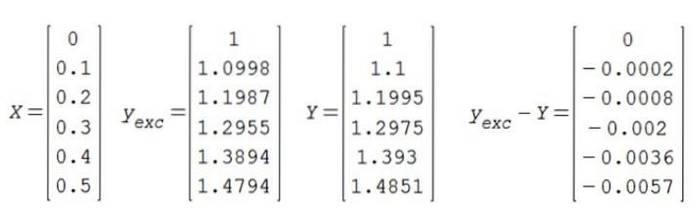
Se concluzionează că, în intervalul calculat, aproximarea are trei cifre semnificative de precizie.
Exercițiul 3
III) Luați în considerare ecuația diferențială și condițiile sale inițiale date mai jos:
y '(x) = - yDouă
Cu condiția inițială x0 = 0; Da0 = 1
Utilizați metoda Euler pentru a găsi valori aproximative ale soluției y (x) în interval x = [0, 1,5]. Folosiți pasul h = 0,1.
Soluţie
Metoda lui Euler este foarte potrivită pentru a fi utilizată cu o foaie de calcul. În acest caz vom folosi foaia de calcul a geogebra, un program gratuit și gratuit de utilizat.
Foaia de calcul din figură arată trei coloane (A, B, C) prima este variabila X , a doua coloană reprezintă variabila Da, iar a treia coloană derivată Y '.
Rândul 2 conține valorile inițiale ale X, Da, Y ' .
Pasul valoric 0.1 a fost plasat în celula poziției absolute ($ D $ 4).
Valoarea inițială a lui y0 se află în celula B2, iar y1 se află în celula B3. Pentru a calcula y1 se folosește formula:
Da1 = Dasau +(X1- Xsau) f (xsau, Dasau) = șisau + h f (xsau, Dasau)
Această formulă de calcul tabelar ar fi Numărul B3: = B2 + $ D $ 4 * C3.
În mod similar, y2 ar fi în celula B4, iar formula sa este prezentată în figura următoare:
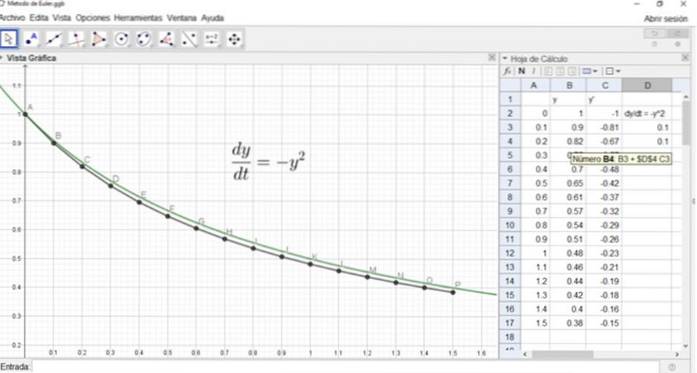
Figura arată, de asemenea, graficul soluției exacte și punctele A, B,…, P ale soluției aproximative prin metoda lui Euler.
Dinamica newtoniană și metoda lui Euler
Dinamica clasică a fost dezvoltată de Isaac Newton (1643 - 1727). Motivația inițială a lui Leonard Euler (1707 - 1783) de a-și dezvolta metoda, a fost tocmai rezolvarea ecuației celei de-a doua legi a lui Newton în diferite situații fizice..
A doua lege a lui Newton este de obicei exprimată ca o ecuație diferențială de gradul al doilea:

Unde X reprezintă poziția unui obiect în momentul respectiv t. Acest obiect are o masă m și este supus unei forțe F. Functia F este legat de forță și masă după cum urmează:


Pentru a aplica metoda Euler sunt necesare valorile inițiale ale timpului t, viteză v și poziția X.
Tabelul următor explică modul în care pornind de la valorile inițiale t1, v1, x1 se poate obține o aproximare a vitezei v2 și a poziției x2, în momentul t2 = t1 + Δt, unde Δt reprezintă o mică creștere și corespunde pasului în metoda lui Euler.

Exercițiul 4
IV) Una dintre problemele fundamentale în mecanică este aceea a unui bloc de masă M legat de un arc (sau arc) de constantă elastică K.
A doua lege a lui Newton pentru această problemă ar arăta astfel:
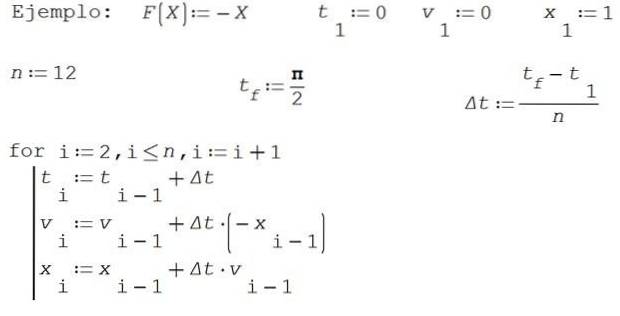
În acest exemplu, pentru simplitate, vom lua M = 1 și K = 1. Găsiți soluții aproximative pentru poziție X și viteză v prin metoda lui Euler pe intervalul de timp [0, π / 2] împărțind intervalul în 12 părți.
Luați 0 ca instant inițial, viteza inițială 0 și poziția inițială 1.
Soluţie
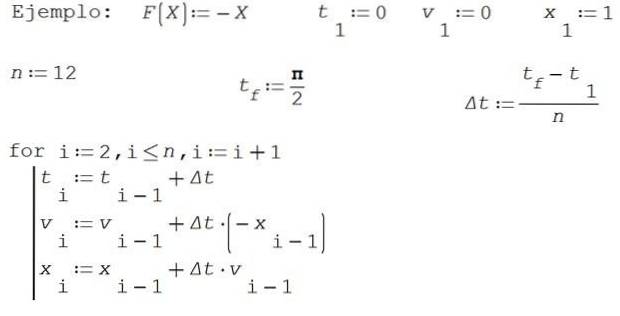
Rezultatele numerice sunt prezentate în tabelul următor:
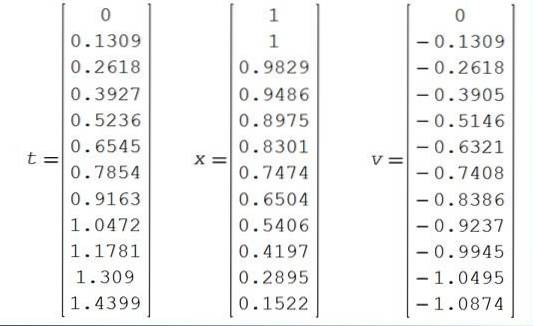
Sunt prezentate și graficele poziției și vitezei între instantele 0 și 1,44..
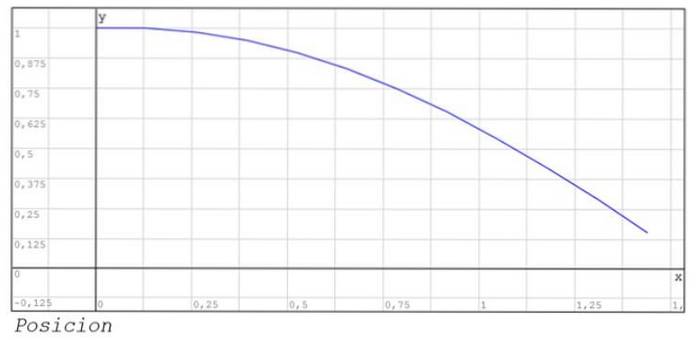
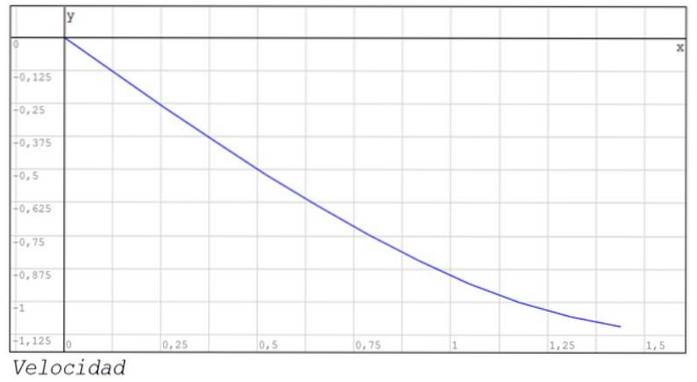
Exerciții propuse pentru acasă
Exercitiul 1
Utilizați o foaie de calcul pentru a determina o soluție aproximativă folosind metoda Euler pentru ecuația diferențială:
y '= - Exp (-y) cu condițiile inițiale x = 0, y = -1 în intervalul x = [0, 1]
Începeți cu un pas de 0,1. Complotați rezultatul.
Exercițiul 2
Folosind o foaie de calcul găsiți soluții numerice la următoarea ecuație pătratică, unde y este o funcție a variabilei independente t.
y "= - 1 / y² cu condiția inițială t = 0; y (0) = 0,5; y '(0) = 0
Găsiți soluția pe intervalul [0,5; 1.0] folosind un pas de 0,05.
Trageți rezultatul: y vs t; tu 'vs t
Referințe
- Metoda lui Eurler Luată de pe wikipedia.org
- Euler rezolvator. Luată de pe en.smath.com


Nimeni nu a comentat acest articol încă.