
Notare dezvoltată ce este, exemple și exerciții
notație extinsă este una în care o cifră numerică este exprimată ca o sumă în care se ia în considerare valoarea pozițională a fiecărei cifre care alcătuiește numărul.
De exemplu, atunci când scrieți o cifră ca 2345, fiecare cifră din ea are o ierarhie pozițională. Citind de la cifra extremă dreaptă la stânga, ierarhia sau valoarea crește.
În numărul 2345, cifra 5 reprezintă cinci unități, cifra 4 reprezintă patru zeci, 3 corespunde poziției a treia de la stânga la dreapta și, prin urmare, 3 reprezintă trei sute, în cele din urmă 2 reprezintă două mii. Cu alte cuvinte, în notație dezvoltată sau extinsă, figura 2345 este scrisă astfel:
2345 = 2 mii + 3 sute + 4 zeci + 5 cele
Dar poate fi exprimat și după cum urmează:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
De asemenea, figura 2345 poate fi scrisă ca suma puterilor a 10:
2345 = 2 x 10 ^ 3 + 3 x 10 ^ 2 + 4 x 10 ^ 1 + 5 x 10 ^ 0
Unde circumflexul ^ înseamnă ridicarea la exponentul indicat. De exemplu, 10 ^ 3 = 10 x 10 x 10 = 1000. O altă modalitate de a scrie exponenții este folosind un supercript:
2345 = 2 x 103 + 3 x 10Două + 4 x 101 + 5x100
Indice articol
- 1 Sistem de numerotare pozițională
- 1.1 Numere fracționate sau zecimale
- 2 Exemple de notație extinsă
- 2.1 Exemplul 1
- 2.2 Exemplul 2
- 3 Exerciții de notație extinsă
- 3.1 Exercițiul 1
- 3.2 Exercițiul 2
- 3.3 Exercițiul 3
- 3.4 Exercițiul 6
- 4 Referințe
Sistem de numerotare pozițională
Sistemul cu cifre arabe sunt numerele care sunt utilizate zilnic în marea majoritate a continentelor și țărilor lumii. Cifrele arabe sunt un sistem de bază 10, deoarece zece simboluri sau grafeme sunt folosite pentru a scrie orice număr. Aceste zece simboluri sunt:
0 1 2 3 4 5 6 7 8 9
Cu doar unul dintre aceste simboluri, cifrele de la zero la nouă pot fi exprimate. Pentru a exprima cifre mai mari de nouă, se utilizează sistemul pozițional din baza zece. Numărul 10 este unități de zece și zero. Numărul 11 este un zece și o unitate. Numărul 123 (o sută douăzeci și trei) este o sută, două zeci și trei. Scris sub formă de puteri de zece, numărul 123 va fi:
1 × 10 ^ 2 + 2 × 10 ^ 1 + 3 × 10 ^ 0
Unde:
10 ^ 2 = 10 x 10 = 100
10 ^ 1 = 10
10 ^ 0 = 1.
Cu acest exemplu este clar că poziția cifrei la extrema dreaptă este poziția 0 și reprezintă numărul de unități, cea a celei de-a doua cifre de la dreapta la stânga este poziția 1 și reprezintă numărul de zeci, a treia cifră (de la dreapta stânga) are poziția 2 și reprezintă sutele.
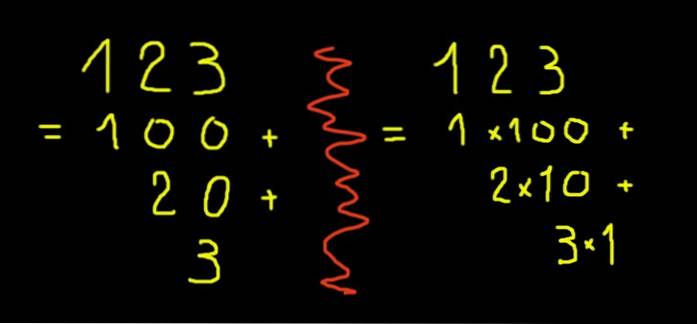
Numere fracționate sau zecimale
Cu sistemul de poziție zecimal, este, de asemenea, posibil să se reprezinte numere sau cifre care sunt mai mici decât unitatea sau care sunt mai mari decât unitatea, dar nu întregi, adică au fracții ale unității.
Pentru a reprezenta în sistemul zecimal arab fracția ½, adică jumătate din unitate, este scrisă:
½ = 0,5
Pentru a ajunge la această expresie în sistemul nostru de bază 10, s-au efectuat implicit următoarele operații:
1- Numărătorul și numitorul sunt înmulțiți cu 5 pentru a avea fracția echivalentă 5/10 = 1/2.
2- Împărțirea cu 10 este echivalentă cu înmulțirea cu puterea din baza zece cu exponent minus unu (10 ^ -1), adică 5/10 = 5 × 10 ^ -1.
3- Exponentul negativ indică de câte ori cifra indicată este mutată sau poziționată spre dreapta din poziția unității, în cazul nostru ar fi 0,5.
4- ½ = 0,5 în notație extinsă se scrie astfel:
0,5 = 0x10 ^ 0 + 5 × 10 ^ -1
Unde 10 ^ -1 = 0,1 este o zecime (fracțiunea corespunzătoare unității împărțită în 10 părți egale).
În acest fel, numărul 0,5 corespunde cu cinci zecimi, dar numărul 0,05 corespunde cu 5 sutimi și 0,005 până la 5 miimi.
Exemple de notație extinsă
Exemplul 1
Având în vedere cifra 40201 în notație standard, convertiți-o în notație extinsă.
Soluţie:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Exemplul 2
Scrieți fracția ¾ în notație extinsă.
Soluţie:
În acest caz, aveți trei sferturi din unitate.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10 ^ -1 + 5 × 10 ^ -2.
Spus în cuvinte ar arăta astfel:
Fracția ¾ corespunde la șapte zecimi plus cinci sutimi.
Exerciții de notație extinsă
Exercitiul 1
Spuneți în cuvinte expresia extinsă a figurii 40201 din exemplul 1.
Soluţie:
Notația dezvoltată arată astfel:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
Că în limbajul cuvintelor se spune:
Patru zeci de mii, plus zero mii, plus două sute, plus zero zeci, plus o unitate.
Exercițiul 2
Exprimați figura anterioară în cuvinte și descompuneți expresia corespunzătoare în formă extinsă.
Soluţie:
Cifra 40201 în cuvinte este exprimată astfel:
Patruzeci de mii două sute unu
Propoziția anterioară poate fi dezvoltată ca:
40 × 1000 + 2 × 100 + 1
Se poate spune că modul de pronunțare a figurilor este un mod semi-dezvoltat de a le exprima.
Exercițiul 3
Scrieți în formă extinsă numărul 7/3.
Soluţie:
Este o cifră exprimată ca o fracțiune necorespunzătoare, întrucât numeratorul este mai mare decât numitorul, cifra este mai mare decât unitatea.
Această fracțiune necorespunzătoare poate fi descompusă ca suma fracțiilor 6/3 + 1/3. Prima dintre fracții are ca rezultat un număr întreg 2, în timp ce 1/3 = 0,333333, unde cifra 3 se repetă la nesfârșit. Deci, expresia zecimală extinsă a figurii 7/3 va fi întotdeauna o expresie aproximativă:
7/3 = 2 + 1/3 ≃ 2 + 0.333 = 2 + 3 × 10 ^ -1 + 3 × 10 ^ -2 + 3 × 10 ^ -3.
Exercițiul 6
Scrieți în notație standard și apoi în formă extinsă numărul: Douăzeci și trei de miliarde două sute cincizeci de milioane cinci sute douăzeci și șase de mii trei sute douăzeci și cinci și trei douăzeci și trei de miimi.
Soluţie:
Trebuie amintit că a miliard este echivalentul unui miliard. Cuvantul miliard a fost acceptată de Academia Regală Spaniolă în 1995 la cererea regretatului președinte venezuelean Rafael Caldera, membru al Academiei Venezuelene de Limbă. În acest caz, figura pentru exercițiul în notație standard este scrisă astfel:
23.2501526.325.023
23 miliarde + 250 milioane + 526 mii + 325 unități + 23 miimi.
23 × 10 ^ 9 + 250 × 10 ^ 6 + 526 × 10 ^ 3 + 325 × 10 ^ 0 + 23 × 10 ^ -3
În cele din urmă, figura este scrisă în notație extinsă:
2 × 10 ^ 10 + 3 × 10 ^ 9 + 2 × 10 ^ 8 + 5 × 10 ^ 7 + 0x10 ^ 6 + 5 × 10 ^ 5 + 2 × 10 ^ 4 + 6 × 10 ^ 3 + 3 × 10 ^ 2 + 2 × 10 ^ 1 + 5 × 10 ^ 0 + 0x10 ^ -1 + 2 × 10 ^ -2 + 3 × 10 ^ -3.
Referințe
- Academia Khan. Diagramele valorii plasate. Recuperat de pe: es.khanacademy.org
- Academia Khan. Scrieți un număr în formă extinsă (video). Recuperat de pe: es.khanacademy.org
- Ifrah, Geoges (1998): Istoria universală a figurilor. Espasa Calpe S.A.
- Wikipedia. Notatie pozitionala. Recuperat de pe: es.wikipedia.com
- Wikipedia. Miliard. Recuperat de pe: es.wikipedia.com



Nimeni nu a comentat acest articol încă.