
Caracteristicile undei sinusoidale, părți, calcul, exemple
unde sinusoidale Sunt modele de unde care pot fi descrise matematic prin funcțiile sinus și cosinus. Ele descriu cu exactitate evenimentele naturale și semnalele care variază în timp, cum ar fi tensiunile generate de centralele electrice și apoi utilizate în case, industrii și străzi.
Elementele electrice, cum ar fi rezistențele, condensatoarele și inductanțele, care sunt conectate la intrările de tensiune sinusoidală, produc și răspunsuri sinusoidale. Matematica utilizată în descrierea sa este relativ simplă și a fost studiată cu atenție..

Matematica undelor sinusoidale sau sinusoidale, așa cum sunt și ele cunoscute, este cea a funcțiilor sinus și cosinus.
Acestea sunt funcții repetitive, ceea ce înseamnă periodicitate. Ambele au aceeași formă, cu excepția faptului că cosinusul este deplasat spre stânga față de sinus cu un sfert de ciclu. Se poate vedea în figura 2:

Atunci cos x = sin (x + π / 2). Cu ajutorul acestor funcții este reprezentată o undă sinusoidală. Pentru a face acest lucru, magnitudinea în cauză este plasată pe axa verticală, în timp ce timpul este situat pe axa orizontală..
Graficul de mai sus arată, de asemenea, calitatea repetitivă a acestor funcții: modelul se repetă continuu și regulat. Datorită acestor funcții, este posibil să se exprime tensiuni și curenți sinusoidali care variază în timp, plasându-i pe axa verticală în loc de Da, A v sau unul eu pentru a reprezenta tensiunea sau curentul, și pe axa orizontală în loc de X, t vreme.
Cel mai general mod de a exprima o undă sinusoidală este:
v (t) = vm sen (ωt + φ)
Apoi vom aprofunda sensul acestei expresii, definind câțiva termeni de bază pentru a caracteriza unda sinusoidală.
Indice articol
- 1 Piese
- 1.1 Perioada
- 1.2 Amplitudine
- 1.3 Ciclul
- 1.4 Frecvența
- 1.5 Faza
- 2 Generator de unde sinusoidale
- 2.1 Aplicarea legii Faraday
- 2.2 Oscilator Wien
- 3 Cum se calculează undele sinusoidale?
- 3.1 Osciloscopul
- 4 Exemple
- 4.1 Exemplul 1
- 4.2 Exemplul 2
- 5 Referințe
Părți
Perioada, amplitudinea, frecvența, ciclul și faza sunt concepte aplicate undelor periodice sau repetitive și sunt importante pentru a le caracteriza corect..
Perioadă
O funcție periodică precum cele menționate, care se repetă la intervale regulate, îndeplinește întotdeauna următoarea proprietate:
f (t) = f (t + T) = f (t + 2T) = f (t + 3T) = ... .
Unde T este o cantitate numită perioada de val, y este timpul necesar pentru a repeta o fază a aceluiași. În unitățile sistemului internațional, perioada este măsurată în secunde.
Amplitudine
Conform expresiei generale a undei sinusoidale v (t) = vm păcat (ωt + φ), vm este valoarea maximă a funcției, care apare atunci când sin (ωt + φ) = 1 (amintind că cea mai mare valoare pe care o admit atât funcțiile sinusoidale, cât și cele ale cosinusului este 1). Această valoare maximă este exact amplitudinea undei, de asemenea cunoscut ca si amplitudinea de vârf.
În cazul unei tensiuni va fi măsurată în Volți și dacă este un curent va fi în Amperi. În unda sinusoidală prezentată amplitudinea este constantă, dar în alte tipuri de undă amplitudinea poate varia.
Ciclu
Este o parte a valului conținut într-o perioadă. În figura anterioară, perioada a fost luată măsurând-o de la două vârfuri consecutive sau creste, dar poate începe să fie măsurată din alte puncte ale valului, atât timp cât acestea sunt limitate de o perioadă.
Observați în figura următoare cum un ciclu acoperă de la un punct la altul cu aceeași valoare (înălțime) și aceeași pantă (înclinare).
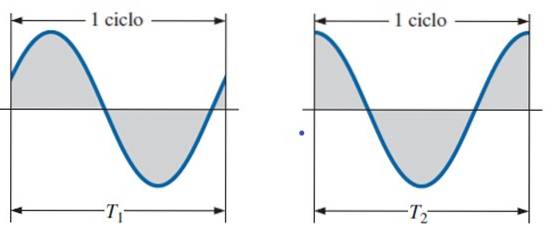
Frecvență
Este numărul de cicluri care apar în 1 secundă și este legat de argumentul funcției sinusoidale: ωt. Frecvența este notată ca F și se măsoară în cicluri pe secundă sau Hertz (Hz) în sistemul internațional.
Frecvența este suma inversă a perioadei, prin urmare:
f = 1 / T
În timp ce frecvența F Seamana cu frecvența unghiulară ω (pulsație), cum ar fi:
ω = 2πF
Frecvența unghiulară este exprimată în radiani / secundă în sistemul internațional, dar radianii sunt adimensionali, deci frecvența F iar frecvența unghiulară ω au aceleași dimensiuni. Rețineți că produsul ωt dă radiani ca rezultat și trebuie luat în considerare la utilizarea calculatorului pentru a obține valoarea sen ωt.
Fază
Acesta corespunde deplasării orizontale experimentate de undă, în raport cu un timp luat ca referință.
În figura următoare, valul verde este în fața valului roșu cu o singură dată td. Două unde sinusoidale sunt înăuntru fază când frecvența și faza acestuia sunt aceleași. Dacă faza diferă, atunci acestea sunt în decalaj. Undele din figura 2 sunt, de asemenea, defazate.
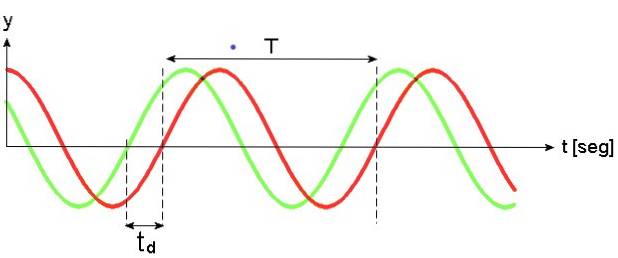
Dacă frecvența undelor este diferită, acestea vor fi în fază când faza ωt + φ este același în ambele valuri în anumite momente.
Generator de unde sinusoidale
Există multe modalități de a obține un semnal cu undă sinusoidală. Priza de acasă le oferă.
Oamenii legii Faraday
O modalitate destul de simplă de a obține un semnal sinusoidal este utilizarea legii lui Faraday. Acest lucru indică faptul că într-un circuit de curent închis, de exemplu o buclă, plasată în mijlocul unui câmp magnetic, un curent indus este generat atunci când fluxul de câmp magnetic prin el se schimbă în timp. În consecință, a tensiunea indusă sau emf indus.
Fluxul câmpului magnetic variază dacă bucla este rotită cu viteză unghiulară constantă în mijlocul câmpului creat între polii N și S ai magnetului prezentat în figură..
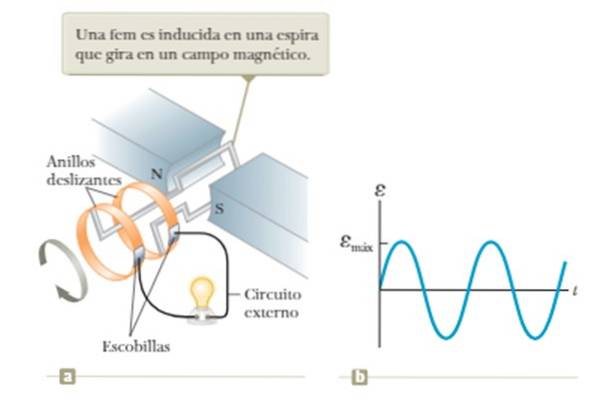
Limitarea acestui dispozitiv este dependența tensiunii obținute cu frecvența de rotație a buclei, așa cum se va vedea mai detaliat în Exemplul 1 din secțiunea Exemple de mai jos..
Oscilator Wien
O altă modalitate de a obține o undă sinusoidală, de data aceasta cu electronica, este prin oscilatorul Wien, care necesită un amplificator operațional în legătură cu rezistențe și condensatori. În acest fel, se obțin unde sinusoidale a căror frecvență și amplitudine pe care utilizatorul le poate modifica în funcție de comoditatea lor, prin ajustarea cu comutatoare..
Figura prezintă un generator de semnal sinusoidal, cu care pot fi obținute și alte forme de undă: triunghiulare și pătrate printre altele..

Cum se calculează undele sinusoidale?
Pentru a efectua calcule care implică unde sinusoidale, se folosește un calculator științific care are funcțiile trigonometrice sinus și cosinus, precum și inversele acestora. Aceste calculatoare au moduri pentru a lucra unghiurile fie în grade, fie în radiani și este ușor de convertit de la o formă la alta. Factorul de conversie este:
180 º = π radiani.
În funcție de modelul calculatorului, trebuie să navigați utilizând tasta MODE pentru a găsi opțiunea DEGREE, care vă permite să lucrați funcțiile trigonometrice în grade sau opțiunea RAD, pentru a lucra direct unghiurile în radiani.
De exemplu sin 25º = 0,4226 cu calculatorul setat în modul DEG. Conversia 25º în radiani dă 0,4363 radiani și sin 0,4363 rad = 0,425889 ≈ 0,4226.
Osciloscopul
Osciloscopul este un dispozitiv care permite afișarea semnalelor de tensiune și curent atât directe, cât și alternative. Are butoane pentru a regla dimensiunea semnalului pe o rețea așa cum se arată în figura următoare:
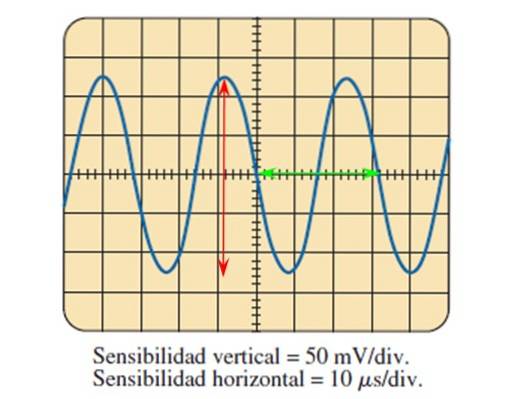
Prin imaginea oferită de osciloscop și cunoașterea reglării sensibilității în ambele axe, este posibil să se calculeze parametrii de undă care au fost descriși anterior..
Figura arată semnalul de tensiune sinusoidală în funcție de timp, în care fiecare diviziune pe axa verticală valorează 50 milivolți, în timp ce pe axa orizontală, fiecare diviziune valorează 10 microsecunde.
Amplitudinea vârf-la-vârf se găsește prin numărarea diviziunilor pe care valul le acoperă vertical, folosind săgeata roșie:
5 diviziuni sunt numărate cu ajutorul săgeții roșii, astfel încât tensiunea vârf-vârf este:
Vpp = 5 diviziuni x 50 mV / diviziune = 250 mV.
Tensiunea de vârf Vp se măsoară de pe axa orizontală, fiind de 125 mV.
Pentru a găsi perioada, se măsoară un ciclu, de exemplu cel delimitat de săgeata verde, care acoperă 3,2 diviziuni, apoi perioada este:
T = 3,2 diviziuni x 10 microsecunde / diviziune = 32 microsecunde = 32 μs
Exemple
Exemplul 1
Pentru generatorul din Fig. 3, arată din legea lui Faraday că tensiunea indusă are o formă sinusoidală. Să presupunem că bucla constă din N spire în loc de doar una, toate cu aceeași zonă A și se rotește cu viteză unghiulară constantă ω în mijlocul unui câmp magnetic B uniformă.
Soluţie
Legea lui Faraday spune că EMF indus ε este:
ε = -N (dΦB / dt)
Unde ΦB este fluxul de câmp magnetic, care va fi variabil, deoarece depinde de modul în care bucla este expusă câmpului în fiecare moment. Semnul negativ descrie pur și simplu faptul că acest EMF se opune cauzei care îl produce (legea lui Lenz). Debitul datorat unei singure viraje este:
ΦB = B.A.cos θ
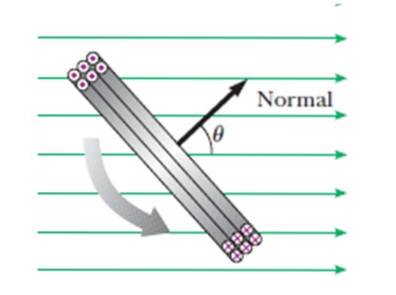
θ este unghiul pe care vectorul normal față de planul buclei îl formează cu câmpul B Pe măsură ce rotația continuă (vezi figura), acest unghi variază în mod natural ca:
θ = ωt
Astfel încât: ΦB = B.A.cos θ = B.A.cos ωt. Acum trebuie doar să derivăm această expresie cu privire la timp și cu aceasta obținem EMF indus:
ε = -N.d (B.A.cos ωt) / dt
Ca și câmpul B este uniformă și aria buclei nu variază, ele lasă în afara derivatei:
ε = -NBA. d (cos ωt) / dt = ωNBA. sen ωt
Exemplul 2
O buclă are o suprafață de 0,100 mDouă și se rotește la 60,0 turații / s, cu axa sa de rotație perpendiculară pe un câmp magnetic uniform de 0,200 T. Știind că bobina are 1000 de rotații, găsiți: a) Cf maxim care se generează, b) Orientarea bobinei în relația cu câmpul magnetic atunci când apare emf maxim indus.
Soluţie
a) CEM maxim este εmax = ωNBA
Înainte de a înlocui valorile, frecvența de 60 rotații / s trebuie transferată către unitățile sistemului internațional. Se știe că 1 revoluție este egală cu o revoluție sau 2p radiani:
60,0 rev / s = 120p radiani / s
εmax = 120p radiani x 1000 spire x 0,200 T x 0,100 mDouă = 7539,82 V = 7,5 kV
b) Când apare această valoare sen ωt = 1 Prin urmare:
ωt = θ = 90º,
Într-un astfel de caz, planul spiralei este paralel cu B, astfel încât vectorul normal la planul menționat să se formeze la 90º cu câmpul. Acest lucru se întâmplă atunci când vectorul în negru din figura 8 este perpendicular pe vectorul verde care reprezintă câmpul magnetic.
Referințe
- Boylestad, R. 2011. Introducere în analiza circuitelor. Al 12-lea. Ediție. Pearson. 327-376.
- Figueroa, D. 2005. Electromagnetism. Seria de fizică pentru știință și inginerie. Volumul 6. Editat de D. Figueroa. Universitatea Simon Bolivar. 115 și 244-245.
- Figueroa, D. 2006. Laborator de fizică 2. Editorial Equinoccio. 03-1 și 14-1.
- Valuri sinusoidale. Recuperat de pe: iessierradeguara.com
- Serway, R. 2008. Fizica pentru știință și inginerie. Volumul 2. Cengage Learning. 881- 884



Nimeni nu a comentat acest articol încă.