
Formule, caracteristici, tipuri, exemple de unde staționare
valuri staționare Sunt unde care se propagă într-un mediu limitat, mergând și venind într-o parte a spațiului, spre deosebire de undele călătoare, care la propagare se îndepărtează de sursa care le-a originat și nu se întorc la el.
Ele stau la baza sunetelor produse în instrumentele muzicale, deoarece apar ușor în corzile fixe, fie la un capăt, fie la ambele. Ele sunt, de asemenea, create în membrane strânse, cum ar fi tamburi sau în interiorul tuburilor și structurilor, cum ar fi podurile și clădirile..
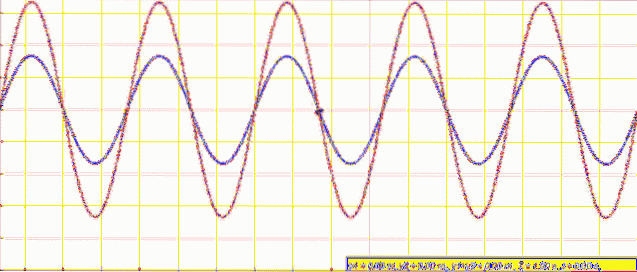
Când aveți o coardă fixă la ambele capete, cum ar fi cea a unei chitare, de exemplu, sunt create unde cu amplitudine și frecvență identice, care călătoresc în direcții opuse și se combină pentru a produce un fenomen numit interferență.
Dacă undele sunt în fază, vârfurile și văile sunt aliniate și rezultă o undă cu amplitudine de două ori. În acest caz, vorbim de interferență constructivă.
Dar dacă undele interferente sunt defazate, vârfurile unuia se întâlnesc cu văile altora și amplitudinea rezultată este zero. Este vorba atunci de interferențe distructive.
Indice articol
- 1 Formule și ecuații
- 1.1 Expresia matematică a undei staționare
- 2 Amplasarea nodurilor și a burților
- 2.1 Moduri normale pe un șir
- 2.2 Viteza și frecvența
- 3 Caracteristicile valurilor staționare
- 4 tipuri
- 4.1 Undele staționare într-o singură dimensiune
- 4.2 Undele staționare în două și trei dimensiuni
- 5 Exemple de valuri staționare
- 5.1 Corzi fixe
- 5.2 Instrumente muzicale
- 5.3 Clădiri și poduri
- 5.4 Seiches
- 5.5 Vasele de pește
- 6 Exercițiul a fost rezolvat
- 6.1 Soluția a
- 6.2 Soluția b
- 6.3 Soluția c
- 7 Referințe
Formule și ecuații
Elementele principale ale undei care o reprezintă în spațiu și timp sunt amplitudinea sa A, lungimea de undă λ și frecvența unghiulară ω.
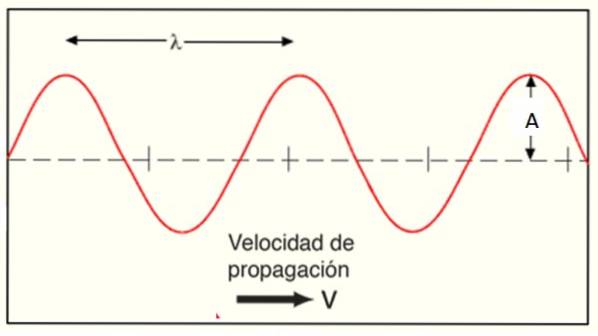
În reprezentarea matematică se preferă utilizarea k, decât a numărul de undă sau de câte ori apare unda pe unitatea de lungime. De aceea este definit prin lungimea de undă λ care este distanța dintre două văi sau două creste:
k = 2π / λ
In timp ce frecvența unghiulară se referă la perioada sau durata unei oscilații complete, cum ar fi:
ω = 2π / T
Și, de asemenea, frecvența f este dată de:
f = ω / 2π
Prin urmare:
f = 1 / T
De asemenea, valurile se mișcă cu viteză v in conformitate:
v = λ.f
Expresia matematică a undei staționare
Matematic putem exprima o undă folosind funcția sinus sau funcția cosinus. Să presupunem că avem unde de amplitudine egală A, lungimea de undă λ și frecvența ω, care se propagă de-a lungul unui șir și în direcții opuse:
Da1 = Un păcat (kx - ωt)
DaDouă = Un păcat (kx + ωt)
La adăugarea lor găsim unda rezultată șiR:
DaR = și1 + DaDouă = Un păcat (kx - ωt) + Un păcat (kx + ωt)
Există o identitate trigonometrică pentru a găsi suma:
sin α + sin β = 2 sin (α + β) / 2. cos (α - β) / 2
Prin această identitate, unda rezultată yR rămâne:
DaR = [2A sin kx]. cos ωt
Localizarea nodurilor și a burților
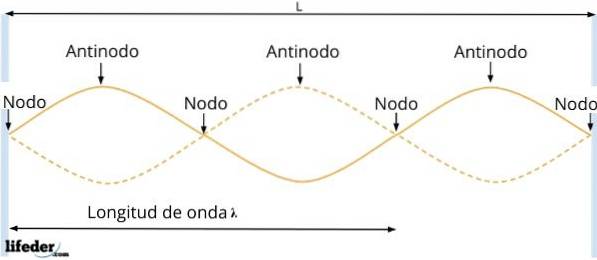
Unda rezultată are amplitudine AR = 2Asen kx, care depinde de poziția particulei. Apoi, în punctele pentru care sin kx = 0, amplitudinea undei dispare, adică nu există vibrații.
Aceste puncte sunt:
kx = π, 2π, 3π ...
Deoarece k = 2 π / λ:
(2 π / λ) x = π, 2π, 3π ...
x = λ / 2, λ, 3λ / 2 ...
Interferența distructivă apare în astfel de puncte și se numește noduri. Acestea sunt separate de o distanță egală cu λ / 2, după cum s-a dedus din rezultatul anterior.
Și între două noduri consecutive sunt antinodele sau burti, în care amplitudinea undei este maximă, deoarece interferența constructivă apare acolo. Ele apar atunci când:
sin kx = ± 1
kx = ± π / 2, 3π / 2, 5π / 2 ...
Din nou k = 2 π / λ și apoi:
x = λ / 4, 3λ / 4, 5λ / 4, ...
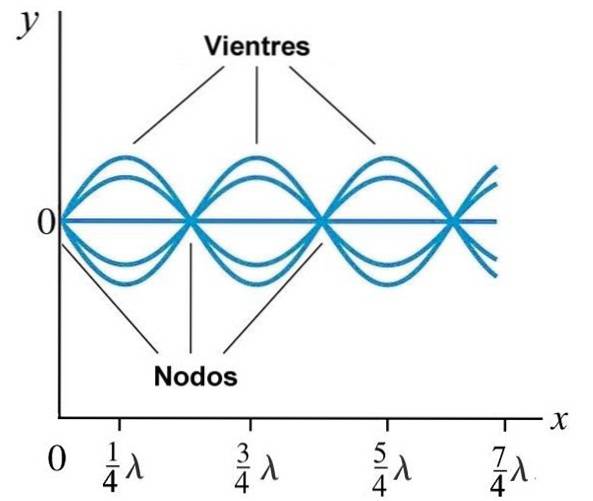
Moduri normale pe un șir
Condițiile de graniță din șir determină cum sunt lungimile de undă și frecvențele. Dacă un șir de lungime L este fixat la ambele capete, acesta nu poate vibra cu nicio frecvență, deoarece punctele în care șirul este fixat sunt deja noduri.
Mai mult decât atât, separarea între nodurile adiacente este λ / 2, iar între nod și burta este λ / 4, în acest fel numai pentru anumite lungimi de undă se produc unde staționare: cele în care un număr întreg n de λ / 2 se încadrează în:
(λ / 2) = L, cu n = 1, 2, 3, 4 ... .
Prin urmare:
λ = 2L / n
Armonice
Se numesc diferitele valori pe care le ia λ armonice. Astfel avem:
-Prima armonică: λ = 2L
-A doua armonică: λ = L
-A treia armonică: λ = 2 L / 3
-Al patrulea armonic: λ = L / 2
Și așa mai departe.
Viteza și frecvența
Chiar dacă unda staționară nu pare să se miște, ecuația este încă valabilă:
v = λ. F
Prin urmare:
v = (2L / n). F
f = nv / 2L
Acum, se poate arăta că viteza cu care o undă se deplasează într-un șir depinde de tensiunea T din ea și de densitatea sa liniară de masă μ (masă pe unitate de lungime) ca:

Prin urmare:

Caracteristicile valurilor staționare
-Când undele sunt staționare, unda rezultată nu se propagă la fel ca componentele sale, care merg de la o parte la alta. Există puncte în care y = 0 deoarece nu există vibrații: nodurile, cu alte cuvinte, amplitudinea AR devine zero.
-Expresia matematică a unei unde staționare constă în produsul unei părți spațiale (care depinde de coordonatele x sau coordonatele spațiale) și o parte temporală.
-Între noduri, unda neagră rezultată oscilează într-un singur loc, în timp ce undele care merg dintr-o parte în alta sunt defazate acolo..
-Energia nu este transportată chiar la noduri, deoarece aceasta este proporțională cu pătratul amplitudinii, dar este prinsă între noduri.
-Distanța dintre nodurile adiacente este jumătate din lungimea de undă.
-Punctele în care coarda este fixată sunt, de asemenea, considerate noduri..
Tipuri
Undele staționare într-o singură dimensiune
Undele dintr-un șir fix sunt exemple de unde staționare într-o dimensiune, a căror descriere matematică le-am oferit în secțiunile anterioare..
Undele staționare în două și trei dimensiuni
Undele staționare pot fi, de asemenea, prezentate în două și trei dimensiuni, descrierea lor matematică fiind puțin mai complexă.
Exemple de valuri staționare
Frânghii fixe
-O frânghie fixată la un capăt care este oscilată manual sau cu un piston pe celălalt generează valuri staționare de-a lungul lungimii sale.
Instrumente muzicale

-Cântarea instrumentelor cu coarde, cum ar fi chitara, harpa, vioara și pianul creează, de asemenea, unde permanente, deoarece au corzi ajustate la diferite tensiuni și fixate la ambele capete.
Undele staționare sunt, de asemenea, create în tuburi cu aer, cum ar fi tuburile de organe..
Clădiri și poduri
Valurile staționare apar în structuri precum poduri și clădiri. Un caz notabil a fost cel al podului suspendat Tacoma Narrows de lângă orașul Seattle, Statele Unite. La scurt timp după ce a fost inaugurat în 1940, acest pod s-a prăbușit din cauza valurilor staționare create în interior de vânt..
Frecvența vântului a fost asociată cu frecvența naturală a podului, creându-se unde staționare, care au crescut în amplitudine până când podul s-a prăbușit. Fenomenul este cunoscut sub numele de rezonanță.
Seiches
În porturi există un fenomen foarte curios numit seiche, în care valurile mării produc oscilații mari. Acest lucru se datorează faptului că apele din port sunt destul de închise, deși apele oceanice pătrund din când în când prin intrarea în port..
Apele portului se mișcă cu propria lor frecvență, la fel ca cele ale oceanului. Dacă ambele ape sunt egale cu frecvențele lor, un val staționar mare este produs prin rezonanță, așa cum sa întâmplat cu podul Tacoma..
seiches Ele pot apărea, de asemenea, în lacuri, rezervoare, piscine și alte corpuri de apă cu suprafață limitată..
Rezervoare de pește
Valurile staționare pot fi create într-un rezervor de pești transportat de o persoană, dacă frecvența cu care merge persoana este egală cu frecvența legănării apei.
Exercițiul a fost rezolvat
O coardă de chitară are L = 0,9 m și o densitate de masă liniară μ = 0,005 kg / m. Este supus la 72 N de tensiune și modul său de vibrație este cel prezentat în figură, cu amplitudine 2A = 0,5 cm.
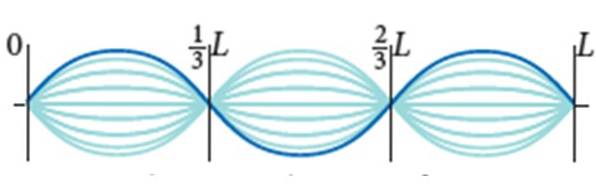
Găsi:
a) Viteza de propagare
b) Frecvența undelor
c) Ecuația undei staționare corespunzătoare.
Solutie la
Prin:

Este obținut;
v = [72 N / (0,005 kg / m)]1/2 = 120 m / s.
Soluția b
Distanța dintre două noduri adiacente este λ / 2, prin urmare:
(2/3) L - (1/3) L = λ / 2
(1/3) L = λ / 2
λ = 2L / 3 = 2 x 0,90 m / 3 = 0,60 m.
Din moment ce v = λ.f
f = (120 m / s) / 0,60 m = 200 s-1= 200 Hz.
Soluția c
Ecuația este:
DaR = [2A sin kx]. cos ωt
Trebuie să înlocuim valorile:
k = 2π / λ = k = 2π / 0,60 m = 10 π / 3
f = ω / 2π
ω = 2π x 200 Hz = 400 π Hz.
Amplitudinea 2A este deja dată de enunțul:
2A = 0,5 cm = 5 x 10 -3 m.
Prin urmare:
DaR = 5 x 10 -3 m. sin [(10π / 3) x]. cos (400πt) =
= 0,5 cm. sin [(10π / 3) x]. cos (400πt)
Referințe
- Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 7. Valurile și fizica cuantică. Editat de Douglas Figueroa (USB).
- Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7. Ed. Cengage Learning.
- Tipler, P. (2006) Fizică pentru știință și tehnologie. Ediția a 5-a Volumul 1. Editorial Reverté.
- Wikipedia. Seiche. Recuperat de pe: es.wikipedia.org.


Nimeni nu a comentat acest articol încă.