
Formule ortoedronice, zonă, volum, diagonală, exemple
ortoedru Este o figură geometrică volumetrică sau tridimensională care se caracterizează prin faptul că are șase fețe dreptunghiulare, astfel încât fețele opuse sunt în planuri paralele și sunt dreptunghiuri identice sau congruente. Pe de altă parte, fețele adiacente unei fețe date sunt în planuri perpendiculare pe cea a feței inițiale..
De asemenea, poate fi luat în considerare ortoedru ca o prismă ortogonală cu o bază dreptunghiulară, în care unghiuri diedre formate din planurile a două fețe adiacente unei muchii comune, acestea măsoară 90º. Unghiul diedru dintre două fețe se măsoară pe intersecția fețelor cu un plan perpendicular comun acestora.
La fel, ortoedrul este un dreptunghi paralelipiped, întrucât așa se definește paralelipipedul ca figura volumetrică a șase fețe, care sunt paralele două câte două.
În orice paralelipiped fețele sunt paralelograme, dar în paralelipiped dreptunghiular fețele trebuie să fie dreptunghiulare.
Indice articol
- 1 Părți ale ortoedronului
- 2 formule ortoedronice
- 2.1 Zona
- 2.2 Volum
- 2.3 Diagonală internă
- 3 Exemple
- 3.1 - Exemplul 1
- 3.2 - Exercițiul 2
- 4 Referințe
Părți ale ortoedrului
Părțile unui poliedru, cum ar fi ortoedrul, Sunt:
-Margini
-Vârfuri
-Fețe
Unghiul dintre două margini ale unei fețe a ortoedronului coincide cu unghiul diedru format de celelalte două fețe ale acesteia adiacente fiecărei margini, formând un unghi drept. Următoarea imagine clarifică fiecare concept:
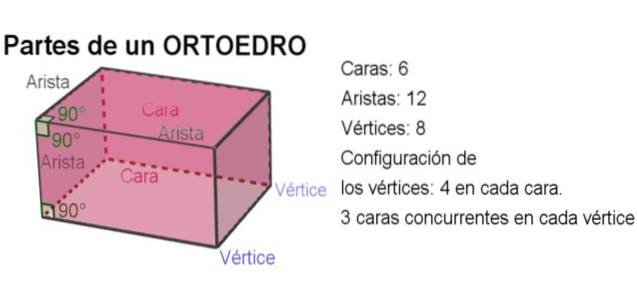
-În total, un ortoedru are 6 fețe, 12 margini și 8 vârfuri..
-Unghiul dintre oricare două margini este un unghi drept.
-Unghiul diedru dintre oricare două fețe este, de asemenea, corect.
-În fiecare față există patru vârfuri și în fiecare vârf concurează trei fețe reciproc ortogonale.
Formule ortoedronice
Zonă
Suprafața sau aria unui ortoedru este suma ariilor fețelor lor.
Dacă cele trei margini care se întâlnesc la un vârf au măsuri a, b și c, așa cum se arată în Figura 3, atunci fața frontală are zonă c⋅b iar fața inferioară are, de asemenea, zona c⋅b.
Apoi cele două fețe laterale au suprafață a⋅b fiecare. Și, în cele din urmă, fețele de podea și tavan au suprafață Î.Hr. fiecare.
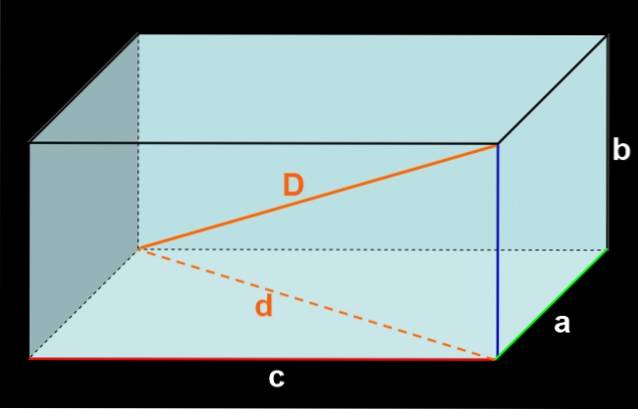
Adăugarea zonei tuturor fețelor oferă:
A = 2⋅c⋅b + 2⋅a⋅b + 2⋅a⋅c
Luând un factor comun și ordonând termenii:
A = 2⋅ (a⋅b + b⋅c + c⋅a)
Volum
Dacă ortoedrul este considerat o prismă, atunci volumul său se calculează după cum urmează:
Volum = Suprafața bazei prismei x înălțimea prismei
În acest caz, podeaua de dimensiuni este luată ca bază dreptunghiulară c Da la, atunci aria bazei este c⋅a.
Înălțimea este dată de lungime b de la marginile ortogonale la fețele laterale la Da c.
Înmulțind aria bazei (Î.Hr.) după înălțime b tu ai volumul V al ortoedrului:
V = a⋅b⋅c
Diagonală internă
Într-un ortoedru există două tipuri de diagonale: diagonalele externe și diagonalele interne.
Diagonalele exterioare sunt pe fețele dreptunghiulare, în timp ce diagonalele interne sunt segmentele care unesc două vârfuri opuse, fiind înțelese prin vârfuri opuse cele care nu au nici o margine.
Într-un ortoedru există patru diagonale interne, toate de aceeași măsură. Lungimea diagonalelor interne poate fi obținută prin aplicarea teoremei pitagoreice pentru triunghiuri dreptunghiulare.
Lungimea d a diagonalei exterioare a feței de podea a ortoedronului îndeplinește relația pitagorică:
dDouă = aDouă + cDouă
În mod similar, diagonala interioară a măsurii D îndeplinește relația pitagorică:
DDouă = dDouă + bDouă.
Combinând cele două expresii anterioare pe care le avem:
DDouă = aDouă + cDouă + bDouă.
În cele din urmă, lungimea oricăreia dintre diagonalele interne ale ortoedronului este dată de următoarea formulă:
D = √ (aDouă + bDouă + cDouă ).
Exemple
- Exemplul 1
Un zidar construiește un rezervor în formă de ortoedru ale cărui dimensiuni interne sunt: 6 m x 4 m în bază și 2 m în înălțime. Întrebă:
a) Determinați suprafața interioară a rezervorului dacă acesta este complet deschis în partea de sus.
b) Calculați volumul spațiului interior al rezervorului.
c) Aflați lungimea unei diagonale interioare.
d) Care este capacitatea rezervorului în litri?
Solutie la
Vom lua dimensiunile bazei dreptunghiulare a = 4 m și c = 6 m și înălțimea ca b = 2 m
Aria unui ortoedru cu dimensiunile date este dată de următoarea relație:
A = 2⋅ (a⋅b + b⋅c + c⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)
Și anume:
A = 2⋅ (8 mDouă + 12 mDouă + 24 mDouă) = 2⋅ (44 mDouă) = 88 mDouă
Rezultatul anterior este zona ortoedronului închis cu dimensiunile date, dar din moment ce este un rezervor complet descoperit în partea sa superioară, pentru a obține suprafața pereților interiori a rezervorului, zona capacului lipsă trebuie scăzut, adică:
c⋅a = 6 m ⋅ 4 m = 24 mDouă.
În cele din urmă, suprafața interioară a rezervorului va fi: S = 88 mDouă - 24 mDouă = 64 mDouă.
Soluția b
Volumul interior al rezervorului este dat de volumul unui ortoedru al dimensiunilor interioare ale rezervorului:
V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m3.
Soluția c
Diagonala interioară a unui octaedru cu dimensiunile interiorului rezervorului are o lungime D dată de:
√ (laDouă + bDouă + cDouă ) = √ ((4 m)Două + (2 m)Două + (6 m)Două )
Efectuând operațiunile indicate avem:
D = √ (16 mDouă + 4 mDouă + 36 mDouă ) = √ (56 mDouă) = 2√ (14) m = 7,48 m.
Soluția d
Pentru a calcula capacitatea rezervorului în litri, este necesar să știți că volumul unui decimetru cub este egal cu capacitatea unui litru. Acesta a fost calculat anterior în volum în metri cubi, dar trebuie transformat în decimetri cubi și apoi în litri:
V = 48 m3 = 48 (10 dm)3 = 4.800 dm3 = 4.800 L
- Exercițiul 2
Un acvariu de sticlă are o formă cubică cu o latură de 25 cm. Determinați aria în mDouă, volumul în litri și lungimea unei diagonale interioare în cm.
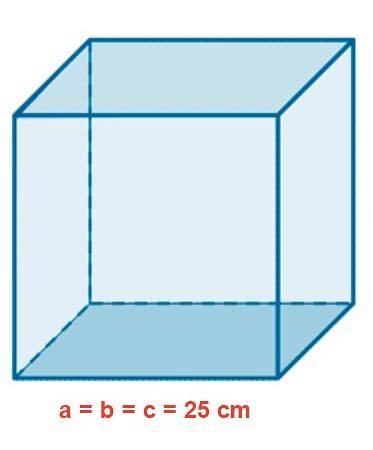
Soluţie
Suprafața este calculată utilizând aceeași formulă ortoedronă, dar ținând cont de faptul că toate dimensiunile sunt identice:
A = 2⋅ (3 a⋅a) = 6⋅ aDouă = 6⋅ (25 cm)Două = 1.250 cmDouă
Volumul cubului este dat de:
V = a3 = (25 cm)3 = 15.625 cm3 = 15.625 (0,1 dm)3 = 15.625 dm3 = 15.625 L.
Lungimea D a diagonalei interioare este:
D = √ (3aDouă) = 25√ (3) cm = 43,30 cm.
Referințe
- Arias J. GeoGebra: Prism. Recuperat de pe: youtube.com.
- Calculus.cc. Exerciții și probleme rezolvate de zone și volume. Recuperat de la: calculo.cc.
- Salvador R. Piramida + ortoedru cu GEOGEBRA (IHM). Recuperat de pe: youtube.com
- Weisstein, Eric. „Orthohedron”. MathWorld. Wolfram Research.
- Wikipedia. Ortohedron Recuperat de pe: es.wikipedia.com



Nimeni nu a comentat acest articol încă.