Într-o proces izobaric, presiunea P a unui sistem rămâne constantă. Prefixul „iso” provine din greacă și este folosit pentru a desemna că ceva rămâne constant, în timp ce „baros”, tot din greacă, înseamnă greutate.
Procesele izobarice sunt foarte tipice atât în containere închise, cât și în spații deschise, fiind ușor de localizat în natură. Prin aceasta înțelegem că sunt posibile modificări fizice și chimice la suprafața pământului sau reacții chimice în recipientele deschise către atmosferă..
Câteva exemple sunt obținute prin încălzirea unui balon umplut cu aer la soare, gătirea, fierberea sau congelarea apei, aburul generat în cazane sau procesul de ridicare a unui balon cu aer cald. Mai târziu vom oferi o explicație a acestor cazuri.
Indice articol
Să derivăm o ecuație pentru procesul izobaric presupunând că sistemul în studiu este un gaz ideal, un model destul de potrivit pentru aproape orice gaz la mai puțin de 3 atmosfere de presiune. Particulele de gaz ideale se mișcă la întâmplare, ocupând întregul volum al spațiului care le conține fără a interacționa între ele..
Dacă gazul ideal închis într-un cilindru prevăzut cu un piston mobil este lăsat să se extindă lent, se poate presupune că particulele sale sunt în echilibru în orice moment. Apoi gazul se exercită asupra pistonului zonei LA o forță F de mărime:
F = p.A
Unde p este presiunea gazului. Această forță exercită muncă producând o deplasare infinitesimală dx pe pistonul dat de:
dW = Fdx = pA.dx
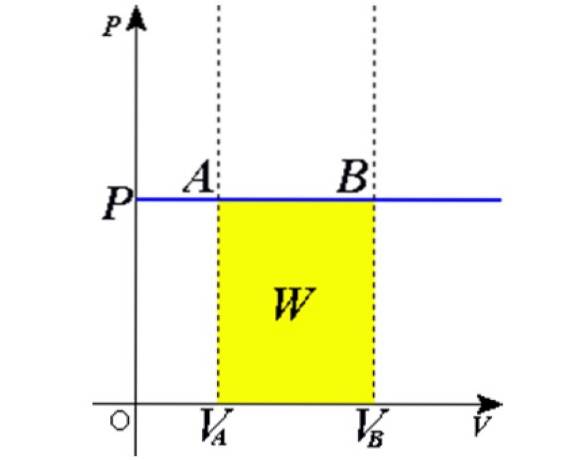
Ca produs Adx este un diferențial de volum dV, atunci dW = pdV. Rămâne să se integreze ambele părți din volumul inițial VLA până la volumul final VB pentru a obține lucrul total realizat de gaz:
Situația descrisă este verificată experimental prin închiderea unui gaz în interiorul unui cilindru prevăzut cu un piston mobil, așa cum se arată în figurile 2 și 3. O greutate de masă M este plasată pe piston, a cărei greutate este direcționată în jos, în timp ce gazul exercită o forță ascendentă datorită presiunii P produsă pe piston.
Deoarece pistonul se poate mișca liber, volumul pe care îl ocupă gazul se poate modifica fără probleme, dar presiunea rămâne constantă. Adăugarea presiunii atmosferice PATM, care exercită și o forță descendentă, avem:
Mg - P.A + PATM . A = constantă
Prin urmare: P = (Mg / A) + PATM nu variază decât dacă M și astfel greutatea sunt modificate. Prin adăugarea căldurii în butelie, gazul se va extinde prin creșterea volumului sau se va contracta la extragerea căldurii..
Ecuația de stare ideală a gazului raportează variabilele de importanță: presiunea P, volumul V și temperatura T:
P.V = n .R.T
Aici n reprezintă numărul de moli și R este constanta de gaz ideală (valabilă pentru toate gazele), care se calculează prin înmulțirea constantei lui Boltzmann cu numărul lui Avogadro, rezultând:
R = 8,31 J / mol K
Când presiunea este constantă, ecuația stării poate fi scrisă ca:
V / T = nR / P
Dar nR / P este constant, deoarece n, R și P sunt. Deci, atunci când sistemul trece de la starea 1 la starea 2, apare următoarea proporție, cunoscută și sub numele de legea lui Charles:
V1/ T1 = VDouă/ TDouă
Înlocuind în W = PΔV, munca făcută pentru a trece de la starea 1 la starea 2 se obține, în ceea ce privește constantele și variația temperaturii, ușor de măsurat cu un termometru:
W1 → 2 = nR (TDouă - T1) = nR.ΔT
Pe de altă parte, prima lege a termodinamicii afirmă că:
∆U = Q - W
Aceasta înseamnă că adăugarea unei anumite cantități de căldură Q la gaz mărește energia internă ∆U și crește vibrațiile moleculelor sale. În acest fel, gazul se extinde și funcționează prin mișcarea pistonului, așa cum am spus mai înainte..
Într-un gaz ideal monatomic și variația energiei interne ∆U, care include atât energia cinetică, cât și energia potențială a moleculelor sale, este:
∆U = (3/2)nR ΔT
În cele din urmă, combinăm expresiile pe care le-am obținut într-una:
Î = ∆U + W = (3/2)nR ΔT + nR∆T = (5/2) nR ΔT
Alternativ, Q poate fi rescris în termeni de masă m, diferența de temperatură și o nouă constantă numită căldura specifică a gazului la presiune constantă, prescurtat cp, ale căror unități sunt J / mol K:
Q = m cp ∆T
Nu toate procesele izobarice se desfășoară în containere închise. De fapt, nenumărate procese termodinamice de tot felul apar la presiunea atmosferică, deci procesele izobarice sunt foarte frecvente în natură. Aceasta include modificări fizice și chimice la suprafața pământului, reacții chimice în vasele deschise către atmosferă și multe altele..
Pentru ca procesele izobarice să aibă loc în sisteme închise, limitele lor trebuie să fie suficient de flexibile pentru a permite modificări de volum fără presiuni variabile.
Așa s-a întâmplat în experimentul pistonului care s-a mișcat ușor pe măsură ce gazul s-a extins. Același lucru se întâmplă înglobând un gaz într-un balon de petrecere sau un balon cu aer cald.
Aici avem mai multe exemple de procese izobarice:
Apa clocotită pentru ceai sau sosurile de gătit în recipiente deschise sunt exemple bune de procese izobarice, deoarece toate au loc la presiune atmosferică..
Pe măsură ce apa este încălzită, temperatura și volumul cresc și dacă se continuă adăugarea de căldură, se ajunge în cele din urmă la punctul de fierbere, în care are loc schimbarea de fază a apei din lichid în vapori de apă. În timp ce se întâmplă acest lucru, temperatura rămâne constantă și la 100 ° C..
Pe de altă parte, înghețarea apei este, de asemenea, un proces izobaric, indiferent dacă are loc într-un lac în timpul iernii sau frigiderul de acasă..
Un alt exemplu de proces izobaric este modificarea volumului unui balon umflat cu aer atunci când este lăsat expus Soarelui. Primul lucru dimineața, când încă nu este foarte cald, balonul are un anumit volum..
Pe măsură ce timpul trece și temperatura crește, balonul se încălzește, de asemenea, crescându-și volumul și toate acestea apar la presiune constantă. Materialul balonului este un bun exemplu de bordură suficient de flexibilă astfel încât aerul din interiorul său, când este încălzit, să se extindă fără a modifica presiunea.
Experiența poate fi realizată și prin ajustarea balonului neumflat în gura unei sticle de sticlă umplută cu o treime de apă, care este încălzită la bain-marie. De îndată ce apa este încălzită, balonul se umflă imediat, dar trebuie avut grijă să nu se încălzească prea mult pentru a nu exploda..
Este o navă plutitoare fără propulsie, care folosește curenții de aer pentru a transporta oameni și obiecte. Balonul este de obicei umplut cu aer cald, care, fiind mai rece decât aerul înconjurător, crește și se extinde provocând creșterea balonului..
Deși curenții de aer dirijează balonul, acesta are arzătoare care sunt activate pentru a încălzi gazul atunci când se dorește să urce sau să mențină altitudinea și să se dezactiveze la coborâre sau aterizare. Toate acestea se întâmplă la presiunea atmosferică, presupusă constantă la o anumită înălțime nu departe de suprafață..
Aburul este generat în cazane prin încălzirea apei și menținerea constantă a presiunii. Ulterior, acest abur îndeplinește o treabă utilizabilă, de exemplu, generând electricitate în centralele termoelectrice sau activând alte mecanisme, cum ar fi locomotive și pompe de apă..
Există 40 de litri de gaz la o temperatură de 27 ° C. Găsiți creșterea volumului atunci când se adaugă căldură izobaric până la 100 ° C.
Legea lui Charles este folosită pentru a determina volumul final, dar Atenţie: temperaturile trebuie exprimate în kelvin, adăugând doar 273 K la fiecare:
27 ºC = 27 + 273 K = 300 K
100 ºC = 100 + 273 K = 373 K
Din:
V1/ T1 = VDouă/ TDouă ⇒ VDouă = TDouă(V1/ T1) = 373 ºC (40 L / 300 K) = 49,7 L
În cele din urmă, creșterea volumului este VDouă - V1 = 49,7 L - 40 L = 9,7 L.
Livrat 5,00 x 103 J de energie la un gaz ideal pentru a efectua 2,00 x 103 J lucrează la mediul său într-un proces izobaric. Se cere să găsiți:
a) Schimbarea energiei interne a gazului.
b) Modificarea volumului, dacă acum energia internă scade cu 4,50 x 103 J și 7,50 x 10 sunt evacuate3 J al sistemului, având în vedere presiunea constantă de 1,01 x 105 Pa.
Folosit ∆U = Q - W iar valorile date în enunț sunt înlocuite: Q = 5,00 x 103 J și W = 2,00 x 103 J:
=5,00 x 103 J - 2,00 x 103 J = 3,00 x 103 J
Prin urmare, energia internă a gazului crește cu 3,00 x 103 J.
Modificarea volumului se regăsește în lucrările efectuate: W = P∆V:
∆U = Q - W = Q - P∆V
Afirmația afirmă că energia internă scade, prin urmare: ∆U= -4,50 x 103 J. De asemenea, ne spune că o anumită cantitate de căldură este expulzată: Q = -7,50 x 103 J. În ambele cazuri, semnul negativ reprezintă scăderea și pierderea, deci:
-4,50 x 103 J = -7,50 x 103 J - P∆V
Unde P = 1,01 x 105 Pa. Deoarece toate unitățile sunt în sistemul internațional, continuăm să soluționăm schimbarea volumului:
∆V = (-4,50 x 103 J +7,50 x 103 J) / (- 1,01 x 105 Pa) = -2,97 x 10-Două m3
Deoarece modificarea volumului este negativă, înseamnă că volumul a scăzut, adică sistemul s-a contractat.
Nimeni nu a comentat acest articol încă.