
Proprietăți, aplicații și exerciții transversale ale produselor
produs încrucișat sau produs vector este un mod de a multiplica doi sau mai mulți vectori. Există trei moduri de a multiplica vectorii, dar niciuna dintre acestea nu este multiplicare în sensul obișnuit al cuvântului. Una dintre aceste forme este cunoscută sub numele de produs vector, ceea ce ne dă drept rezultat un al treilea vector.
Produsul încrucișat, care se mai numește produs încrucișat sau produs exterior, are proprietăți algebrice și geometrice diferite. Aceste proprietăți sunt foarte utile, mai ales în studiul fizicii..

Indice articol
- 1 Definiție
- 2 Proprietăți
- 2.1 Proprietatea 1
- 2.2 Proprietatea 2
- 2.3 Proprietatea 3
- 2.4 Proprietatea 4 (produs cu triplu punct)
- 2.5 Proprietatea 5 (produs vector triplu)
- 2.6 Proprietatea 6
- 2.7 Proprietatea 7
- 2.8 Proprietatea 8
- 3 Aplicații
- 3.1 Calculul volumului unui paralelipiped
- 4 exerciții rezolvate
- 4.1 Exercițiul 1
- 4.2 Exercițiul 2
- 5 Referințe
Definiție
O definiție formală a produsului vector este următoarea: dacă A = (a1, a2, a3) și B = (b1, b2, b3) sunt vectori, atunci produsul vector al lui A și B, pe care îl vom denumi AxB, este:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
Datorită notației AxB, se citește ca „O cruce B”.
Un exemplu de utilizare a produsului exterior este că dacă A = (1, 2, 3) și B = (3, -2, 4) sunt vectori, atunci folosind definiția unui produs vector avem:
AxB = (1, 2, 3) x (3, -2, 4) = (2 * 4 - 3 * (- 2), 3 * 3 - 1 * 4, 1 * (- 2) - 2 * 3)
AxB = (8 + 6, 9 - 4, - 2 - 6) = (14, 5, - 8).
Un alt mod de exprimare a produsului vector este dat de notația determinanților.
Calculul unui determinant de ordinul doi este dat de:
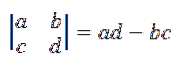
Prin urmare, formula pentru produsul încrucișat dată în definiție poate fi rescrisă după cum urmează:
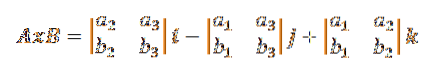
Acest lucru este de obicei simplificat într-un determinant de ordinul trei, după cum urmează:
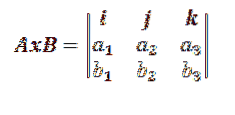
Unde i, j, k reprezintă vectorii care formează baza lui R3.
Folosind acest mod de exprimare a produsului încrucișat, avem în vedere că exemplul anterior poate fi rescris ca:
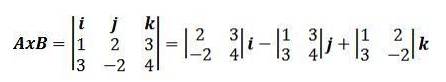
Proprietăți
Unele proprietăți pe care le are produsul vector sunt următoarele:
Proprietatea 1
Dacă A este orice vector în R3, noi trebuie sa:
- AxA = 0
- Ax0 = 0
- 0xA = 0
Aceste proprietăți sunt ușor de verificat folosind doar definiția. Dacă A = (a1, a2, a3) avem:
AxA = (a2a3 - a3a2, a3a1 - a1a3, a1a2 - a2a1) = (0, 0, 0) = 0.
Ax0 = (a2 * 0 - a3 * 0, a3 * 0 - a1 * 0, a1 * 0 - a2 * 0) = (0, 0, 0) = 0.
Dacă i, j, k reprezintă baza unitară a lui R3, le putem scrie astfel:
i = (1, 0, 0)
j = (0, 1, 0)
k = (0, 0, 1)
Deci, avem următoarele proprietăți:
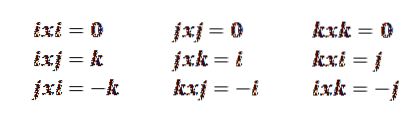
Ca regulă mnemonică, următorul cerc este adesea folosit pentru a ne aminti aceste proprietăți:
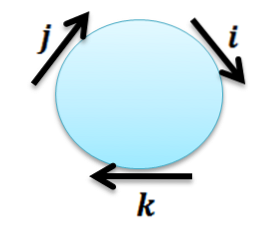
Acolo trebuie să observăm că orice vector cu el însuși dă vectorul 0 ca rezultat, iar restul produselor pot fi obținute cu următoarea regulă:
Produsul încrucișat a doi vectori consecutivi în direcția acelor de ceasornic dă următorul vector; și atunci când este luat în considerare în sens invers acelor de ceasornic, rezultatul este următorul vector cu semn negativ.
Datorită acestor proprietăți putem vedea că produsul vector nu este comutativ; de exemplu, rețineți că i x j ≠ j x i. Următoarea proprietate ne spune cum sunt legate în general AxB și BxA.
Proprietatea 2
Dacă A și B sunt vectori ai lui R3, noi trebuie sa:
AxB = - (BxA).
Demonstrație
Dacă A = (a1, a2, a3) și B = (b1, b2, b3), prin definiția produsului extern avem:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
= (- 1) (a3b2 - a2b3, a1b3 - a3b1, a2b1 - a1b2)
= (- 1) (BxA).
De asemenea, putem vedea că acest produs nu este asociat cu următorul exemplu:
ix (ixj) = ixk = - j but (ixi) xj = 0xj = 0
Din aceasta putem vedea că:
ix (ixj) ≠ (ixi) xj
Proprietatea 3
Dacă A, B, C sunt vectori ai lui R3 și r este un număr real, următoarele sunt adevărate:
- Ax (B + C) = AxB + AxC
- r (AxB) = (rA) xB = Ax (rB)
Datorită acestor proprietăți putem calcula produsul vector folosind legile algebrei, cu condiția respectării ordinii. De exemplu:
Dacă A = (1, 2, 3) și B = (3, -2, 4), le putem rescrie pe baza canonică a lui R3.
Astfel, A = i + 2j + 3k și B = 3i - 2j + 4k. Apoi, aplicând proprietățile anterioare:
AxB = (i + 2j + 3k) x (3i - 2j + 4k)
= 3 (ixi) - 2 (ixj) + 4 (ixk) + 6 (jxi) - 4 (jxj) + 8 (jxk) + 9 (kxi) - 6 (kxj) +12 (kxk)
= 3 (0) - 2 (k) + 4 (- j) + 6 (- k) - 4 (0) + 8 (i) + 9 (j) - 6 (- i) +12 (0)
= - 2k - 4j - 6k + 8i + 9j + 6i = 14i + 5j - 4k
= (14, 5, - 8).
Proprietatea 4 (produs cu triplu punct)
După cum am menționat la început, există alte modalități de a multiplica vectori în afară de produsul vector. Una dintre aceste modalități este produsul scalar sau produsul interior, care este notat ca A ∙ B și a cărui definiție este:
Dacă A = (a1, a2, a3) și B = (b1, b2, b3), atunci A ∙ B = a1b1 + a2b2 + a3b3
Proprietatea care leagă ambele produse este cunoscută sub numele de produs triplu scalar.
Dacă A, B și C sunt vectori ai lui R3, apoi A ∙ BxC = AxB ∙ C
De exemplu, să vedem că, având în vedere A = (1, 1, - 2), B = (- 3, 4, 2) și C = (- 5, 1, - 4), această proprietate este îndeplinită.
BxC = - 3k - 12j + 20k - 16i - 10j - 2i = - 18i - 22j + 17k
A ∙ BxC = (1, 1, - 2) ∙ (- 18, - 22, 17) = (1) (- 18) + (1) (- 22) + (- 2) (17) = - 74
Pe de altă parte:
AxB = 4k - 2j + 3k + 2i + 6j + 8i = 10i + 4j + 7k
AxB ∙ C = (10, 4, 7) ∙ (- 5, 1, - 4) = (10) (- 5) + (4) (1) + (7) (- 4) = - 74
Un alt produs triplu este Ax (BxC), care este cunoscut sub numele de produs triplu vector..
Proprietatea 5 (produs vector triplu)
Dacă A, B și C sunt vectori ai lui R3, atunci:
Ax (BxC) = (A ∙ C) B - (A ∙ B) C
De exemplu, să vedem că, având în vedere A = (1, 1, - 2), B = (- 3, 4, 2) și C = (- 5, 1, - 4), această proprietate este îndeplinită.
Din exemplul anterior știm că BxC = (- 18, - 22, 17). Să calculăm Ax (BxC):
Ax (BxC) = - 22k - 17j + 18k + 17i + 36j - 44i = - 27i + 19j - 4k
Pe de altă parte, trebuie să:
A ∙ C = (1, 1, - 2) ∙ (- 5, 1, - 4) = (1) (- 5) + (1) (1) + (- 2) (- 4) = - 5 + 1 + 8 = 4
A ∙ B = (1, 1, - 2) ∙ (- 3, 4, 2) = (1) (- 3) + (1) (4) + (- 2) (2) = - 3 + 4 - 4 = - 3
Astfel, trebuie să:
(A ∙ C) B - (A ∙ B) C = 4 (- 3, 4, 2) + 3 (- 5, 1, - 4) = (- 12, 16, 8) + (- 15, 3, - 12) = (- 27,19, -4)
Proprietatea 6
Este una dintre proprietățile geometrice ale vectorilor. Dacă A și B sunt doi vectori în R3 și ϴ este unghiul format între acestea, atunci:
|| AxB || = || A |||| B || sin (ϴ), unde || ∙ || denotă modulul sau magnitudinea unui vector.
Interpretarea geometrică a acestei proprietăți este următoarea:
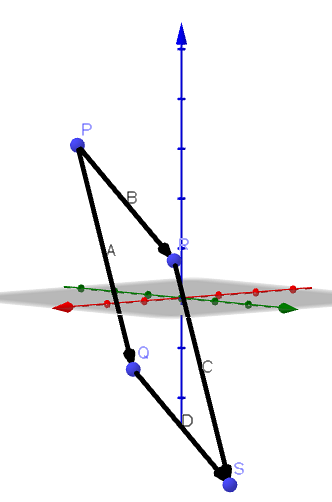
Fie A = PR și B = PQ. Apoi, unghiul format de vectorii A și B este unghiul P al triunghiului RQP, așa cum se arată în figura următoare.
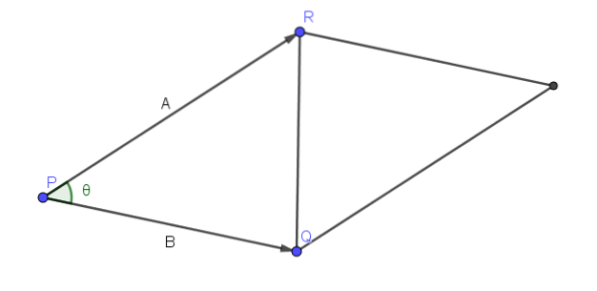
Prin urmare, aria paralelogramului care are PR și PQ ca laturi adiacente este || A |||| B || sin (ϴ), deoarece putem lua ca bază || A || iar înălțimea sa este dată de || B || sin (ϴ).
Prin aceasta, putem concluziona că || AxB || este aria paralelogramului menționat.
Exemplu
Având în vedere următoarele vârfuri ale unui patrulater P (1, -2,3), Q (4, 3, -1), R (2, 2,1) și S (5,7, -3), arătați că respectivul patrulater este un paralelogram și găsește aria acestuia.
Pentru aceasta, mai întâi determinăm vectorii care determină direcția laturilor patrulaterului. Aceasta este:
A = PQ = (1 - 4, 3 + 2, - 1 - 3) = (3, 5, - 4)
B = PR = (2 - 1, 2 + 2, 1 - 3) = (1, 4, - 2)
C = RS = (5 - 2, 7 - 2, - 3 - 1) = (3, 5, - 4)
D = QS = (5 - 4, 7 - 3, - 3 + 1) = (1, 4, - 2)
După cum putem vedea, A și C au același vector director, deci avem că ambele sunt paralele; la fel se întâmplă cu B și D. Prin urmare, concluzionăm că PQRS este un paralelogram.
Pentru a avea aria acestui paralelogram, calculăm BxA:
BxA = (i + 4j - 2k) x (3i + 5j - 4k)
= 5k + 4j - 12k - 16i - 6j + 10i
= - 6i - 2j - 7k.
Prin urmare, suprafața pătrată va fi:
|| BxA ||Două = (- 6)Două + (- Două)Două + (- 7)Două = 36 + 4 + 49 = 89.
Se poate concluziona că aria paralelogramului va fi rădăcina pătrată a lui 89.
Proprietatea 7
Doi vectori A și B sunt paraleli în R3 dacă și numai dacă AxB = 0
Demonstrație
Este clar că dacă A sau B sunt vectorul nul, se îndeplinește că AxB = 0. Deoarece vectorul zero este paralel cu orice alt vector, atunci proprietatea este validă.
Dacă niciunul dintre cei doi vectori nu este vectorul zero, avem că magnitudinile lor sunt diferite de zero; adică ambele || A || ≠ 0 ca || B || ≠ 0, deci vom avea || AxB || = 0 dacă și numai dacă sin (ϴ) = 0, iar acest lucru se întâmplă dacă și numai dacă ϴ = π sau ϴ = 0.
Prin urmare, putem concluziona AxB = 0 dacă și numai dacă ϴ = π sau ϴ = 0, ceea ce se întâmplă numai atunci când ambii vectori sunt paraleli între ei.
Proprietatea 8
Dacă A și B sunt doi vectori în R3, atunci AxB este perpendicular atât pe A cât și pe B.
Demonstrație
Pentru această dovadă, să ne amintim că doi vectori sunt perpendiculari dacă A ∙ B este egal cu zero. Mai mult, știm că:
A ∙ AxB = AxA ∙ B, dar AxA este egal cu 0. Prin urmare, avem:
A ∙ AxB = 0 ∙ B = 0.
Prin aceasta putem concluziona că A și AxB sunt perpendiculare una pe cealaltă. În mod similar, trebuie să:
AxB ∙ B = A ∙ BxB.
Deoarece BxB = 0, avem:
AxB ∙ B = A ∙ 0 = 0.
Prin urmare, AxB și B sunt perpendiculare între ele și cu aceasta proprietatea este demonstrată. Acest lucru este foarte util, deoarece ne permite să determinăm ecuația unui plan.
Exemplul 1
Obțineți o ecuație a planului care trece prin punctele P (1, 3, 2), Q (3, - 2, 2) și R (2, 1, 3).
Fie A = QR = (2 - 3,1 + 2, 3 - 2) și B = PR = (2 - 1,1 - 3, 3 - 2). Apoi A = - i + 3j + k și B = i - 2j + k. Pentru a găsi planul format din aceste trei puncte, este suficient să găsiți un vector normal pentru plan, care este AxB.
AxB = (- i + 3j + k) x (i - 2j + k) = 5i + 2j - k.
Cu acest vector și luând punctul P (1, 3, 2), putem determina ecuația planului după cum urmează:
(5, 2, - 1) ∙ (x - 1, y - 3, z - 2) = 5 (x - 1) + 2 (y - 3) - (z - 2) = 0
Astfel, avem că ecuația planului este 5x + 2y - z - 9 = 0.
Exemplul 2
Găsiți ecuația planului care conține punctul P (4, 0, - 2) și care este perpendiculară pe fiecare dintre planurile x - y + z = 0 și 2x + y - 4z - 5 = 0 .
Știind că un vector normal la un ax plan + cu + cz + d = 0 este (a, b, c), avem că (1, -1,1) este un vector normal de x - y + z = 0 y (2,1, - 4) este un vector normal de 2x + y - 4z - 5 = 0.
Prin urmare, un vector normal față de planul căutat trebuie să fie perpendicular pe (1, -1,1) și pe (2, 1, - 4). Acest vector este:
(1, -1,1) x (2,1, - 4) = 3i + 6j + 3k.
Apoi, avem că planul căutat este cel care conține punctul P (4,0, - 2) și are vectorul (3,6,3) ca vector normal.
3 (x - 4) + 6 (y - 0) + 3 (z + 2) = 0
x + 2y + z - 2 = 0.
Aplicații
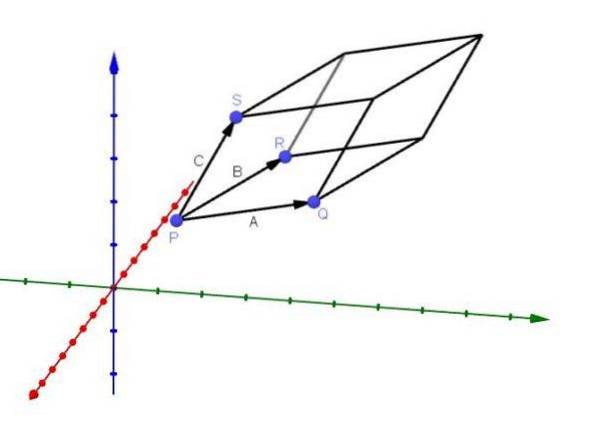
Calculul volumului unui paralelipiped
O aplicație care are produsul triplu scalar este să poată calcula volumul unui paralelipiped ale cărui margini sunt date de vectorii A, B și C, așa cum se arată în figură:
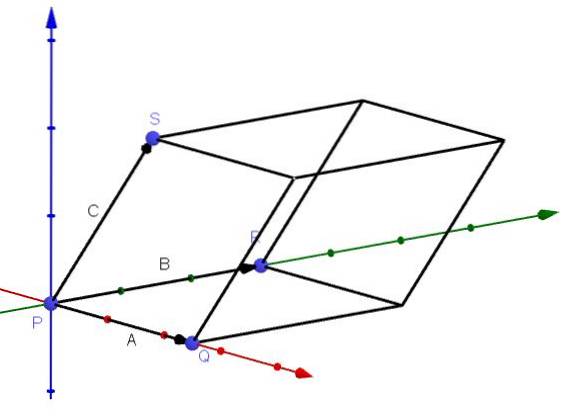
Putem deduce această aplicație în felul următor: așa cum am spus mai devreme, vectorul AxB este un vector care este normal pentru planul lui A și B. Avem, de asemenea, că vectorul - (AxB) este un alt vector normal pentru planul menționat.
Alegem vectorul normal care formează cel mai mic unghi cu vectorul C; fără pierderea generalității, să fie AxB vectorul al cărui unghi cu C este cel mai mic.
Avem că atât AxB cât și C au același punct de plecare. Mai mult, știm că aria paralelogramului care formează baza paralelipipedului este || AxB ||. Prin urmare, dacă înălțimea paralelipipedului este dată de h, avem că volumul său va fi:
V = || AxB || h.
Pe de altă parte, să luăm în considerare produsul scalar dintre AxB și C, care poate fi descris după cum urmează:
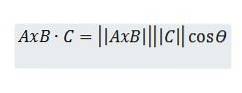
Cu toate acestea, prin proprietăți trigonometrice avem h = || C || cos (ϴ), deci avem:
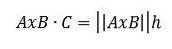
În acest fel, avem:
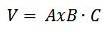
În termeni generali, avem că volumul unui paralelipiped este dat de valoarea absolută a produsului triplu scalar AxB ∙ C.
Exerciții rezolvate
Exercitiul 1
Având în vedere punctele P = (5, 4, 5), Q = (4, 10, 6), R = (1, 8, 7) și S = (2, 6, 9), aceste puncte formează un paralelipiped ale cărui margini sunt PQ, PR și PS. Determinați volumul paralelipipedului menționat.
Soluţie
Dacă luăm:
- A = PQ = (-1, 6, 1)
- B = PR = (-4, 4, 2)
- C = PS = (-3, 2, 2)
Folosind proprietatea produsului triplu scalar, avem:
AxB = (-1, 6, 1) x (-4, 4, 2) = (8, -2, 20).
AxB ∙ C = (8, -2, 20) ∙ (-3, 2, 2) = -24 -4 +80 = 52.
Prin urmare, considerăm că volumul paralelipipedului menționat este 52.
Exercițiul 2
Determinați volumul unui paralelipiped ale cărui margini sunt date de A = PQ, B = PR și C = PS, unde punctele P, Q, R și S sunt (1, 3, 4), (3, 5, 3), (2, 1, 6) și respectiv (2, 2, 5).
Soluţie
Mai întâi avem că A = (2, 2, -1), B = (1, -2, 2), C = (1, -1, 1).
Calculăm AxB = (2, 2, -1) x (1, -2, 2) = (2, -5, -6).
Apoi calculăm AxB ∙ C:
AxB ∙ C = (2, -5, -6) ∙ (1, -1, 1) = 2 + 5 - 6 = 1.
Astfel, concluzionăm că volumul paralelipipedului menționat este de 1 unitate cubică.
Referințe
- Leithold, L. (1992). Calculul cu geometrie analitică. HARLA, S.A.
- Resnick, R., Halliday, D. și Krane, K. (2001). Fizică Vol. 1. Mexic: Continental.
- Saenz, J. (s.f.). Calcul Vector 1ed. Ipotenuză.
- Spiegel, M. R. (2011). Analiza vectorială 2ed. Mc Graw Hill.
- Zill, D. G. și Wright, W. (2011). Calculul mai multor variabile 4ed. Mc Graw Hill.



Nimeni nu a comentat acest articol încă.