
Metode și exerciții de programare neliniară
programare neliniară este procesul de optimizare a unei funcții care depinde de mai multe variabile independente, care la rândul lor sunt supuse restricțiilor.
Dacă una sau mai multe dintre constrângeri sau dacă funcția de maximizare sau minimizare (numită Funcție obiectivă), nu este exprimat ca o combinație liniară a variabilelor, deci avem o problemă de programare neliniară.
Prin urmare, procedurile și metodele de programare liniară nu pot fi utilizate.
De exemplu, metoda binecunoscută nu poate fi utilizată Simplex, care se aplică numai atunci când funcția obiectivă și constrângerile sunt toate combinație liniară a variabilelor problemei.
Indice articol
- 1 Metode de programare liniară
- 1.1 Exemplu de soluție cu metodă grafică
- 2 Exerciții
- 2.1 - Exercițiul 1 (Metoda grafică)
- 2.2 - Exercițiul 2 (Metoda analitică: multiplicatori Lagrange)
- 2.3 - Exercițiul 3 (gradient nul)
- 3 Referințe
Metode de programare liniare
Pentru problemele de programare neliniară, principalele metode care trebuie utilizate sunt:
1.- Metode grafice.
2.- Multiplicatori Lagrange pentru a explora granița regiunii soluției.
3.- Calculul gradientului pentru explorarea extremelor funcției obiective.
4.- Metoda descreșterii pașilor, pentru a găsi punctele de gradient nul.
5.- Metoda modificată a multiplicatorilor Lagrange (cu condiția Karush-Kuhn-Tucker).
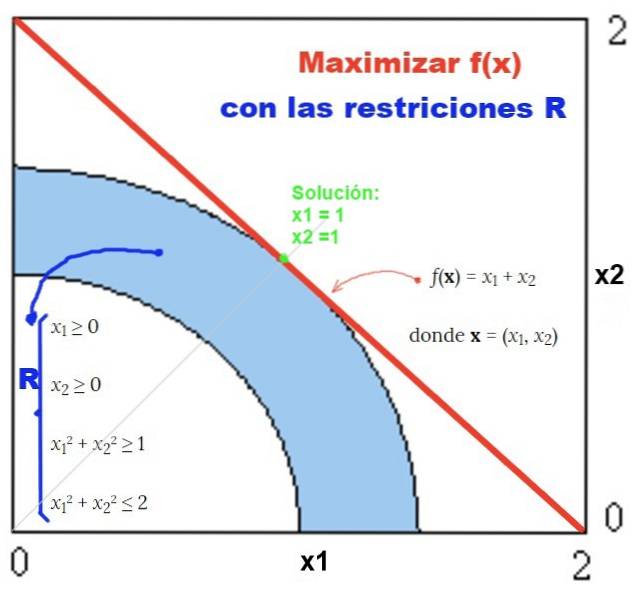
Exemplu de soluție cu metodă grafică
Un exemplu de soluție cu metoda grafică este cel care poate fi văzut în figura 2:
Instruire
- Exercițiul 1 (Metoda grafică)
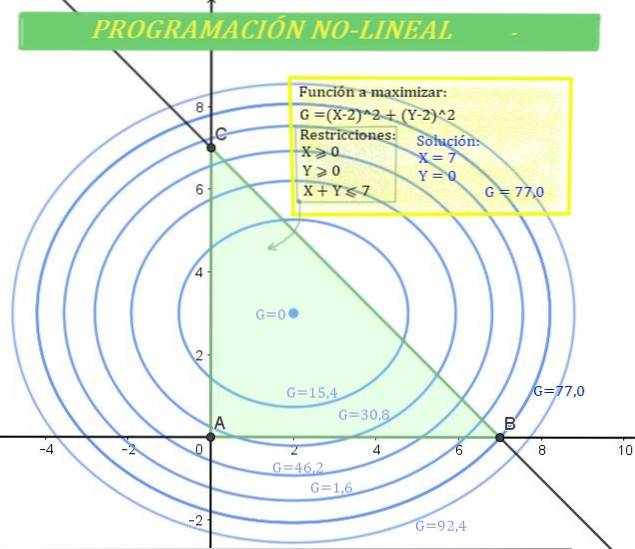
Profitul G al unei anumite companii depinde de suma vândută a produsului X și de suma vândută a produsului Y, în plus, profitul este determinat de următoarea formulă:
G = 2 (X - 2)Două + 3 (ȘI - 3)Două
Se știe că sumele X și Y au următoarele restricții:
X≥0; Y≥0 și X + Y ≤ 7
Determinați valorile lui X și Y care produc câștigul maxim.
Soluţie
În această problemă funcția obiectivă este neliniară, în timp ce inegalitățile care definesc constrângerile sunt. Este o problemă de programare neliniară.
Pentru rezolvarea acestei probleme, se va alege metoda grafică.
În primul rând, va fi determinată regiunea soluției, care este dată de constrângeri.
Ca X≥0; Y≥0, soluția trebuie găsită în primul cadran al planului XY, dar, de asemenea, trebuie să fie adevărat că X + Y ≤ 7, soluția se află în jumătatea inferioară a liniei X + Y = 7.
Regiunea soluției este intersecția primului cadran cu jumătatea inferioară a liniei, ceea ce dă naștere unei regiuni triunghiulare în care se găsește soluția. Este la fel ca în figura 1.
Pe de altă parte, câștigul G poate fi reprezentat și în plan cartezian, deoarece ecuația sa este cea a unei elipse cu centrul (2,3).
Elipsa este prezentată în figura 1 pentru diferite valori ale lui G. Cu cât este mai mare valoarea lui G, cu atât este mai mare câștigul..
Există soluții care aparțin regiunii, dar nu dau valoarea maximă a G, în timp ce altele, cum ar fi G = 92,4, se află în afara zonei verzi, adică a zonei de soluție.
Apoi, valoarea maximă a lui G, astfel încât X și Y să aparțină regiunii soluției, corespunde:
G = 77 (câștig maxim), care este dat pentru X = 7 și Y = 0.
Interesant, profitul maxim apare atunci când valoarea vânzărilor produsului Y este zero, în timp ce cantitatea produsului X atinge cea mai mare valoare posibilă..
- Exercițiul 2 (Metoda analitică: multiplicatori Lagrange)
Găsiți soluția (x, y) care face funcția f (x, y) = xDouă + 2 șiDouă să fie maxim în regiunea g (x, y) = xDouă + DaDouă - 1 = 0.
Soluţie
Este în mod clar o problemă de programare neliniară, deoarece atât funcția obiectivă f (x, y), cât și restricția g (x, y) = 0, nu sunt o combinație liniară a variabilelor x și y.
Se va folosi metoda multiplicatorilor Lagrange, care necesită mai întâi definirea funcției Lagrange L (x, y, λ):
L (x, y, λ) = f (x, y) - λ g (x, y) = xDouă + 2 șiDouă - λ (xDouă + DaDouă - 1)
Unde λ este un parametru numit Multiplicator Lagrange.
Pentru a determina valorile extreme ale funcției obiective f, în regiunea soluției dată de restricția g (x, y) = 0, urmați acești pași:
-Găsiți derivatele parțiale ale funcției Lagrange L, în raport cu x, y, λ.
-Setați fiecare derivată la zero.
Iată secvența acestor operații:
- ∂L / ∂x = 2x - 2λx = 0
- ∂L / ∂y = 4y - 2λy = 0
- ∂L / ∂λ = - (xDouă + DaDouă - 1) = 0
Soluții de sistem posibile
O posibilă soluție a acestui sistem este λ = 1 astfel încât prima ecuație să fie satisfăcută, caz în care y = 0 astfel încât a doua să fie satisfăcută.
Această soluție implică faptul că x = 1 sau x = -1 pentru a treia ecuație care trebuie îndeplinită. În acest fel, s-au obținut două soluții S1 și S2:
S1: (x = 1, y = 0)
S2: (x = -1, y = 0).
Cealaltă alternativă este că λ = 2 astfel încât a doua ecuație să fie satisfăcută, indiferent de valoarea y.
În acest caz, singura modalitate de îndeplinire a primei ecuații este că x = 0. Având în vedere a treia ecuație, există doar două soluții posibile, pe care le vom numi S3 și S4:
S3: (x = 0, y = 1)
S4: (x = 0, y = -1)
Pentru a afla care sau care dintre aceste soluții maximizează funcția obiectivă, continuăm să înlocuim cu f (x, y):
S1: f (1, 0) = 1Două + 2.0Două = 1
S2: f (-1, 0) = (-1)Două + 2.0Două = 1
S3: f (0, 1) = 0Două + 2.1Două = 2
S4: f (0, -1) = 0Două + douăzeci și unu)Două = 2
Concluzionăm că soluțiile care maximizează f, când x și y aparțin circumferinței g (x, y) = 0 sunt S3 și S4.
Perechile de valori (x = 0, y = 1) și (x = 0, y = -1) maximizează f (x, y) în regiunea soluției g (x, y) = 0.
- Exercițiul 3 (gradient nul)
Găsiți soluții (x, y) pentru funcția obiectivă:
f (x, y) = xDouă + 2 șiDouă
Fie maxim în regiunea g (x, y) = xDouă + DaDouă - 1 ≤ 0.
Soluţie
Acest exercițiu este similar cu exercițiul 2, dar regiunea soluției (sau restricției) se extinde la regiunea interioară a circumferinței g (x, y) = 0, adică la cercul g (x, y) ≤ 0. Aceasta include la circumferință și regiunea sa interioară.
Soluția la frontieră a fost deja stabilită în exercițiul 2, dar regiunea interioară rămâne de explorat.
Pentru a face acest lucru, gradientul funcției f (x, y) trebuie calculat și setat egal cu zero, pentru a găsi valori extreme în regiunea soluției. Acest lucru este echivalent cu calcularea derivatelor parțiale ale lui f față de x și respectiv y și setarea egală cu zero:
∂f / ∂x = 2 x = 0
∂f / ∂y = 4 y = 0
Acest sistem de ecuații are ca singură soluție (x = 0, y = 0) care aparține cercului g (x, y) ≤ 0.
Înlocuind această valoare în funcția f rezultă:
f (0, 0) = 0
În concluzie, valoarea maximă pe care o ia funcția în regiunea soluției este 2 și apare la limita regiunii soluției, pentru valorile (x = 0, y = 1) și (x = 0, y = -1 ).
Referințe
- Avriel, M. 2003. Programare neliniară. Editura Dover.
- Bazaraa. 1979. Programare neliniară. John Wiley & Sons.
- Bertsekas, D. 1999. Programare neliniară: ediția a II-a. Athena Scientific.
- Nocedal, J. 1999. Optimizare numerică. Springer-Verlag.
- Wikipedia. Programare neliniară. Recuperat de pe: es.wikipedia.com



Nimeni nu a comentat acest articol încă.