reactanța capacitivă este rezistența pe care un condensator, un element de reglare a debitului de sarcină într-un circuit de curent alternativ, se opune trecerii curentului.
Într-un circuit format dintr-un condensator și activat de o sursă de curent alternativ, reactanța capacitivă X poate fi definităC după cum urmează:
XC = 1 / ωC
Sau, de asemenea:
XC = 1 / 2πfC
Unde C este capacitatea condensatorului și ω este frecvența unghiulară a sursei, legată de frecvența f de:
ω = 2πf
Reactanța capacitivă depinde de inversul frecvenței, de aceea la frecvențe înalte tinde să fie mică, în timp ce la frecvențe joase, reactanța este mare.
Unitatea sistemului internațional pentru măsurarea reactanței capacitive este ohmul (Ω), cu condiția ca capacitatea C a condensatorului să fie în farad (prescurtat F) și frecvența să fie exprimată în secunde inverse (s-1).
În timp ce sarcina durează, o tensiune alternativă și un curent sunt stabilite prin condensator, ale cărui amplitudini sau valori maxime, notate respectiv ca VC și euC, sunt legate de reactanța capacitivă în mod analog legii lui Ohm:
VC = EuC ⋅ XC
Într-un condensator, tensiunea este cu 90 ° în spatele curentului sau curentul este cu 90 ° înaintea curentului, după cum preferați. În orice caz, frecvența este aceeași.
Când XC este foarte mare, curentul tinde să fie mic și făcând ca valoarea lui X să tindă la infinitC, condensatorul se comportă ca un circuit deschis și curentul este zero.
Indice articol
Să vedem un exemplu de calcul al reactanței capacitive: să presupunem că un condensator de 6 μF este conectat la o ieșire de curent alternativ de 40 V și frecvență F 60 Hz.
Pentru a găsi reactanța capacitivă se folosește definiția dată la început. Frecvența unghiulară ω este dată de:
ω = 2πf = 2π x 60 Hz = 377 s-1
Apoi, acest rezultat este substituit în definiție:
XC = 1 / ωC = 1 / (377 s-1x 6 x10 -6 F) = 442,1 ohm
Acum să vedem amplitudinea curentului care curge în circuit. Deoarece sursa oferă o tensiune de amplitudine VC = 40 V, folosim relația dintre reactanța capacitivă, curent și tensiune pentru a calcula amplitudinea curentului sau curentului maxim:
EuC = VC / XC = 40 V / 442,1 ohm = 0,09047 A = 90,5 m A.
Dacă frecvența devine foarte mare, reactanța capacitivă devine mică, dar dacă frecvența devine 0 și am avea un curent continuu, reactanța ar tinde să fie infinită..
Când un condensator este conectat la o sursă de curent alternativ, pe măsură ce oscilează și își schimbă polaritatea, condensatorul experimentează sarcini și descărcări alternative..
Pentru o frecvență de 60 Hz ca cea din exemplu, tensiunea este pozitivă de 60 de ori pe secundă și negativă de încă 60 de ori pe secundă.
Creșterea tensiunii împinge curentul într-o direcție, dar dacă condensatorul se descarcă, curentul este produs în direcția opusă care se opune primului..
Dacă vC (t) = Vm sin ωt, știind că capacitatea este raportul dintre sarcină și tensiune, vom avea sarcina:
C = q / V → q (t) = CV = CVm sen ωt
Și având sarcina în funcție de timp, vom avea curentul, care este derivatul aceleia:
euC(t) = CVm ω cos ωt
Dar sinusul și cosinusul sunt legate de: cos α = sin (α + π / 2), prin urmare:
euC(t) = CVm ω sin (ωt + π / 2) = IC păcat (ωt + π / 2)
Cu IC = CVC ω
După cum puteți vedea, există o diferență de 90 ° de avans al curentului față de tensiune, așa cum a fost comentat la început.
În descrierea acestui tip de circuite, conceptul de fazor, care este foarte asemănător cu un vector și permite orice cantitate alternativă precum curent, tensiune sau impedanță să fie reprezentată în planul complex.
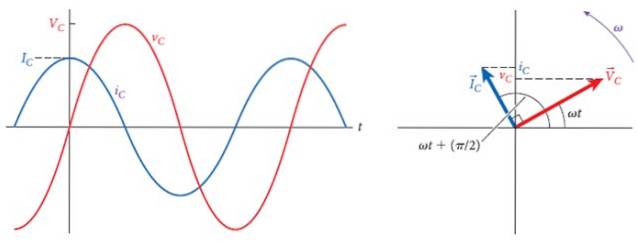
Următoarea figură arată, în dreapta, fazorii de tensiune și curent din condensator, care formează un unghi de 90 ° între ei, care este diferența de fază dintre cei doi..
În stânga sunt graficele respective, de amplitudini diferite, dar aceeași frecvență. În timp, curentul conduce tensiunea și atunci când este maximă, curentul este zero și când tensiunea este zero, curentul este maxim, dar cu polaritatea inversată.
Într-un circuit cu rezistențe, condensatori și inductanțe, reactanța este partea imaginară a impedanței Z, o cantitate complexă care în circuitele de curent alternativ are un rol similar cu cel al rezistenței electrice pentru circuitele de curent continuu..
De fapt, impedanța unui circuit este definită ca raportul dintre tensiune și curent:
Z = V / I
Pentru un condensator sau condensator, impedanța acestuia este dată de coeficientul:
ZC = v (t) / i (t) = VC sin sint / IC păcat (ωt + π / 2)
O modalitate de a exprima tensiunea și curentul ca fazori este indicând amplitudinea și unghiul de fază (formă polară):
v (t) = VC ∠ 0º
i (t) = IC ∠ 90º
Prin urmare:
ZC = VC ∠ 0º / IC ∠ 90º = (VC / EuC) ∠ 0º -90º =
= VC / CVC ω ∠ -90º = (1 / ωC) ∠ -90º =
ZC = (- j) XC
Adică, impedanța condensatorului este reactanța sa capacitivă înmulțită cu negativul unității imaginare.
Impedanța unui circuit de curent alternativ cu rezistențe, condensatori și inductori poate fi, de asemenea, reprezentată binomial prin:
Z = R + jX
În această ecuație, R reprezintă rezistența, care corespunde părții reale, j este unitatea imaginară și X este reactanța, care poate fi capacitivă sau inductivă sau o combinație a ambelor, dacă aceste elemente sunt prezente în același timp în circuit.
Dacă circuitul conține un rezistor și un condensator în serie, impedanța lor este:
Z = ZR + ZC
Deoarece în rezistență tensiunea și curentul sunt în fază, impedanța rezistivă este pur și simplu valoarea rezistenței R.
În cazul impedanței capacitive, am văzut deja că ZC = -jXC , prin urmare, impedanța circuitului RC este:
Z = R - jXC = R - j (1 / ωC)
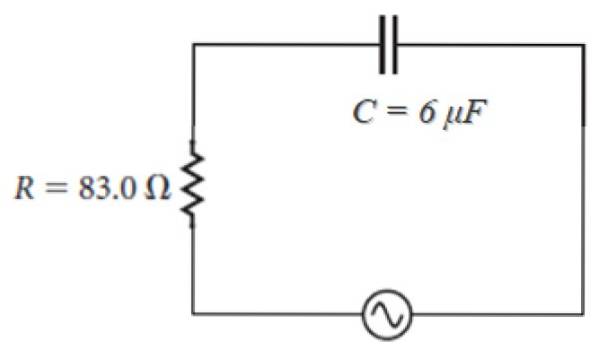
De exemplu, în circuitul prezentat mai jos, a cărui sursă este de forma:
100 V ⋅ sin (120πt)
Observând că ω = 120π, impedanța este:
Z = 83,0 - j [(1 / (120π ⋅ 6 x 10-6)] ohm = 83,0 - 442,1 j ohm.
Filtrele de trecere înaltă, filtrele de trecere joasă, circuitele de tip punte pentru măsurarea capacităților și inductanțelor și circuitele de schimbare de fază sunt printre principalele aplicații ale circuitelor care conțin reactanțe capacitive, în combinație cu inductanțe și rezistențe electrice..
În stereo, unele difuzoare vin cu difuzoare separate. woofer (mai mare) pentru frecvențe joase și tweeter sau claxon mic pentru frecvențe înalte. Acest lucru îmbunătățește performanța și calitatea audio.
Folosesc condensatori care împiedică sosirea frecvențelor joase în tweeter, în timp ce în woofer se adaugă un inductor pentru a evita semnalele de înaltă frecvență, deoarece inductanța are o reactanță proporțională cu frecvența: XL = 2πfL.
Nimeni nu a comentat acest articol încă.