relație matematică este legătura care există între elementele unui subset față de produsul a două seturi. A funcţie implică operația matematică pentru a determina valoarea unei variabile dependente pe baza valorii unei variabile independente. Fiecare funcție este o relație, dar nu orice relație este o funcție.
| Relaţie | Funcţie | |
|---|---|---|
| Definiție | Subset de perechi ordonate care corespund produsului cartezian din două seturi. | Operație matematică care trebuie efectuată cu variabila X pentru a obține variabila Da. |
| Notaţie | X R Da; X este legat de Da. | Da= ƒ (X); Da este o funcție a X. |
| Caracteristici |
|
|
| Exemple |
|
|
Se numește relația binară a unei mulțimi A într-o mulțime B sau relația dintre elementele lui A și B la fiecare subset C al produsului cartezian A x B.
Adică, dacă mulțimea A este alcătuită din elementele 1, 2 și 3, iar mulțimea B este alcătuită din elementele 4 și 5, produsul cartezian al lui A x B va fi perechile ordonate:
A x B = (1,4), (2,4), (3, 4), (1,5), (2,5), (3,5).
Subsetul C = (2,4), (3,5) va fi o relație a lui A și B deoarece este compus din perechile ordonate (2,4) și (3, 5), rezultatul cartezianului produs din A x B.
„Fie A și B orice două seturi ne-goale, fie A x B setul de produse al ambelor, adică: A x B este format din perechile ordonate (x, y) astfel încât X este elementul lui A și Da este pentru B. Dacă orice subset C este definit în A x B, o relație binară în A și B se determină automat după cum urmează:
X R Da dacă și numai dacă (x, y) ∈ C
(notația X R Da Mijloace "X este legat de Da").
Vom numi setul A set de pornire și vom numi setul B set de sosire.
domeniul relației sunt elementele care alcătuiesc setul de pornire, în timp ce intervalul raportului sunt elementele setului de sosire.
A stabilit LA din X elemente ale bărbaților dintr-o populație și B este ansamblul Da elemente ale femeilor din aceeași populație. O relație este stabilită atunci când „X este căsătorit cu Da".
Când vorbim despre o funcție matematică a unei mulțimi A într-o mulțime B ne referim la o regulă sau mecanism care leagă elementele mulțimii A cu un element al mulțimii B.
„Sean X Da Da două variabile reale, se spune apoi că y este o funcție a lui x da pentru fiecare valoare pe care o iau X corespunde unei valori de Da."
Variabila independentă este X in timp ce Da este variabila sau funcția dependentă:
y = ƒ (x)
Setul în care X se numeste domeniul funcției (original) și variația lui Da gama de funcții (imagine).
Setul de perechi (X, Da) astfel încât Da= ƒ (X) se numește grafic funcțional; dacă sunt reprezentate în axe carteziene, se obține o familie de puncte numită grafic funcțional.
În matematică obținem multe exemple de funcții. Iată exemple de funcții emblematice.
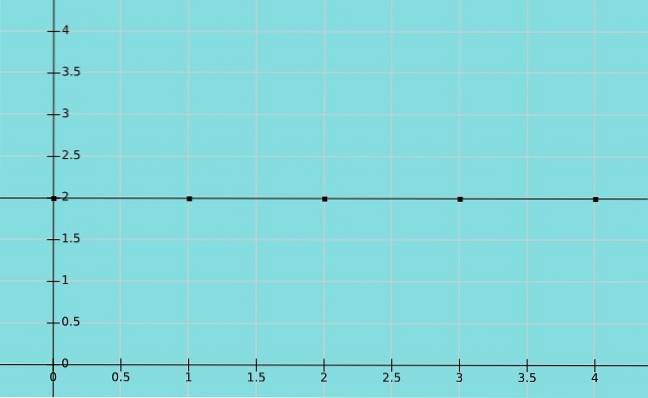
O funcție se numește constantă dacă elementul mulțimii B care corespunde mulțimii A este același. În acest caz, toate valorile lui x corespund aceleiași valori a lui y. Astfel, domeniul este numărul real, în timp ce domeniul este o valoare constantă.
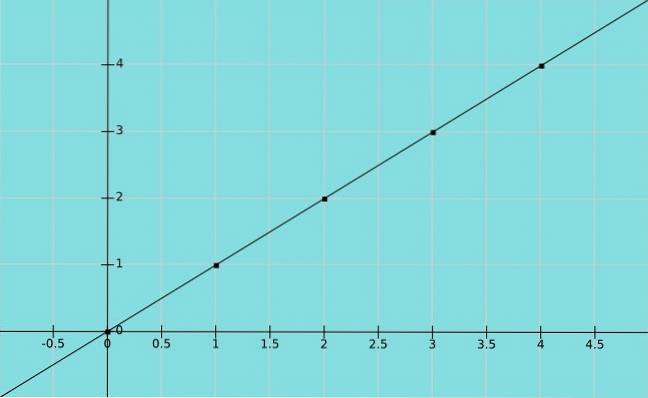
Să presupunem X este o variabilă și asta Da ia aceeași valoare ca X. Avem apoi o funcție de identitate y = x, unde perechileX y) în grafic sunt (1,1), (2,2), (3,3) și așa mai departe.
O funcție polinomială îndeplinește forma y = anXn+lan-1+Xn-1+… + ADouăXDouă+la1x + a0. Graficul de mai sus arată funcția ƒ (x) = xDouă+x-2.
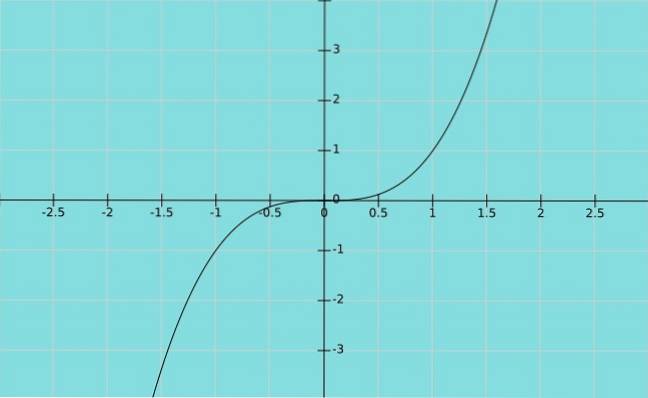
Acum presupunem că variabila dependentă Da este egală cu variabila independentă X ridicat la cub. Avem funcția y = x3, al cărui grafic este prezentat mai jos:
Nimeni nu a comentat acest articol încă.