
Proprietăți de simetrie axială, exemple și exerciții
simetrie axială Apare atunci când punctele unei figuri coincid cu punctele unei alte figuri prin intermediul unei bisectoare drepte numite axa de simetrie. Se mai numește simetrie radială, rotațională sau cilindrică..
Se aplică de obicei în figuri geometrice, dar este ușor de observat în natură, deoarece există animale precum fluturi, scorpioni, buburuze sau oameni care prezintă simetrie axială..

Indice articol
- 1 Cum se găsește simetricul axial
- 2 Proprietăți ale simetriei axiale
- 3 Exemple de simetrie axială
- 4 exerciții de simetrie axială
- 4.1 Exercițiul 1
- 4.2 Exercițiul 2
- 4.3 Exercițiul 3
- 4.4 Exercițiul 4
- 5 Referințe
Cum se găsește axial simetric
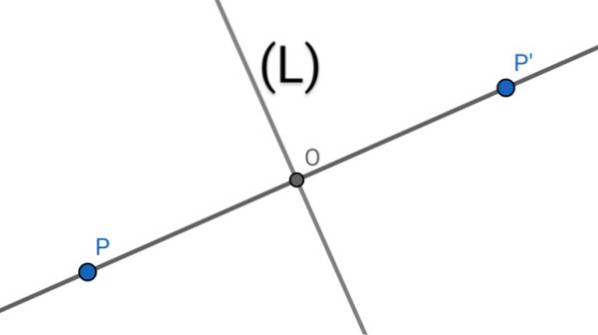
Pentru a găsi simetria axială P 'a unui punct P în raport cu o linie (L), se efectuează următoarele operații geometrice:
1.- Se trasează perpendicular pe linia (L) care trece prin punctul P.
2.- Interceptarea celor două linii determină un punct O.
3.- Se măsoară lungimea segmentului PO, apoi această lungime este copiată peste linia (PO) începând de la O în direcția de la P la O determinând punctul P '.
4.- Punctul P 'este simetricul axial al punctului P în raport cu axa (L), deoarece linia (L) este mediatrizarea segmentului PP', unde O este punctul de mijloc al segmentului menționat.
Proprietățile simetriei axiale
- Simetria axială este izometrică, adică se păstrează distanțele unei figuri geometrice și simetria corespunzătoare a acesteia.
- Măsura unui unghi și cea a simetricului său sunt egale.
- Simetria axială a unui punct de pe axa de simetrie este punctul în sine.
- Linia simetrică a unei linii paralele cu axa de simetrie este, de asemenea, o linie paralelă cu axa menționată.
- O linie secantă către axa de simetrie are ca linie simetrică o altă linie secantă care, la rândul ei, intersectează axa de simetrie în același punct al liniei originale.
- Imaginea simetrică a unei linii este o altă linie care formează un unghi cu axa de simetrie de aceeași măsură ca cea a liniei originale.
- Imaginea simetrică a unei linii perpendiculare pe axa de simetrie este o altă linie care se suprapune pe prima.
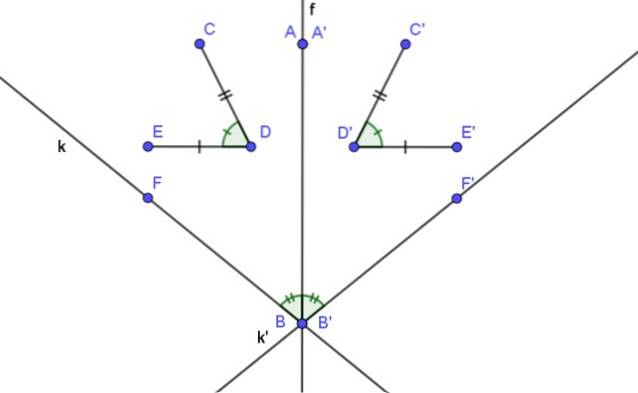
- O linie și linia ei simetrică axială formează un unghi a cărui bisectoare este axa de simetrie.
Exemple de simetrie axială
Natura prezintă exemple abundente de simetrie axială. De exemplu, puteți vedea simetria fețelor, insectelor precum fluturii, reflexia pe suprafețele și oglinzile apei calme sau frunzele plantelor, printre multe altele..


Exerciții de simetrie axială
Exercitiul 1
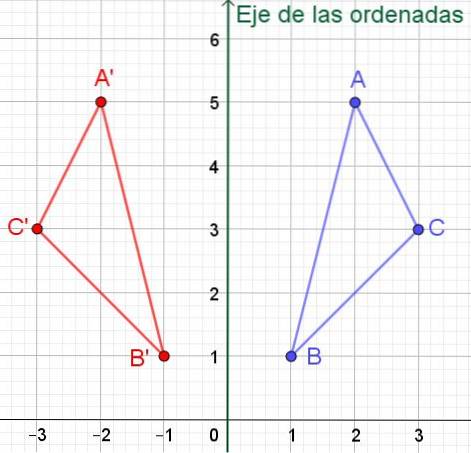
Avem triunghiul vârfurilor A, B și C ale căror coordonate carteziene sunt respectiv A = (2, 5), B = (1, 1) și C = (3,3). Găsiți coordonatele carteziene ale triunghiului simetric în jurul axei Y (axa ordonată).
Soluţie: Dacă un punct P are coordonate (x, y) atunci simetricul său față de axa ordonată (axa Y) este P '= (- x, y). Adică, valoarea abscisei sale schimbă semnul, în timp ce valoarea ordonatei rămâne aceeași.
În acest caz, triunghiul simetric cu vârfurile A ', B' și C 'va avea coordonate:
A '= (- 2, 5); B '= (- 1, 1) și C' = (- 3, 3) așa cum se poate vedea în figura 6.
Exercițiul 2
Cu referire la triunghiul ABC și A'B'C 'lui simetric din exercițiul 1, verificați dacă laturile corespunzătoare ale triunghiului original și simetricul său au aceeași lungime.
Soluţie: Pentru a găsi distanța sau lungimea laturilor folosim formula distanței euclidiene:
d (A, B) = √ ((Bx - Ax) ^ 2 + (By - Ay) ^ 2) = √ ((1-2) ^ 2 + (1-5) ^ 2) = √ ((- 1 ) ^ 2 + (-4) ^ 2) = √ (17) = 4.123
Lungimea laturii simetrice corespunzătoare A'B 'este calculată mai jos:
d (A ', B') = √ ((Bx'-Ax ') ^ 2 + (By'-Ay') ^ 2) = √ ((- 1 + 2) ^ 2 + (1-5) ^ 2 ) = √ ((1) ^ 2 + (-4) ^ 2) = √ (17) = 4.123
În acest fel, se verifică faptul că simetria axială păstrează distanța dintre două puncte. Procedura poate fi repetată pentru celelalte două laturi ale triunghiului și simetric pentru verificarea invarianței în lungime. De exemplu | AC | = | A'C '| = √5 = 2.236.
Exercițiul 3
În raport cu triunghiul ABC și simetricul său A'B'C 'din exercițiul 1, verificați dacă unghiurile corespunzătoare ale triunghiului original și simetricul său au aceeași măsură unghiulară.
Soluţie: Pentru a determina măsurile unghiurilor BAC și B'A'C ', se va calcula mai întâi produsul scalar al vectorilor AB cu AC și apoi produsul punct al A'B ' cu A'C '.
Amintindu-mi că:
A = (2, 5), B = (1, 1) și C = (3,3)
A '= (- 2, 5); B '= (- 1, 1) și C' = (- 3, 3).
Are:
AB = <1-2, 1-5> Da AC = <3-2, 3-5>
în mod similar
A'B ' = <-1+2, 1-5> Da AC = <-3+2, 3-5>
Apoi se găsesc următoarele produse scalare:
AB⋅AC = <-1, -4>⋅<1, -2> = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7
În mod similar
A'B'⋅A'C ' = <1, -4>⋅<-1, -2> = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7
Măsura unghiului BAC este:
∡BAC = ArcCos ( AB⋅AC / (| |AB |⋅ |AC |)) =
ArcCos (7 / (4.123⋅2.236)) = 40.6º
În mod similar, măsura unghiului B'A'C 'este:
∡B'A'C '= ArcCos ( A'B'⋅A'C ' / (| |A'B '|⋅ |A'C | |)) =
ArcCos (7 / (4.123⋅2.236)) = 40.6º
Concluzionând că simetria axială păstrează măsurarea unghiului.
Exercițiul 4
Fie un punct P al coordonatelor (a, b). Găsiți coordonatele simetriei sale axiale P 'față de dreapta y = x.
Soluţie: Vom numi (a ', b') coordonatele punctului simetric P 'față de linia y = x. Punctul de mijloc M al segmentului PP 'are coordonate ((a + a') / 2, (b + b ') / 2) și este, de asemenea, pe linia y = x, deci este adevărată următoarea egalitate:
a + a '= b + b'
Pe de altă parte, segmentul PP 'are panta -1, deoarece este perpendicular pe linia y = x cu panta 1, deci se menține următoarea egalitate:
b - b '= a' -a
Rezolvând pentru cele două egalități anterioare a 'și b' se concluzionează că:
a '= b și că b' = a.
Adică, având în vedere un punct P (a, b), simetria sa axială în raport cu linia y = x este P '(b, a).
Referințe
- Arce M., Blázquez S și alții. Transformări ale planului. Recuperat de la: educutmxli.files.wordpress.com
- Calcul cc. Simetrie axială. Recuperat de la: calculo.cc
- Superprof. Simetrie axială. Recuperat de pe: superprof.es
- wikipedia. Simetrie axială. Recuperat de pe: es.wikipedia.com
- wikipedia. Simetrie circulară. Recuperat de pe: en.wikipedia.com



Nimeni nu a comentat acest articol încă.