
Suma de polinoame, cum se face, exemple, exerciții
suma polinoamelor este operația care constă în adăugarea a două sau mai multe polinoame, rezultând un alt polinom. Pentru a-l realiza, este necesar să adăugați termenii de aceeași ordine pentru fiecare dintre polinoame și să indicați suma rezultată.
Să analizăm mai întâi pe scurt semnificația „termenilor de aceeași ordine”. Orice polinom este alcătuit din adunări și / sau scăderi de termeni.

Termenii pot fi produse de numere reale și una sau mai multe variabile, reprezentate prin litere, de exemplu: 3xDouă și -√5.aDouăbc3 sunt termeni.
Ei bine, termenii de aceeași ordine sunt cei care au același exponent sau putere, deși pot avea un coeficient diferit.
-Termenii de ordine egali sunt: 5x3, √2 x3 și -1 / 2x3
-Termeni de ordine diferiți: -2x-Două, 2xy-1 și √6xDouăDa
Este important să rețineți că numai termenii de aceeași ordine pot fi adăugați sau scădați, operație cunoscută sub numele de reducere. În caz contrar, suma este lăsată pur și simplu indicată.
Odată ce conceptul de termeni de aceeași ordine a fost clarificat, polinoamele sunt adăugate urmând acești pași:
-Ordin Mai întâi polinoamele care trebuie adăugate, toate în același mod, fie într-un mod crescător, fie descrescător, adică cu puterile de la inferior la superior sau invers.
-A termina, în cazul în care orice putere lipsește în secvență.
-Reduce ca termeni.
-Indica suma rezultată.
Indice articol
- 1 Exemple de adăugare de polinoame
- 1.1 Adăugați două sau mai multe polinoame cu mai multe variabile
- 2 Exerciții pentru adăugarea de polinoame
- 2.1 - Exercițiul 1
- 2.2 - Exercițiul 2
- 3 Referințe
Exemple de adăugare de polinoame
Vom începe prin adăugarea a două polinoame cu o singură variabilă numită X, de exemplu polinoamele P (x) și Q (x) date de:
P (x) = 2xDouă - 5x4 + 2x -x5 - 3x3 +12
Q (x) = x5- 25 x + xDouă
Urmând pașii descriși, începeți prin a le ordona în ordine descrescătoare, care este cel mai obișnuit mod:
P (x) = -x5- 5x4 - 3x3 + 2xDouă + 2x +12
Q (x) = x5+ XDouă - 25x
Polinomul Q (x) nu este complet, se vede că lipsesc puterile cu exponenții 4, 3 și 0. Acesta din urmă este pur și simplu termenul independent, cel care nu are literă.
Q (x) = x5+ 0x4 + 0x3 + XDouă - 25x + 0
Odată ce acest pas este făcut, acestea sunt gata de adăugat. Puteți adăuga termenii asemănători și apoi indica suma sau puteți plasa polinoamele ordonate unul sub celălalt și reduceți prin coloane, în acest fel:
- X5 - 5x4 - 3x3 + 2xDouă + 2x +12
+ X5 + 0x4 + 0x3 + XDouă - 25x + 0 +
--
0x5-5x4 - 3x3 +3xDouă - 23x + 12 = P (x) + Q (x)
Este important să rețineți că, atunci când este adăugat, se face respectând algebraic regula semnelor, în acest mod 2x + (-25 x) = -23x. Adică, dacă coeficienții au un semn diferit, se scad și rezultatul poartă semnul celui mai mare.
Adăugați două sau mai multe polinoame cu mai multe variabile
Când vine vorba de polinoame cu mai multe variabile, una dintre ele este aleasă pentru a o comanda. De exemplu, să presupunem că cereți să adăugați:
R (x, y) = 5xDouă - 4yDouă + 8xy - 6y3
Y:
T (x, y) = ½ xDouă- 6yDouă - 11xy + x3Da
Se alege una dintre variabile, de exemplu x pentru a comanda:
R (x, y) = 5xDouă + 8xy - 6y3 - 4yDouă
T (x, y) = + x3y + ½ xDouă - 11xy - 6yDouă
Imediat se completează termenii lipsă, conform cărora fiecare polinom are:
R (x, y) = 0x3y + 5xDouă + 8xy - 6y3 - 4yDouă
T (x, y) = + x3y + ½ xDouă - 11xy + 0y3 - 6yDouă
Și amândoi sunteți gata să reduceți termeni similari:
0x3y + 5xDouă + 8xy - 6y3 - 4yDouă
+ X3y + ½ xDouă - 11xy + 0y3 - 6yDouă +
-
+ X3și + 11 / 2xDouă - 3xy - 6y3 - 10yDouă = R (x, y) + T (x, y)
Exerciții de adăugare polinomială
- Exercitiul 1
În următoarea sumă de polinoame, indicați termenul care trebuie să meargă în spațiul gol pentru a obține suma polinomială:
-5x4 + 0x3 + 2xDouă + 1
X5 + 2x4 - 21xDouă + 8x - 3
2x5 +9x3 -14x
-
-6x5+10x4 -0x3 + 5xDouă - 11x + 21
Soluţie
Pentru a obține -6x5 este necesar un termen al formei ax5, astfel încât:
a + 1+ 2 = -6
Prin urmare:
a = -6-1-2 = -9
Și termenul de căutare este:
-9x5
-Procedați într-un mod similar pentru a găsi restul termenilor. Iată cel pentru exponentul 4:
-5 + 2 + a = 10 → a = 10 + 5-2 = 13
Termenul lipsă este: 13x4.
-Pentru puterile lui x3 este imediat că termenul trebuie să fie -9x3, astfel coeficientul termenului cub este 0.
-În ceea ce privește puterile pătrate: a + 8 - 14 = -11 → a = -11 - 8 + 14 = -5 și termenul este -5xDouă.
-Termenul liniar se obține cu ajutorul unui +8 -14 = -11 → a = -11 + 14 - 8 = -5, termenul lipsă fiind -5x.
-În cele din urmă, termenul independent este: 1 -3 + a = -21 → a = -19.
- Exercițiul 2
Un teren plat este îngrădit așa cum se arată în figură. Găsiți o expresie pentru:
a) Perimetrul și
b) Aria sa, în ceea ce privește lungimile indicate:
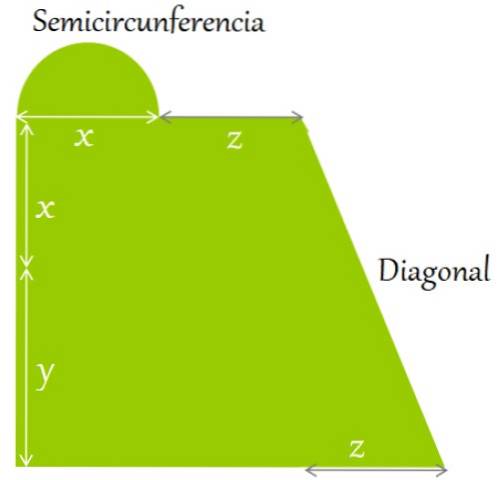
Solutie la
Perimetrul este definit ca suma laturilor și contururilor figurii. Începând din colțul din stânga jos, în sensul acelor de ceasornic, avem:
Perimetru = y + x + lungimea semicercului + z + lungimea diagonalei + z + z + x
Semicercul are un diametru egal cu x. Deoarece raza este jumătate din diametru, trebuie să:
Raza = x / 2.
Formula pentru lungimea unei circumferințe complete este:
L = 2π x Raza
Atunci:
Lungimea semicercului = ½. 2π (x / 2) = πx / 2
La rândul său, diagonala este calculată cu teorema lui Pitagora aplicată pe laturi: (x + y) care este partea verticală și z, care este orizontală:
Diagonal = [(x + y)Două + zDouă]1/2
Aceste expresii sunt substituite în cea a perimetrului, pentru a obține:
Perimetru = y + x + πx / 2 + z + [(x + y)Două + zDouă]1/2+ z + x + z
Termenii similari sunt reduși, deoarece adăugarea necesită simplificarea cât mai mult posibil a rezultatului:
Perimetru = y + [x + π (x / 2) + x] + z + z + z + [(x + y)Două + zDouă]1/2 = y + (2 + π / 2) x + 3z
Soluția b
Aria rezultată este suma ariei dreptunghiului, a semicercului și a triunghiului dreptunghiular. Formulele pentru aceste domenii sunt:
-Dreptunghi: baza x inaltime
-Semicerc: ½ π (Raza)Două
-Triunghi: baza x inaltime / 2
Zona dreptunghiului
(x + y). (x + z) = xDouă + xz + yx + yz
Zona semicercului
½ π (x / 2)Două = π xDouă / 8
Zona triunghiului
½ z (x + y) = ½ zx + ½ zy
Suprafata totala
Pentru a găsi aria totală, se adaugă expresiile găsite pentru fiecare zonă parțială:
Suprafața totală = xDouă + xz + yx + yz + (π xDouă / 8) + ½ zx + ½ zy
Și, în cele din urmă, toți termenii similari sunt reduși:
Suprafața totală = (1 + π / 8) xDouă + 3/2 xy + 3 / 2yz + yx
Referințe
- Baldor, A. 1991. Algebra. Editorial Cultural Venezolana S.A.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematica este distractivă. Adunarea și scăderea polinoamelor. Recuperat de pe: mathsisfun.com.
- Institutul Monterey. Adunarea și scăderea polinoamelor. Recuperat de pe: montereyinstitute.org.
- UC Berkeley. Algebra polinoamelor. Recuperat de la: math.berkeley.edu.



Nimeni nu a comentat acest articol încă.