
Sumare telescopică cum se rezolvă și cum se rezolvă exercițiile

însumare telescopic este o ramură a operațiilor cu serii numerice. Abordează însumarea elementelor de la o valoare inițială la „n” a expresiilor al căror argument respectă oricare dintre următoarele tipare:
(FX - Fx + 1); (Fx + 1 - FX)
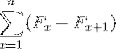
De asemenea:
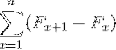

Ele reprezintă o însumare de elemente care, atunci când sunt dezvoltate, sunt supuse anulării unor termeni opuși. Permitând definirea următoarei egalități pentru însumările telescopice:
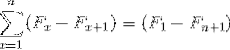
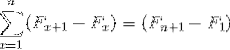
Numele său provine din relația cu apariția unui telescop clasic, care ar putea fi pliat și desfășurat, schimbându-și în special dimensiunea. În același mod, sumările telescopice, care sunt de natură infinită, pot fi rezumate în expresia simplificată:
F1 - Fn + 1
Indice articol
- 1 Demo
- 2 Cum se rezolvă?
- 2.1 Descompunerea în fracții simple
- 3 Istorie
- 4 Exerciții
- 4.1 Exercițiul 1
- 4.2 Exercițiul 2
- 5 Referințe
Demonstrație
Când se dezvoltă sumarea termenilor, eliminarea factorilor este destul de evidentă. În cazul în care pentru fiecare dintre cazuri, elementele opuse vor apărea în următoarea iterație.
Primul caz, (FX - Fx + 1), deoarece procesul funcționează într-un mod omolog pentru (Fx + 1-FX).
Dezvoltând primele 3 valori 1, 2, 3 se observă tendința de simplificare
X1 (F1 - F1 + 1) = F1 - FDouă
XDouă (FDouă - F2 + 1) = FDouă - F3
X3 (F3 - F3 + 1) = F3 - F4
Unde, atunci când exprimăm suma elementelor descrise:
X1 + XDouă + X3 = F1 - FDouă + FDouă - F3 + F3 - F4
Se observă că termenii FDouă și F3 sunt descrise împreună cu contrariile lor, ceea ce face ca simplificarea lor să fie inevitabilă. În același mod, se observă că termenii F1 și F4 rămâne.
Dacă suma a fost făcută de la x = 1 la x = 3, înseamnă că elementul F4 corespunde termenului generic Fn + 1.
Demonstrând astfel egalitatea:
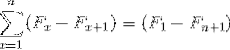
Cum se rezolvă?
Scopul însumărilor telescopice este de a facilita munca, astfel încât să nu fie necesar să se dezvolte un număr infinit de termeni sau să simplifice un lanț de adaosuri care este prea lung.
Pentru rezoluția sa va fi necesar doar să se evalueze termenii F.1 și Fn + 1. Aceste substituții simple alcătuiesc rezultatul final al însumării.
Totalitatea termenilor nu va fi exprimată, devenind necesară doar pentru demonstrarea rezultatului, dar nu și pentru procesul normal de calcul.
Important este să observăm convergența seriilor numerice. Uneori argumentul însumării nu va fi exprimat telescopic. În aceste cazuri, implementarea metodelor alternative de factoring este foarte frecventă..
Metoda caracteristică de factorizare în adaosurile telescopice este cea a fracțiilor simple. Acest lucru se întâmplă atunci când o fracție originală este descompusă într-o sumă de mai multe fracții, unde modelul telescopic (FX - Fx + 1) sau (Fx + 1 - FX).
Descompunerea în fracții simple
Pentru a verifica convergența seriilor numerice, este foarte comună transformarea expresiilor raționale cu metoda fracțiilor simple. Scopul este de a modela complotul în forma unei însumări telescopice..
De exemplu, următoarea egalitate reprezintă o descompunere în fracții simple:
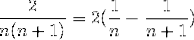
Când se dezvoltă seria numerică și se aplică proprietățile corespunzătoare, expresia ia următoarea formă:
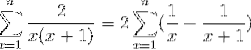
Unde forma telescopică (FX - Fx + 1).
Procedura este destul de intuitivă și constă în găsirea valorilor numărătorului care, fără a sparge egalitatea, permit separarea produselor care se află la numitor. Ecuațiile care apar în determinarea acestor valori sunt ridicate în funcție de comparații între ambele părți ale egalității.
Această procedură este respectată pas cu pas în dezvoltarea exercițiului 2.
Poveste
Este destul de incert să putem defini momentul istoric în care s-au prezentat sumele telescopice. Cu toate acestea, implementarea sa începe să fie văzută în secolul al XVII-lea, în studiile seriilor numerice efectuate de Leibniz și Huygens..
Ambii matematicieni, explorând însumările numerelor triunghiulare, încep să observe tendințe în convergența anumitor serii de elemente succesive. Dar și mai interesant este începutul modelării acestor expresii, în elemente care nu se succed neapărat.
De fapt, expresia utilizată anterior pentru a se referi la fracții simple:
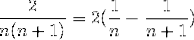
A fost introdus de Huygens și a atras imediat atenția lui Leibniz. Cine, în timp, a putut observa convergența la valoarea 2. Fără să știe, a implementat formatul de însumare telescopică.
Instruire
Exercitiul 1
Definiți la ce termen converge următoarea sumă:
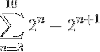
Când se dezvoltă manual suma, se observă următorul model:
(Două3 - Două4) + (24 - Două5) + (25 - Două6)… (Două10 - Douăunsprezece)
În cazul în care factorii de la 24 până la 210 Prezintă părți pozitive și negative, ceea ce face anularea lor evidentă. Atunci singurii factori care nu vor fi simplificați vor fi primii „23”Și ultimul„ 2unsprezece".
În acest fel, la implementarea criteriului de însumare telescopică, se obțin următoarele:
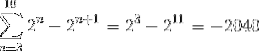
Exercițiul 2
Transformați argumentul într-o sumă de tip telescopic și definiți convergența seriei:
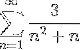
Așa cum se indică în enunț, primul lucru de făcut va fi să se descompună în fracții simple, pentru a reface argumentul și a-l exprima în mod telescopic..
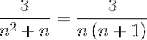
Trebuie să găsiți 2 fracții ai căror numitori sunt respectiv „n” și „n + 1”, unde metoda utilizată mai jos trebuie să obțină valorile numărătorului care îndeplinesc egalitatea.
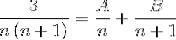
Procedăm la definirea valorilor lui A și B. Mai întâi, adăugați fracțiile.
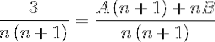
Apoi, numitorii sunt simplificați și se stabilește o ecuație liniară.
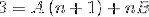
În pasul următor, se operează expresia din dreapta, până când se obține un model comparabil cu „3” din stânga..
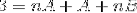
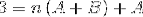
Pentru a defini ecuațiile care trebuie utilizate, trebuie comparate rezultatele ambelor părți ale egalității. Adică, nu sunt observate valori ale variabilei n în partea stângă, în acest fel A + B va trebui să fie egal cu zero.
A + B = 0; A = -B
Pe de altă parte, valoarea constantă A va trebui să fie egală cu valoarea constantă 3.
A = 3
Prin urmare.
A = 3 și B = -3
Odată ce valorile numărătorului pentru fracțiile simple au fost deja definite, suma este retratată.
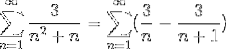
Acolo unde s-a realizat deja forma generică de însumare telescopică. Seria telescopică este dezvoltată.
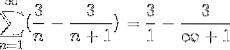
Unde, atunci când se împarte la un număr foarte mare, rezultatul se va apropia din ce în ce mai aproape de zero, observând convergența seriei la valoarea 3.
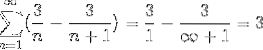
Acest tip de serie nu a putut fi rezolvat în alt mod, din cauza numărului infinit de iterații care definesc problema. Cu toate acestea, această metodă, împreună cu multe altele, încadrează ramura de studiu a seriilor numerice, al căror obiectiv este determinarea valorilor de convergență sau definirea divergenței seriilor menționate..
Referințe
- Lecții de calcul infinitesimal. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. EDITUM, 1994.
- Calcul integral: secvențe și serii de funcții. Antonio Rivera Figueroa. Grupo Editorial Patria, 21 oct. 2014.
- Un curs de calcul și analiză reală. Sudhir R. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5 iunie. 2006.
- Seria infinită. Fortul Tomlinson. The Clarendon Press, 1930.
- Elemente ale teoriei proceselor infinite. Lloyd Leroy Smail. Compania de carte McGraw-Hill, încorporată, 1923.



Nimeni nu a comentat acest articol încă.