
Dovada teoremei binomiale și exemple
teorema binomului este o ecuație care ne spune cum să dezvoltăm o expresie a formei (a + b)n pentru un număr natural n. Un binom nu este altceva decât suma a două elemente, cum ar fi (a + b). De asemenea, ne permite să știm pentru un termen dat de unkbn-k care este coeficientul care îl însoțește.
Această teoremă este atribuită în mod obișnuit inventatorului, fizicianului și matematicianului englez Sir Isaac Newton; Cu toate acestea, au fost găsite diferite înregistrări care indică faptul că existența sa era deja cunoscută în Orientul Mijlociu, în jurul anului 1000.

Indice articol
- 1 Numere combinatorii
- 2 Demo
- 3 Exemple
- 3.1 Identitatea 1
- 3.2 Identitatea 2
- 4 O altă demonstrație
- 4.1 Dovadă prin inducție
- 5 Curiozități
- 6 Referințe
Numere combinatorii
Teorema binomială ne spune matematic următoarele:
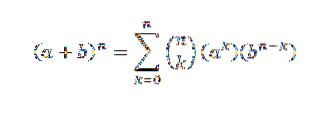
În această expresie a și b sunt numere reale și n este un număr natural.
Înainte de a da demonstrația, să ne uităm la câteva concepte de bază care sunt necesare.
Numărul combinatoriu sau combinațiile lui n în k se exprimă după cum urmează:
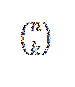
Această formă exprimă valoarea câte subseturi cu k elemente pot fi alese dintr-un set de n elemente. Expresia sa algebrică este dată de:
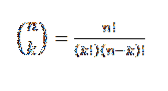
Să vedem un exemplu: să presupunem că avem un grup de șapte bile, dintre care două sunt roșii și restul sunt albastre..
Vrem să știm câte modalități le putem aranja la rând. O modalitate ar putea fi plasarea celor două roșii în prima și a doua poziție, iar restul mingilor în pozițiile care rămân..
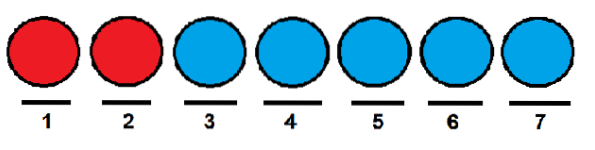
Similar cu cazul precedent, am putea da bilelor roșii prima și respectiv ultima poziție și le putem ocupa pe celelalte cu bile albastre.
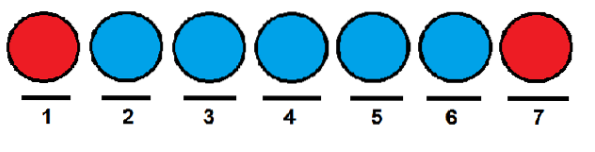
Acum, o modalitate eficientă de a număra câte modalități putem aranja bilele la rând este folosind numere combinatorii. Putem vedea fiecare poziție ca un element al următorului set:
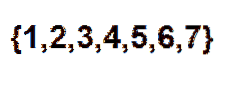
Apoi rămâne doar să alegeți un subset de două elemente, în care fiecare dintre aceste elemente să reprezinte poziția pe care o vor ocupa bilele roșii. Putem face această alegere în funcție de relația dată de:
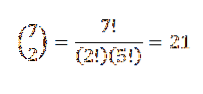
În acest fel, avem că există 21 de moduri de a comanda aceste bile.
Ideea generală a acestui exemplu va fi foarte utilă pentru a demonstra teorema binomului. Să vedem un caz particular: dacă n = 4, avem (a + b)4, care nu este altceva decât:
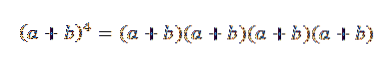
Când dezvoltăm acest produs, rămânem cu suma termenilor obținuți înmulțind un element din fiecare dintre cei patru factori (a + b). Astfel, vom avea termeni care vor avea forma:
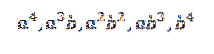
Dacă am vrea să obținem termenul din forma a4, doar înmulțiți-vă după cum urmează:
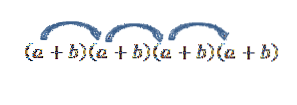
Rețineți că există o singură modalitate de a obține acest element; dar, ce se întâmplă dacă acum căutăm termenul formei aDouăbDouă? Deoarece „a” și „b” sunt numere reale și, prin urmare, legea comutativă este valabilă, avem o singură modalitate de a obține acest termen este să înmulțim cu membrii așa cum este indicat de săgeți.
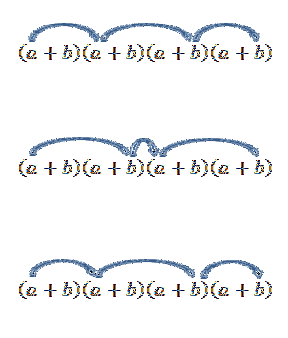
Efectuarea tuturor acestor operațiuni este de obicei oarecum plictisitoare, dar dacă vedem termenul „a” ca o combinație în care vrem să știm câte modalități putem alege doi „a” dintr-un set de patru factori, putem folosi ideea din exemplu anterior. Deci, avem următoarele:
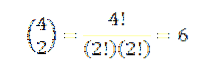
Astfel, știm că în expansiunea finală a expresiei (a + b)4 vom avea exact 6aDouăbDouă. Folosind aceeași idee pentru celelalte elemente, trebuie să:
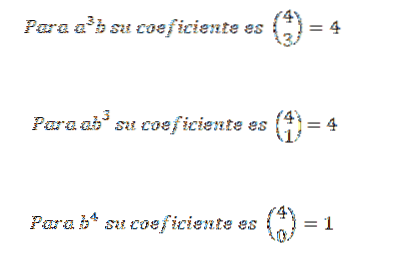
Apoi adăugăm expresiile obținute anterior și avem că:
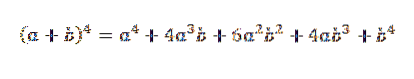
Este o dovadă formală pentru cazul general în care „n” este orice număr natural.
Demonstrație
Rețineți că termenii care rămân la dezvoltarea (a + b)n Sunt de forma akbn-k, unde k = 0,1, ..., n. Folosind ideea exemplului anterior, avem modalitatea de a alege „k” variabile „a” dintre factorii „n” este:
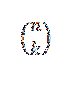
Alegând în acest fel, alegem automat n-k variabile „b”. Din aceasta rezultă că:
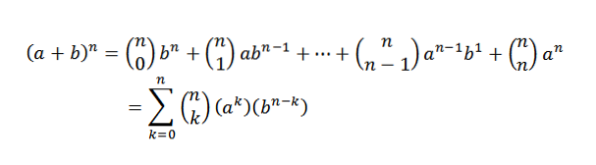
Exemple
Luând în considerare (a + b)5, Care ar fi dezvoltarea ta?
Prin teorema binomului avem:
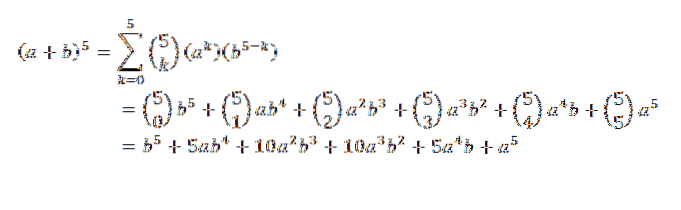
Teorema binomului este foarte utilă dacă avem o expresie în care vrem să știm care este coeficientul unui anumit termen fără a fi nevoie să facem expansiunea completă. Ca exemplu putem lua următoarea necunoscută: care este coeficientul lui x7Da9 în expansiunea lui (x + y)16?
Prin teorema binomului, avem că coeficientul este:
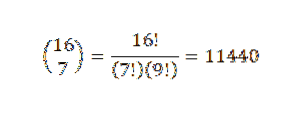
Un alt exemplu ar fi: care este coeficientul lui x5Da8 în dezvoltarea (3x-7y)13?
Mai întâi rescriem expresia într-un mod convenabil; aceasta este:
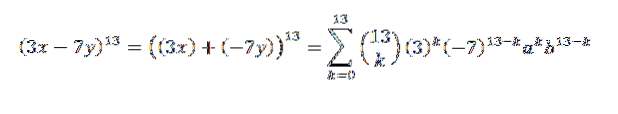
Apoi, folosind teorema binomială, avem că coeficientul căutat este atunci când avem k = 5
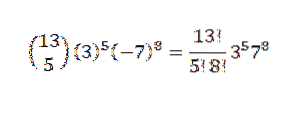
Un alt exemplu al utilizărilor acestei teoreme se află în dovada unor identități comune, precum cele pe care le vom menționa mai jos.
Identitate 1
Dacă „n” este un număr natural, avem:
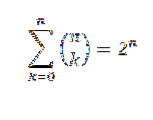
Pentru demonstrație folosim teorema binomială, unde atât „a”, cât și „b” iau valoarea 1. Apoi avem:
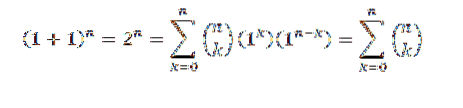
În acest fel am dovedit prima identitate.
Identitate 2
Dacă „n” este un număr natural, atunci
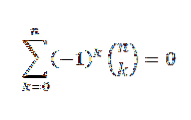
Prin teorema binomului avem:
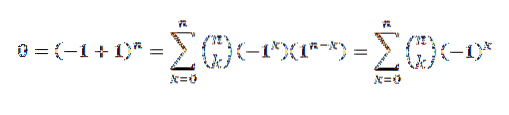
O altă demonstrație
Putem face o altă dovadă pentru teorema binomială folosind metoda inductivă și identitatea lui Pascal, care ne spune că, dacă „n” și „k” sunt numere întregi pozitive care satisfac n ≥ k, atunci:
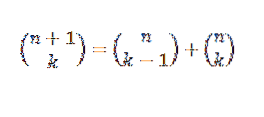
Dovadă de inducție
Mai întâi să vedem că baza inductivă se menține. Dacă n = 1, avem:
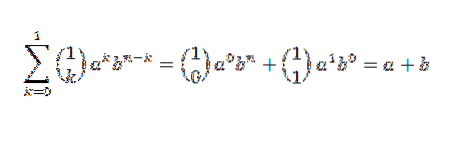
Într-adevăr, vedem că se împlinește. Acum, să fie n = j astfel încât:
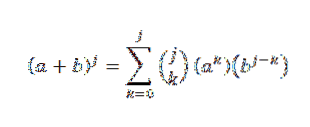
Vrem să vedem că pentru n = j + 1 este adevărat că:
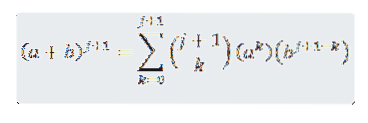
Deci trebuie să:
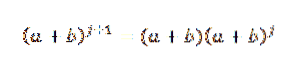
Prin ipoteză știm că:
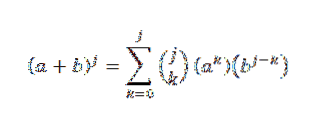
Apoi, folosind proprietatea distributivă:
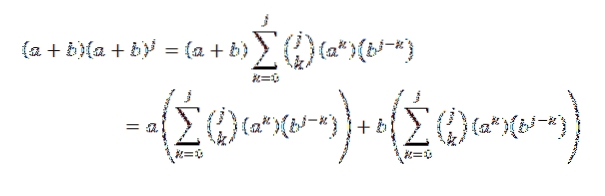
Ulterior, dezvoltând fiecare dintre rezumări, avem:
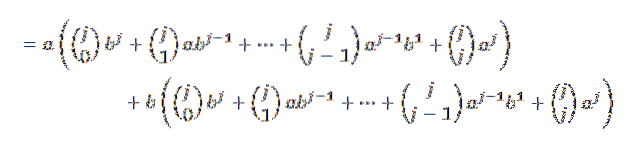
Acum, dacă grupăm într-un mod convenabil, avem:
Folosind identitatea pascal, avem:
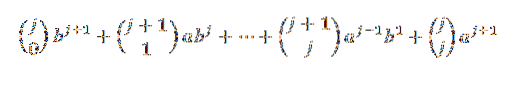
În cele din urmă, rețineți că:
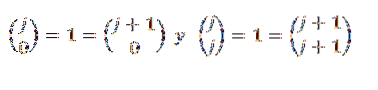
Prin urmare, vedem că teorema binomială este valabilă pentru toate „n” aparținând numerelor naturale și, cu aceasta, dovada se încheie.
Curiozități
Numărul combinatoriu (nk) se mai numește coeficient binomial deoarece tocmai coeficientul apare în dezvoltarea binomului (a + b)n.
Isaac Newton a dat o generalizare a acestei teoreme pentru cazul în care exponentul este un număr real; această teoremă este cunoscută sub numele de teorema binomială a lui Newton.
În cele mai vechi timpuri, acest rezultat era cunoscut pentru cazul particular în care n = 2. Acest caz este menționat în Elemente de Euclid.
Referințe
- Johnsonbaugh Richard. Matematică discretă. PHH
- Kenneth.H. Rosen.Matematica discretă și aplicațiile sale. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Dr. Seymour Lipschutz și Marc Lipson. Matematică discretă. McGRAW-HILL.
- Ralph P. Grimaldi. Matematică discretă și combinatorică. Addison-Wesley Iberoamericana
- Verde Star Luis ... Matematică discretă și combinatorie. Anthropos



Nimeni nu a comentat acest articol încă.