
A treia lege a formulelor termodinamice, ecuații, exemple
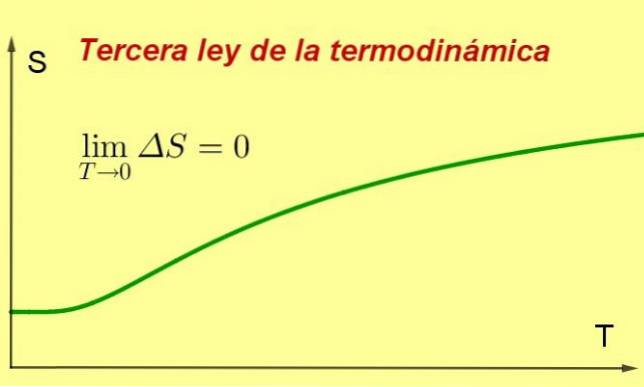
A treia lege a termodinamicii afirmă că entropia unui sistem termodinamic închis în echilibru tinde să fie minimă și constantă, deoarece temperatura sa se apropie de 0 kelvin.
Această valoare de entropie va fi independentă de variabilele sistemului (presiune sau câmp magnetic aplicat, printre altele). Ceea ce se întâmplă este că, deoarece temperatura este mai aproape de 0 K, procesele din sistem se opresc și, deoarece entropia este o măsură a agitației interne, aceasta scade în mod necesar.
Indice articol
- 1 Concepte anterioare
- 1.1 Sistem termodinamic
- 1.2 Sisteme izolate, închise sau deschise
- 1.3 Macrostate și microstate
- 2 Formule și ecuații
- 2.1 Calculul entropiei absolute a unei substanțe
- 3 Aplicații
- 3.1 Entropia unui sistem la temperatură scăzută
- 3.2 Entropia reziduală
- 4 Exemple
- 4.1 Exemplul 1: zero absolut și nedeterminarea lui Heisenberg
- 4.2 Exemplul 2: Superfluiditatea și cazul ciudat al heliului-4
- 5 Exerciții rezolvate
- 5.1 - Exercițiul 1
- 5.2 - Exercițiul 2
- 6 Referințe
Concepte anterioare
Pentru a înțelege sfera celei de-a treia legi a termodinamicii, relevantă la temperaturi foarte scăzute, este necesar să se revizuiască următoarele concepte:
Sistem termodinamic
În general se referă la un gaz, un lichid sau un solid. Ceea ce nu face parte din sistem se numește mediu inconjurator. Cel mai comun sistem termodinamic este gazul ideal, care constă din N particule (atomi) care interacționează numai prin coliziuni elastice.
Sisteme izolate, închise sau deschise
Sistemelor izolate nu le este permis niciun schimb cu mediul. Sistemele închise nu schimbă materia cu mediul, dar schimbă căldura. În cele din urmă, sistemele deschise pot schimba atât materia, cât și căldura cu mediul..
Macrostate și microstate
Macrostatul unui sistem este setul de valori pe care le au variabilele sale: presiune, temperatură, volum, număr de moli, entropie și energie internă. Pe de altă parte, microstatul - în cazul unui gaz ideal -, este dat de poziția și impulsul fiecăreia dintre N particule care îl formează, la un moment dat.
Multe microstate pot avea ca rezultat aceeași macrostată. Într-un gaz la temperatura camerei, numărul de microstate posibile este imens, deoarece numărul de particule care îl compun, diferitele poziții și diferitele energii pe care le pot adopta este foarte mare..
Formule și ecuații
Entropia, așa cum am spus, este o variabilă macroscopică termodinamică care măsoară gradul de tulburare moleculară a sistemului. Gradul de tulburare al unui sistem este mai mare cu cât numărul de posibile microstate este mai mare.
Acest concept este necesar pentru a formula a treia lege a termodinamicii sub formă matematică. Fie S entropia sistemului, atunci:

Entropia este o variabilă de stare macroscopică, care este direct legată de numărul de posibile microstate ale unui sistem, prin următoarea formulă:
S = k ln (W)
În ecuația de mai sus: S reprezintă entropie, W numărul de posibile microstate ale sistemului și k este constanta lui Boltzmann (k = 1,38 x 10-2. 3 J / K). Adică entropia unui sistem este k ori logaritmul natural al numărului de microstate posibile.
Calculul entropiei absolute a unei substanțe
Este posibil să se definească entropia absolută a unei substanțe pure pornind de la definiția variației entropiei:

δQ = n. cp .dT
Aici cp este căldura specifică molară și n numărul de moli. Dependența căldurii specifice molare de temperatură este o informație obținută experimental și cunoscută pentru multe substanțe pure..
Conform celei de-a treia legi a substanțelor pure:


Aplicații
În viața de zi cu zi, a treia lege a termodinamicii are puține aplicații, tocmai opusul primei și celei de-a doua legi. Acest lucru se datorează faptului că este un principiu care se referă la ceea ce se întâmplă într-un sistem atunci când se apropie de 0 absolut, un interval de temperatură rar.
De fapt, atingerea 0 absolută sau -273,15 ° C este imposibilă (a se vedea exemplul 1 de mai jos). Cu toate acestea, a treia lege se aplică atunci când se studiază răspunsul materialelor la temperaturi foarte scăzute.
Datorită acestui fapt, au apărut progrese importante în fizica materiei condensate, cum ar fi:
-Superfluiditate (vezi exemplul 2 de mai jos)
-Superconductivitate
-Tehnici de răcire cu laser
-Condensat Bose-Einstein
-Gazele superfluide Fermi.

La temperaturi extrem de scăzute, scăderea entropiei permite apariția unor fenomene cuantice interesante. Prin urmare, să vedem ce se întâmplă cu entropia unui sistem la temperatură foarte scăzută.
Entropia unui sistem la temperatură scăzută
Când aveți o substanță cristalină perfectă, entropia sa minimă este exact zero, deoarece este un sistem foarte ordonat. La temperaturi apropiate de 0 absolut, materia se află într-o stare condensată (lichidă sau solidă), iar vibrațiile din cristal sunt minime.
Unii autori consideră că o afirmație alternativă a celei de-a treia legi a termodinamicii este următoarea:
"Dacă materia se condensează pentru a forma un cristal perfect, atunci când temperatura tinde la zero absolut, entropia tinde la exact zero".
Să clarificăm câteva aspecte ale afirmației anterioare:
- Un cristal perfect este acela în care fiecare moleculă este identică și în care structura moleculară se repetă identic în întregime..
- Pe măsură ce temperatura se apropie de zero absolut, vibrația atomică scade aproape complet.
Apoi cristalul formează o singură configurație sau un posibil microstat, adică W = 1, și, prin urmare, entropia este egală cu zero:
S = k ln (1) = 0
Dar nu întotdeauna un material răcit aproape de zero absolut formează un cristal, cu atât mai puțin acest cristal este perfect. Acest lucru se întâmplă numai dacă procesul de răcire este foarte lent și reversibil..
În caz contrar, factori precum impuritățile prezente în sticlă ar face posibilă existența altor microstate. Prin urmare, W> 1 și entropia ar fi mai mare decât 0.
Entropia reziduală
Dacă procesul de răcire este brusc, în timpul acestuia sistemul trece printr-o succesiune de stări de neechilibru, care duc la materializarea vitrificării. În acest caz, nu se produce o structură cristalină ordonată, ci un solid amorf, a cărui structură este similară cu cea a unui lichid..
În acest caz, valoarea minimă a entropiei în vecinătatea zero absolut nu este zero, deoarece numărul de microstate este considerabil mai mare de 1. Diferența dintre această entropie și entropia nulă a stării cristaline perfecte este cunoscută sub numele de entropie reziduală.
Explicația este că sub o anumită temperatură prag, sistemul nu are altă opțiune decât să ocupe microstatele cu energie mai mică, care, deoarece sunt cuantificate, constituie un număr fix.
Se vor ocupa de menținerea entropiei constante, chiar și atunci când temperatura continuă să scadă până la zero absolut..
Exemple
Exemplul 1: zero absolut și nedeterminarea lui Heisenberg
Principiul de nedeterminare al lui Heisenberg stabilește că incertitudinea în poziția și impulsul unei particule, de exemplu în atomii unei rețele de cristal, nu sunt independente una de cealaltă, ci urmează mai degrabă următoarea inegalitate:
Δx ⋅ Δp ≥ h
Unde h este constanta lui Planck. Adică, incertitudinea în poziție înmulțită cu incertitudinea în impuls (masa de viteză) este mai mare sau egală cu constanta lui Planck, a cărei valoare este foarte mică, dar nu zero: h = 6,63 x 10-3. 4 J s.
Și ce legătură are principiul incertitudinii cu a treia lege a termodinamicii? Dacă poziția atomilor din rețeaua cristalină este fixă și precisă (Δx = 0) atunci viteza acestor atomi poate lua orice valoare între 0 și infinit. Acest lucru este contrazis de faptul că la zero absolut, orice mișcare de agitație termică încetează..
Reciproc, dacă presupunem că la temperatura zero absolută, orice agitație încetează și impulsul fiecărui atom din rețea este exact zero (Δp = 0), atunci principiul incertitudinii Heisenberg ar implica faptul că nedeterminarea în pozițiile fiecărui atom ar fi infinită, adică pot fi în orice poziție.
Ca o consecință a afirmației anterioare, numărul de microstate ar tinde spre infinit, iar entropia ar lua, de asemenea, o valoare nedeterminată.
Exemplul 2: Superfluiditatea și cazul ciudat al heliului-4
În superfluiditate, care apare la temperaturi foarte scăzute, materia pierde fricțiunea internă dintre moleculele sale, numită viscozitate. Într-un astfel de caz, fluidul ar putea circula fără frecare pentru totdeauna, dar problema este că la aceste temperaturi aproape nimic nu este lichid, cu excepția heliului..
Heliul și heliul 4 (izotopul său cel mai abundent) constituie un caz unic, deoarece la presiunea atmosferică și la temperaturi apropiate de zero absolut, heliul rămâne lichid.
Când heliul-4 este supus la o temperatură sub 2,2 K la presiunea atmosferică devine o superfluid. Această descoperire a avut loc în 1911 la Leyden de către fizicianul olandez Heike Kamerlingh Onnes (1853-1926).
Atomul de heliu-4 este un boson. Bosonii, spre deosebire de fermioni, sunt particule care pot ocupa toate aceeași stare cuantică. Prin urmare, bosonii nu îndeplinesc principiul excluderii Pauli.
Atunci toți atomii de heliu-4 la temperaturi sub 2,2 K ocupă aceeași stare cuantică și, prin urmare, există un singur microstat posibil, ceea ce înseamnă că heliul-4 superfluid are S = 0.
Exerciții rezolvate
- Exercitiul 1
Să luăm în considerare un caz simplu care constă dintr-un sistem format din doar trei particule care au trei niveluri de energie. Pentru acest sistem simplu:
a) Determinați numărul de microstate posibile pentru trei domenii de temperatură:
-înalt
-Jumătate
-Mic de statura
b) Determinați prin intermediul ecuației Boltzmann entropia în diferitele intervale de temperatură.
c) Discutați rezultatele și explicați dacă acestea contravin sau nu legii a treia a termodinamicii..
Solutie la
La scară moleculară și atomică, energiile pe care le poate adopta un sistem sunt cuantificate, ceea ce înseamnă că pot lua doar anumite valori discrete. În plus, atunci când temperaturile sunt atât de scăzute, particulele care alcătuiesc sistemul au doar posibilitatea de a ocupa cele mai scăzute niveluri de energie..
Temperatura ridicata
Dacă sistemul are o temperatură relativ ridicată T, atunci particulele au suficientă energie pentru a ocupa orice nivel disponibil, dând naștere la 10 posibile microstate, care apar în figura următoare:
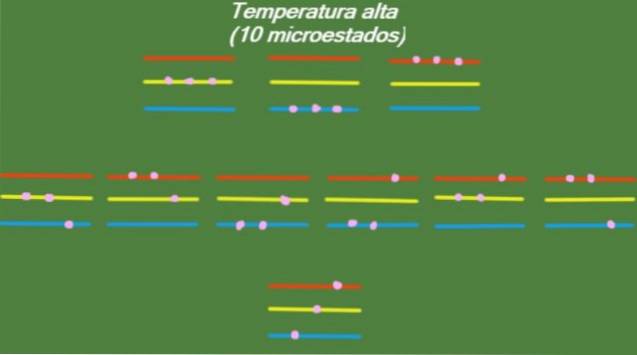
Temperatura medie
În cazul în care sistemul are o temperatură intermediară, atunci particulele care îl compun nu au suficientă energie pentru a ocupa cel mai înalt nivel de energie. Posibilele microstate sunt ilustrate în figură:
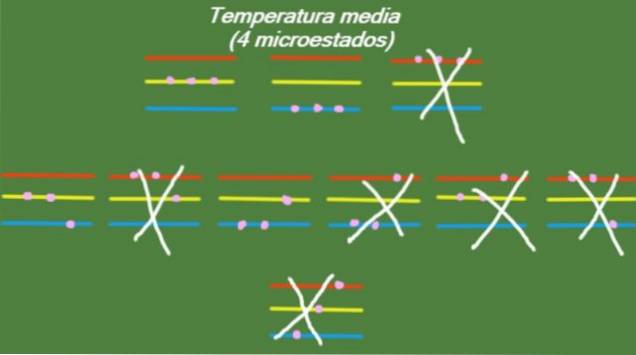
Temperatura scazuta
Dacă temperatura continuă să scadă în sistemul nostru idealizat de trei particule și trei niveluri de energie, atunci particulele vor avea atât de puțină energie încât vor putea ocupa doar cel mai scăzut nivel. În acest caz, rămâne doar 1 microstat posibil, așa cum se arată în figura 6:
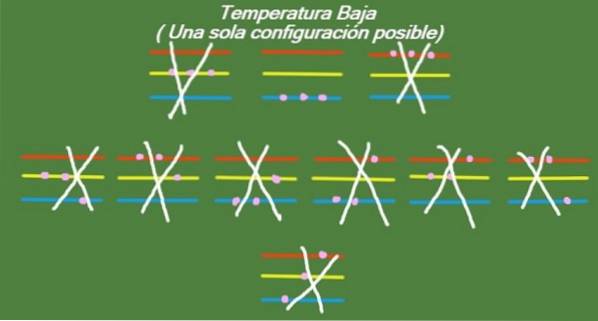
Soluția b
Odată ce numărul microstatelor din fiecare interval de temperatură este cunoscut, putem folosi acum ecuația Boltzmann dată mai sus pentru a găsi entropia în fiecare caz.
S = k ln (10) = 2,30 x k = 3,18 x 10-2. 3 J / K (Temperatura ridicata)
S = k ln (4) = 1,38 x k = 1,92 x 10-2. 3 J / K (Temperatura medie)
Și, în sfârșit:
S = k ln (1) = 0 (Temperatura scazuta)
Soluția c
Mai întâi observăm că entropia scade odată cu scăderea temperaturii, așa cum era de așteptat. Dar pentru cele mai mici valori de temperatură se atinge o valoare prag, de la care se atinge starea de bază a sistemului..
Chiar și atunci când temperatura este cât mai aproape de zero absolut, nu există stări de energie mai mici disponibile. Apoi, entropia își păstrează valoarea minimă constantă, care în exemplul nostru este S = 0.
Acest exercițiu ilustrează, la nivelul microstatului unui sistem, motivul pentru care se menține a treia lege a termodinamicii..
- Exercițiul 2
Motivați dacă următoarea afirmație este adevărată sau falsă:
"Entropia unui sistem la temperatura zero absolută este exact zero".
Justificați-vă răspunsul și descrieți câteva exemple.
Soluţie
Răspunsul este: fals.
În primul rând, 0 absolut al temperaturii nu poate fi atins deoarece ar încălca principiul incertitudinii lui Heisenberg și a treia lege a termodinamicii..
Este foarte important să rețineți că a treia lege nu spune ce se întâmplă la 0 absolut, ci mai degrabă atunci când temperatura este infinit de aproape de 0 absolut. Diferența este subtilă, dar semnificativă.
Nici cea de-a treia lege nu afirmă că atunci când temperatura ia o valoare în mod arbitrar aproape de zero absolut, entropia tinde la zero. Acest lucru s-ar produce numai în cazul analizat anterior: cristalul perfect, care este o idealizare.
Multe sisteme la scară microscopică, adică la scară cuantică, au nivelul lor de bază de energie degenerat, ceea ce înseamnă existența diferitelor setări la cel mai scăzut nivel de energie.
Aceasta înseamnă că în aceste sisteme entropia nu ar fi niciodată exact zero. Nici entropia nu ar fi exact zero în sistemele care se vitrifică atunci când temperatura tinde la zero absolut. În acest caz, entropie reziduală înainte văzut.
Se datorează faptului că moleculele sale au fost „blocate” înainte de a atinge cele mai scăzute niveluri de energie disponibile, ceea ce crește considerabil numărul de microstate posibile, făcând imposibil ca entropia să fie exact zero..
Referințe
- Cengel, Y. 2012. Termodinamică. Ediția a VII-a. McGraw Hill. 347.
- Laboratorul de propulsie cu jet. Cel mai tare loc din Univers. Adus de la: coldatomlab.jpl.nasa.gov.
- González, A. Entropie și spontaneitate. Recuperat de la: geocities.ws
- Quora. Care este utilizarea practică a celei de-a treia legi a termodinamicii? Recuperat de pe: quora.com
- Chimie generală. Al treilea principiu al termodinamicii. Recuperat de pe: corinto.pucp.edu.pe
- A treia lege a termodinamicii. Recuperat de pe: youtube.com
- Wikipedia. Entropia reziduală. Recuperat de pe: en.wikipedia.com
- Wikipedia. A treia lege a termodinamicii. Recuperat de pe: en.wikipedia.com



Nimeni nu a comentat acest articol încă.