
Definiția transformării Laplace, istoria și pentru ce este ea
Transformarea Laplace În ultimii ani a avut o mare importanță în studiile de inginerie, matematică și fizică, printre alte domenii științifice, deoarece, pe lângă faptul că este de mare interes teoretic, oferă o modalitate simplă de a rezolva problemele care provin din știință și inginerie..
Inițial transformata Laplace a fost prezentată de Pierre-Simón Laplace în studiul său despre teoria probabilității și a fost inițial tratată ca un obiect matematic de interes pur teoretic..

Aplicațiile actuale apar atunci când diverși matematicieni au încercat să ofere o justificare formală „regulilor operaționale” folosite de Heaviside în studiul ecuațiilor teoriei electromagnetice..
Indice articol
- 1 Definiție
- 1.1 Exemple
- 1.2 Teorema (Condiții suficiente pentru existență)
- 1.3 Transformarea Laplace a unor funcții de bază
- 2 Istorie
- 2.1 1782, Laplace
- 2.2 Oliver Heaviside
- 3 Proprietăți
- 3.1 Liniaritatea
- 3.2 Teorema primei traduceri
- 3.3 A doua teoremă de traducere
- 3.4 Schimbarea scalei
- 3.5 Transformata Laplace a derivatelor
- 3.6 Transformata Laplace a integralelor
- 3.7 Înmulțirea cu tn
- 3.8 Împărțirea după t
- 3.9 Funcții periodice
- 3.10 Comportamentul lui F (s) ca s tinde spre infinit
- 4 Transformări inverse
- 4.1 Exercițiu
- 5 Aplicații ale transformatei Laplace
- 5.1 Ecuații diferențiale
- 5.2 Sisteme de ecuații diferențiale
- 5.3 Mecanică și circuite electrice
- 6 Referințe
Definiție
Fie f o funcție definită pentru t ≥ 0. Transformata Laplace este definită după cum urmează:
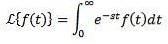
Se spune că transformata Laplace există dacă integrala anterioară converge, altfel se spune că transformata Laplace nu există.
În general, litere mici sunt folosite pentru a indica funcția care urmează să fie transformată, iar litera mare corespunde transformării sale. În acest fel vom avea:
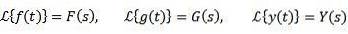
Exemple
Luați în considerare funcția constantă f (t) = 1. Avem că transformarea sa este:
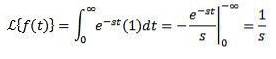
Ori de câte ori integrala converge, adică ori de câte ori s> 0. În caz contrar, s < 0, la integral diverge.
Fie g (t) = t. Transformarea sa Laplace este dată de
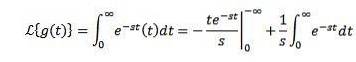
Prin integrarea pe părți și știind că tu-Sf tinde la 0 când t tinde spre infinit și s> 0, împreună cu exemplul anterior avem:
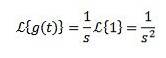
Transformarea poate exista sau nu, de exemplu pentru funcția f (t) = 1 / t integrala care definește transformata sa Laplace nu converge și, prin urmare, transformarea sa nu există.
Condițiile suficiente pentru a garanta existența transformării Laplace a unei funcții f sunt că f este continuu în părți pentru t ≥ 0 și este de ordin exponențial.
Se spune că o funcție este continuă în bucăți pentru t ≥ 0, când pentru orice interval [a, b] cu a> 0, există un număr finit de puncte tk, unde f are discontinuități și este continuu în fiecare subinterval [tk-1,tk].
Pe de altă parte, se spune că o funcție este de ordin exponențial c dacă există constante reale M> 0, c și T> 0 astfel încât:
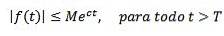
Ca exemple avem că f (t) = tDouă este de ordin exponențial, deoarece | tDouă| < e3t pentru toate t> 0.
Într-un mod formal, avem următoarea teoremă
Teorema (Condiții suficiente pentru existență)
Dacă f este o funcție parțială continuă pentru t> 0 și de ordin exponențial c, atunci există transformata Laplace pentru s> c.
Este important să rețineți că aceasta este o condiție de suficiență, adică ar putea fi cazul în care există o funcție care nu îndeplinește aceste condiții și chiar și așa există transformata sa Laplace.
Un exemplu în acest sens este funcția f (t) = t-1/2 care nu este continuu în bucăți pentru t ≥ 0, dar există transformata sa Laplace.
Transformarea Laplace a unor funcții de bază
Tabelul următor prezintă transformatele Laplace ale celor mai comune funcții.

Poveste
Transformarea Laplace își datorează numele lui Pierre-Simon Laplace, un matematician și astronom teoretic francez care s-a născut în 1749 și a murit în 1827. Faima sa a fost de așa natură încât a fost cunoscut sub numele de Newton al Franței.
În 1744 Leonard Euler și-a dedicat studiile integrale cu forma
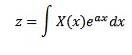
ca soluții de ecuații diferențiale obișnuite, dar a abandonat rapid această investigație. Mai târziu, Joseph Louis Lagrange, care l-a admirat foarte mult pe Euler, a investigat și acest tip de integrale și le-a legat de teoria probabilității.
1782, Laplace
În 1782 Laplace a început să studieze aceste integrale ca soluții la ecuații diferențiale și, conform istoricilor, în 1785 a decis reformularea problemei, care a dat naștere ulterior transformărilor Laplace așa cum sunt înțelese astăzi..
Fiind introdus în câmpul teoriei probabilității, acesta a fost de puțin interes pentru oamenii de știință din epocă și a fost văzut doar ca un obiect matematic de interes teoretic..
Oliver Heaviside
A fost la mijlocul secolului al XIX-lea când inginerul englez Oliver Heaviside a descoperit că operatorii diferențiali pot fi tratați ca variabile algebrice, oferind astfel Laplace transformă aplicația lor modernă..
Oliver Heaviside a fost un fizician, inginer electric și matematician englez care s-a născut la Londra în 1850 și a murit în 1925. În timp ce încerca să rezolve problemele ecuației diferențiale aplicate teoriei vibrațiilor și folosind studiile lui Laplace, el a început să modeleze aplicațiile moderne ale transformatelor Laplace..
Rezultatele prezentate de Heaviside s-au răspândit rapid în întreaga comunitate științifică a vremii, dar întrucât munca sa nu a fost riguroasă, a fost rapid criticat de matematicienii mai tradiționali..
Cu toate acestea, utilitatea muncii lui Heaviside în rezolvarea ecuațiilor din fizică a făcut ca metodele sale să fie populare printre fizicieni și ingineri..
În ciuda acestor eșecuri și după câteva decenii de încercări eșuate, la începutul secolului al XX-lea o justificare riguroasă ar putea fi dată regulilor operaționale date de Heaviside..
Aceste încercări au dat roade datorită eforturilor diferiților matematicieni precum Bromwich, Carson, van der Pol, printre altele..
Proprietăți
Printre proprietățile transformatei Laplace, se evidențiază următoarele:
Linearitatea
Fie c1 și c2 constante și funcțiile f (t) și g (t) ale căror transformate Laplace sunt F (s) și respectiv G (s), atunci avem:
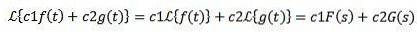
Datorită acestei proprietăți, se spune că transformata Laplace este un operator liniar.
Exemplu
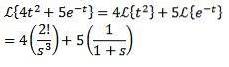
Teorema primei traduceri
Dacă se întâmplă că:
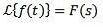
Și „a” este orice număr real, deci:
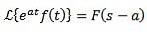
Exemplu
Deoarece transformata Laplace a cos (2t) = s / (s ^ 2 + 4) atunci:
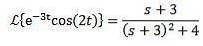
A doua teoremă de traducere
da
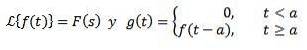
Atunci
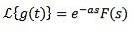
Exemplu
Dacă f (t) = t ^ 3, atunci F (s) = 6 / s ^ 4. Și, prin urmare, transformarea
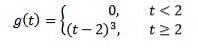
este G (s) = 6e-2s/ s ^ 4
Schimbarea scalei
da
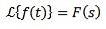
Și „a” este un real care nu este zero, trebuie
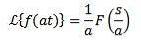
Exemplu
Deoarece transformarea lui f (t) = sin (t) este F (s) = 1 / (s ^ 2 + 1) avem
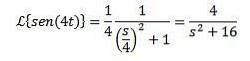
Transformata Laplace a derivatelor
Dacă f, f ', f ", ..., f(n) sunt continue pentru t ≥ 0 și sunt de ordin exponențial și f(n)(t) este continuu în bucăți pentru t ≥ 0, atunci
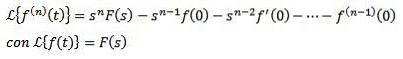
Transformarea Laplace a integralelor
da
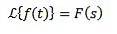
Atunci
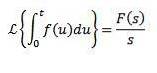
Înmulțirea cu tn
Dacă trebuie
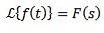
Atunci
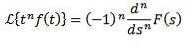
Împărțirea după t
Dacă trebuie
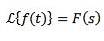
Atunci
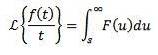
Funcții periodice
Fie f o funcție periodică cu perioada T> 0, adică f (t + T) = f (t), atunci
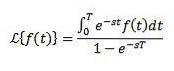
Comportamentul lui F (s) ca s tinde spre infinit
Dacă f este continuu în părți și de ordine exponențială și
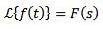
Atunci
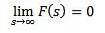
Transformări inverse
Când aplicăm transformata Laplace la o funcție f (t) obținem F (s), care reprezintă transformata menționată. În același mod putem spune că f (t) este transformata Laplace inversă a lui F (s) și este scrisă ca
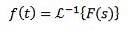
Știm că transformările Laplace ale lui f (t) = 1 și g (t) = t sunt F (s) = 1 / s și G (s) = 1 / sDouă respectiv, de aceea trebuie
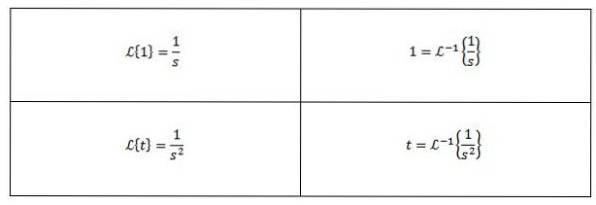
Unele transformate Laplace inverse comune sunt după cum urmează

Mai mult, transformata Laplace inversă este liniară, adică este adevărat că
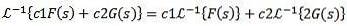
Exercițiu
Găsi
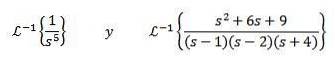
Pentru a rezolva acest exercițiu trebuie să potrivim funcția F (s) cu una din tabelul anterior. În acest caz, dacă luăm n + 1 = 5 și folosind proprietatea de liniaritate a transformatei inverse, înmulțim și împărțim la 4! Obținerea
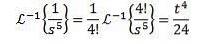
Pentru a doua transformare inversă aplicăm fracții parțiale pentru a rescrie funcția F (s) și apoi proprietatea liniarității, obținând
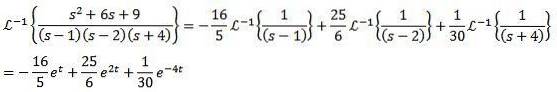
După cum putem vedea din aceste exemple, este obișnuit ca funcția F (e) evaluată să nu se potrivească cu exactitate cu niciuna dintre funcțiile date în tabel. Pentru aceste cazuri, după cum se poate observa, este suficient să rescrieți funcția până la atingerea formei corespunzătoare.
Aplicații ale transformatei Laplace
Ecuatii diferentiale
Principala aplicație a transformatelor Laplace este rezolvarea ecuațiilor diferențiale.
Folosind proprietatea de transformare a unei derivate este clar că
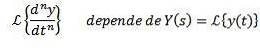
Iar din derivatele n-1 evaluate la t = 0.
Această proprietate face transformarea foarte utilă pentru rezolvarea problemelor de valoare inițială în care sunt implicate ecuații diferențiale cu coeficienți constanți..
Următoarele exemple arată cum se folosește transformata Laplace pentru a rezolva ecuații diferențiale.
Exemplul 1
Având în vedere următoarea problemă de valoare inițială
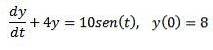
Folosiți transformata Laplace pentru a găsi soluția.
Aplicăm transformata Laplace fiecărui membru al ecuației diferențiale
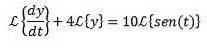
Prin proprietatea transformării unei derivate avem
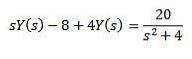
Dezvoltând toată expresia și ștergând Y (s) suntem lăsați
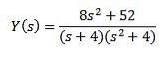
Folosind fracții parțiale pentru a rescrie partea dreaptă a ecuației pe care o obținem
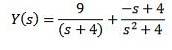
În cele din urmă, scopul nostru este să găsim o funcție y (t) care să satisfacă ecuația diferențială. Utilizarea transformatei Laplace inversă ne dă rezultatul
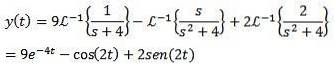
Exemplul 2
Rezolva
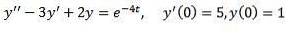
Ca și în cazul anterior, aplicăm transformarea pe ambele părți ale ecuației și separăm termen cu termen.
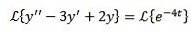
În acest fel avem ca rezultat
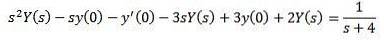
Înlocuirea cu valorile inițiale date și rezolvarea pentru Y (s)
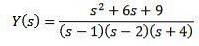
Folosind fracții simple putem rescrie ecuația după cum urmează
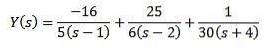
Iar aplicarea transformatei Laplace inversă ne dă rezultatul
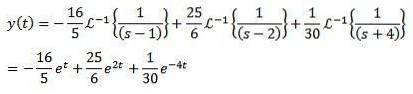
În aceste exemple, ați putea ajunge la concluzia greșită că această metodă nu este mult mai bună decât metodele tradiționale de rezolvare a ecuațiilor diferențiale..
Avantajele transformării Laplace sunt că nu trebuie să utilizați variația parametrilor sau să vă faceți griji cu privire la diferitele cazuri ale metodei coeficientului nedeterminat..
În plus, la rezolvarea problemelor de valoare inițială prin această metodă, de la început folosim condițiile inițiale, deci nu este necesar să se efectueze alte calcule pentru a găsi soluția specială.
Sisteme de ecuații diferențiale
Transformata Laplace poate fi de asemenea utilizată pentru a găsi soluții la ecuații diferențiale ordinare simultane, așa cum arată exemplul următor.
Exemplu
Rezolvă
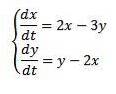
Cu condițiile inițiale x (0) = 8 și y (0) = 3.
Dacă trebuie
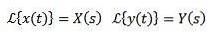
Atunci
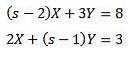
Rezolvarea ne dă ca rezultat
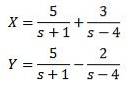
Și aplicând transforma Laplace inversă pe care o avem
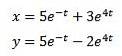
Mecanică și circuite electrice
Transformata Laplace are o mare importanță în fizică, are în principal aplicații pentru mecanică și circuite electrice.
Un circuit electric simplu este alcătuit din următoarele elemente
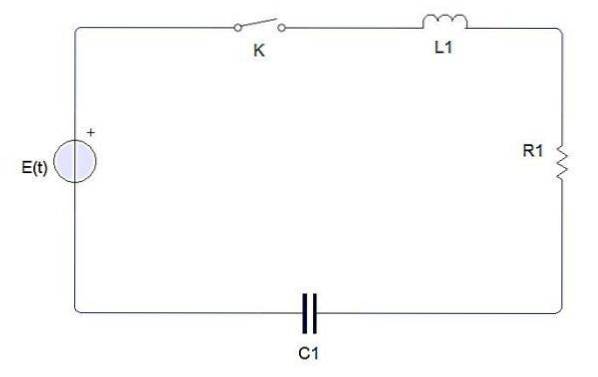
Un comutator, o baterie sau o sursă, un inductor, un rezistor și un condensator. Când comutatorul este închis se produce un curent electric care este notat cu i (t). Sarcina condensatorului este notată cu q (t).
Prin a doua lege a lui Kirchhoff, tensiunea produsă de sursa E către circuitul închis trebuie să fie egală cu suma fiecărei căderi de tensiune.
Curentul electric i (t) este legat de sarcina q (t) de pe condensator de i = dq / dt. Pe de altă parte, căderea de tensiune în fiecare dintre elemente este definită după cum urmează:
Căderea de tensiune pe un rezistor este iR = R (dq / dt)
Căderea de tensiune pe un inductor este L (di / dt) = L (dDouăq / dtDouă)
Căderea de tensiune pe un condensator este q / C
Cu aceste date și aplicând a doua lege a lui Kirchhoff circuitului închis simplu, se obține o ecuație diferențială de ordinul doi care descrie sistemul și ne permite să determinăm valoarea lui q (t).
Exemplu
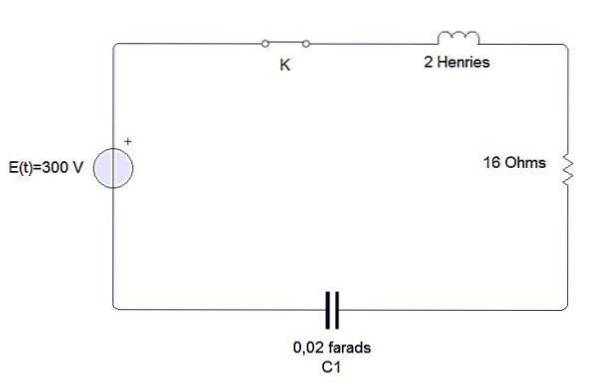
Un inductor, un condensator și un rezistor sunt conectați la o baterie E, așa cum se arată în figură. Inductorul are 2 henries, condensatorul are 0,02 farade și rezistența este de 16 ohmi. La momentul t = 0 circuitul este închis. Găsiți încărcarea și curentul în orice moment t> 0 dacă E = 300 volți.
Avem că ecuația diferențială care descrie acest circuit este următoarea
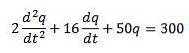
Unde condițiile inițiale sunt q (0) = 0, i (0) = 0 = q '(0).
Aplicând transformata Laplace obținem asta
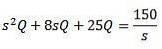
Și rezolvarea pentru Q (t)
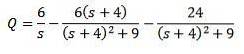
Apoi, aplicând transforma Laplace inversă pe care o avem
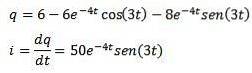
Referințe
- G. Holbrook, J. (1987). Transformarea Laplace pentru inginerii electronici. Limusa.
- Ruiz, L. M. și Hernandez, M. P. (2006). Ecuațiile diferențiale și transformarea Laplace cu aplicațiile. Editorial UPV.
- Simmons, G. F. (1993). Ecuații diferențiale cu aplicații și note istorice. McGraw-Hill.
- Spiegel, M. R. (1991). Laplace se transformă. McGraw-Hill.
- Zill, D. G. și Cullen, M. R. (2008). Ecuații diferențiale cu probleme ale valorii limită. Cengage Learning Editores, S.A.



Nimeni nu a comentat acest articol încă.