
Caracteristici triunghi echilaterale, proprietăți, formule, suprafață
A triunghi echilateral este un poligon cu trei laturi, unde toate sunt egale; adică au aceeași măsură. Pentru această caracteristică i s-a dat numele de echilateral (laturi egale).
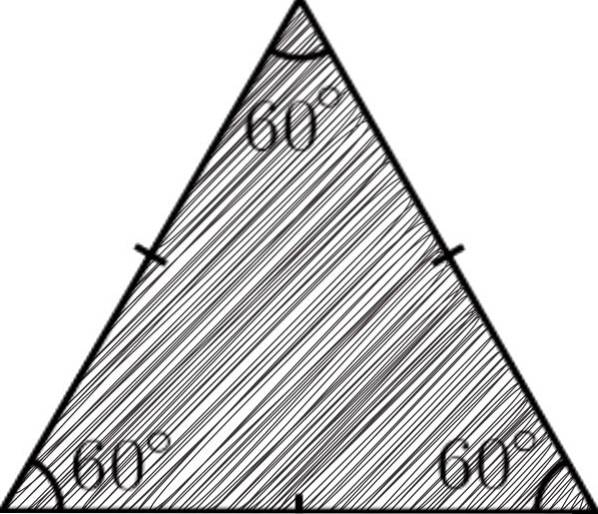
Triunghiurile sunt poligoane considerate cele mai simple în geometrie, deoarece sunt alcătuite din trei laturi, trei unghiuri și trei vârfuri. În cazul triunghiului echilateral, deoarece are laturi egale, implică faptul că cele trei unghiuri ale sale vor fi, de asemenea, egale..
Indice articol
- 1 Caracteristicile triunghiurilor echilaterale
- 1.1 - laturi egale
- 1.2 - Componente
- 2 Proprietăți
- 2.1 Unghiuri interne
- 2.2 Unghiuri externe
- 2.3 Suma laturilor
- 2.4 Părți congruente
- 2.5 Unghiuri congruente
- 3 Cum se calculează perimetrul?
- 4 Cum se calculează înălțimea?
- 5 Cum se calculează laturile?
- 6 Cum se calculează aria?
- 7 Exerciții
- 7.1 - Primul exercițiu
- 7.2 - Al doilea exercițiu
- 7.3 - Al treilea exercițiu
- 8 Referințe
Caracteristicile triunghiurilor echilaterale
- Părți egale
Triunghiurile echilaterale sunt figuri plate și închise, alcătuite din trei segmente de linie. Triunghiurile sunt clasificate după caracteristicile lor, în raport cu laturile și unghiurile lor; echilaterul a fost clasificat folosind măsura laturilor sale ca parametru, deoarece acestea sunt exact aceleași, adică sunt congruente.
Triunghiul echilateral este un caz particular al triunghiului isoscel, deoarece două dintre laturile sale sunt congruente. De aceea, toate triunghiurile echilaterale sunt și ele isoscele, dar nu toate triunghiurile isoscele vor fi echilaterale.
În acest fel, triunghiurile echilaterale au aceleași proprietăți ca și un triunghi isoscel..
Triunghiurile echilaterale pot fi, de asemenea, clasificate după lățimea unghiurilor lor interioare ca un triunghi acut echilateral, care are trei laturi și trei unghiuri interioare cu aceeași măsură. Unghiurile vor fi acute, adică vor fi mai mici de 90sau.
- Componente (editați)
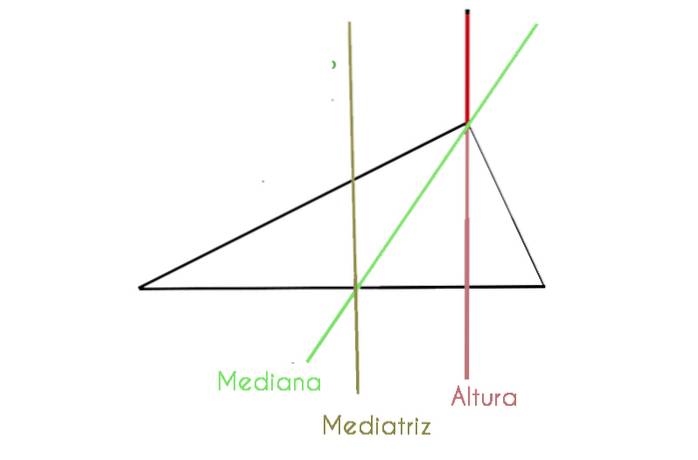
Triunghiurile, în general, au mai multe linii și puncte care îl compun. Sunt folosite pentru a calcula aria, laturile, unghiurile, mediana, bisectoarea, bisectoarea și înălțimea..
- Median: este o linie care începe din punctul de mijloc al unei părți și ajunge la vârful opus. Cele trei mediane converg într-un punct numit baricentr sau centroid..
- Bisector: este o rază care împarte unghiul vârfurilor în două unghiuri de măsură egală, de aceea este cunoscută sub numele de axa de simetrie. Triunghiul echilateral are trei axe de simetrie. În triunghiul echilateral, bisectoarea este trasă de la vârful unui unghi spre latura opusă, tăind-o în punctul său mediu. Acestea se întâlnesc într-un punct numit stimulator.
- Mediatrixul: este un segment perpendicular pe latura triunghiului care își are originea în mijlocul acestuia. Există trei mediatori într-un triunghi și se întâlnesc într-un punct numit circumcentrul.
- Inaltimea: este linia care merge de la vârf la partea opusă și, de asemenea, această linie este perpendiculară pe acea parte. Toate triunghiurile au trei înălțimi care coincid într-un punct numit ortocentru..
În graficul următor vedem un triunghi scalen în care sunt detaliate unele dintre componentele menționate
Bisectoarea, mediana și bisectoarea sunt coincidente
Bisectoarea împarte latura unui triunghi în două părți. În triunghiuri echilaterale acea parte va fi împărțită în două părți exact egale, adică triunghiul va fi împărțit în două triunghiuri dreptunghiulare congruente.
Astfel, bisectoarea trasă din orice unghi al unui triunghi echilateral coincide cu mediana și bisectoarea laturii opuse acelui unghi..
Exemplu:
Următoarea figură arată triunghiul ABC cu un punct mediu D care împarte una dintre laturile sale în două segmente AD și BD.
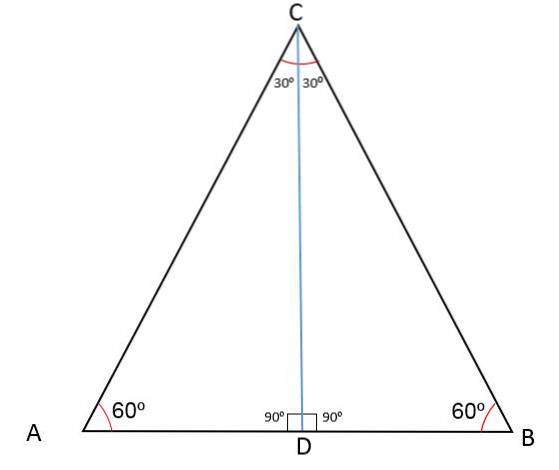
Prin trasarea unei linii de la punctul D la vârful opus, prin definiție se obține CD-ul median, care este relativ la vârful C și latura AB.
Deoarece segmentul CD împarte triunghiul ABC în două triunghiuri egale CDB și CDA, înseamnă că va fi cazul de congruență: latură, unghi, latură și, prin urmare, CD va fi și bisectoarea BCD.
Plotarea segmentului CD împarte unghiul vârfului în două unghiuri egale de 30sau, unghiul vârfului A măsoară încă 60sau iar linia CD formează un unghi de 90sau cu privire la punctul mediu D.
Segmentul CD formează unghiuri care au aceeași măsură pentru triunghiurile ADC și BDC, adică sunt suplimentare în așa fel încât măsura fiecăruia să fie:
Med. (ADB) + Med. (ADC) = 180sau
Două * Med. (ADC) = 180sau
Med. (ADC) = 180sau ÷ 2
Med. (ADC) = 90sau.
Deci, avem că segmentul CD este și bisectoarea laturii AB.
Bisectoarea și înălțimea sunt coincidente
Prin trasarea bisectoarei de la vârful unui unghi până la punctul mediu al părții opuse, împarte triunghiul echilateral în două triunghiuri congruente.
În așa fel încât se formează un unghi de 90sau (dreapta). Aceasta indică faptul că acel segment de linie este total perpendicular pe acea parte și, prin definiție, acea linie ar fi înălțimea.
În acest fel, bisectoarea oricărui unghi al unui triunghi echilateral coincide cu înălțimea relativă la partea opusă a acelui unghi..
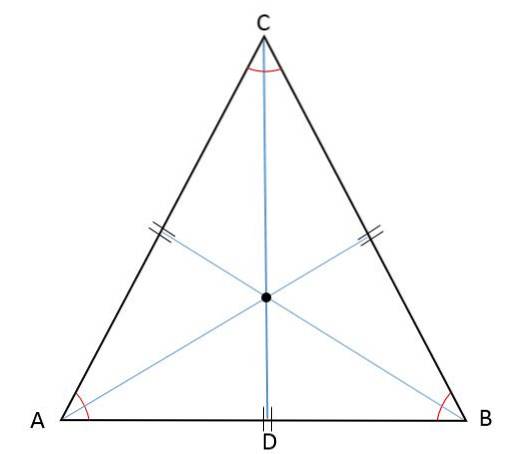
Ortocentrul, baricentrul, incinerul și circumcentrul coincident
Deoarece înălțimea, mediana, bisectoarea și bisectoarea sunt reprezentate de același segment în același timp, într-un triunghi echilateral punctele de întâlnire ale acestor segmente -ortocentrul, bisectoarea, incinerul și circumcentrul- vor fi găsite în același punct:
Proprietăți
Principala proprietate a triunghiurilor echilaterale este că acestea vor fi întotdeauna triunghiuri isoscele, deoarece isoscelele sunt formate din două laturi congruente și echilaterale de trei..
În acest fel, triunghiurile echilaterale au moștenit toate proprietățile triunghiului isoscel:
Unghiuri interne
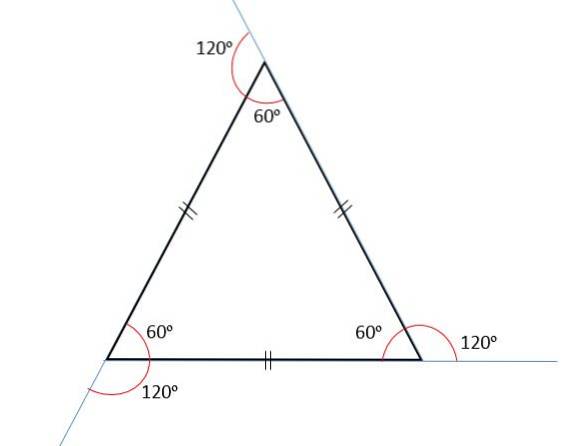
Suma unghiurilor interioare este întotdeauna egală cu 180sau, și întrucât toate unghiurile sale sunt congruente, atunci fiecare dintre acestea va măsura 60sau.
Unghiuri externe
Suma unghiurilor exterioare va fi întotdeauna egală cu 360sau, de aceea fiecare unghi extern va măsura 120sau. Acest lucru se datorează faptului că unghiurile interne și externe sunt suplimentare, adică la adăugarea lor vor fi întotdeauna egale cu 180sau.
Suma laturilor
Suma măsurilor celor două laturi trebuie să fie întotdeauna mai mare decât măsura celei de-a treia părți, adică a + b> c, unde a, b și c sunt măsurile fiecărei părți.
Părți congruente
Triunghiurile echilaterale au toate cele trei laturi cu aceeași măsură sau lungime; adică sunt congruente. Prin urmare, în elementul anterior avem că a = b = c.
Unghiuri congruente
Triunghiurile echilaterale sunt, de asemenea, cunoscute sub numele de triunghiuri echiangulare, deoarece cele trei unghiuri interioare ale acestora sunt congruente între ele. Acest lucru se datorează faptului că toate părțile sale au, de asemenea, aceeași măsurare.
Cum se calculează perimetrul?
Perimetrul unui poligon se calculează prin adăugarea laturilor. Ca și în acest caz, triunghiul echilateral are toate laturile sale cu aceeași măsură, perimetrul său se calculează cu următoarea formulă:
P = 3 * latură.
Cum se calculează înălțimea?
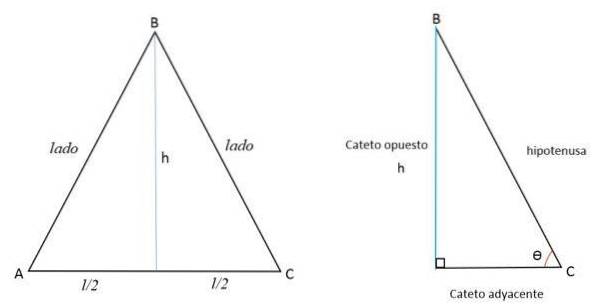
Deoarece înălțimea este linia perpendiculară pe bază, aceasta o împarte în două părți egale extinzându-se la vârful opus. Astfel se formează două triunghiuri drepte egale.
Înălțimea (h) reprezintă piciorul opus (a), jumătate din partea AC față de piciorul adiacent (b), iar latura BC reprezintă hipotenuza (c).
Folosind teorema lui Pitagora, se poate determina valoarea înălțimii:
laDouă + bDouă = cDouă
Unde:
laDouă = înălțime (h).
bDouă = latura b / 2.
cDouă = latura a.
Înlocuind aceste valori în teorema lui Pitagora și rezolvând înălțimea, avem:
hDouă + ( l / Două)Două = lDouă
hDouă + lDouă/ 4 = lDouă
hDouă = lDouă - lDouă/ 4
hDouă = (4*lDouă - lDouă) / 4
hDouă = 3*lDouă /4
√hDouă = √ (3*lDouă /4)

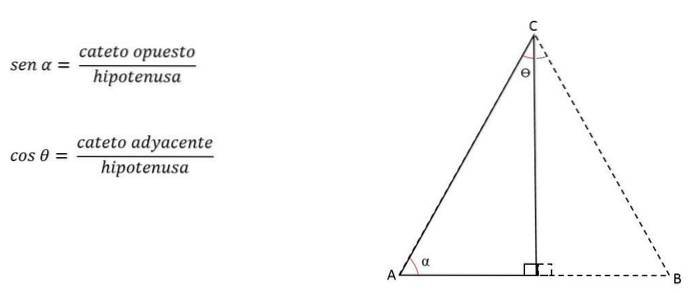
Dacă unghiul format de laturile congruente este cunoscut, înălțimea (reprezentată de un picior) poate fi calculată prin aplicarea raporturilor trigonometrice.
Picioarele sunt numite opuse sau adiacente în funcție de unghiul luat ca referință..
De exemplu, în figura de deasupra piciorului h va fi opus pentru unghiul C, dar adiacent unghiului B:
Astfel, înălțimea poate fi calculată cu:
Cum se calculează laturile?
Există cazuri în care măsurile laturilor triunghiului nu sunt cunoscute, dar înălțimea lor și unghiurile formate la vârfuri.
Pentru a determina aria în aceste cazuri este necesar să se aplice rapoartele trigonometrice.
Cunoscând unghiul unuia dintre vârfurile sale, picioarele sunt identificate și se folosește raportul trigonometric corespunzător:
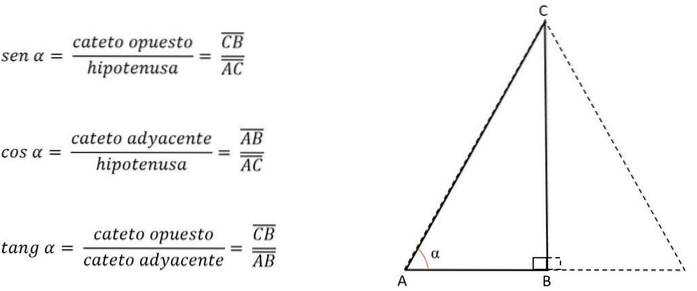
Astfel, piciorul AB va fi opus pentru unghiul C, dar adiacent unghiului A. În funcție de latura sau piciorul corespunzător înălțimii, cealaltă parte este degajată pentru a-și obține valoarea, știind că într-un triunghi echilateral cele trei laturi vor avea întotdeauna aceeași măsurare.
Cum se calculează suprafața?
Aria triunghiurilor este întotdeauna calculată cu aceeași formulă, înmulțind baza de ori înălțimea și împărțind la două:
Suprafață = (b * h) ÷ 2
Știind că înălțimea este dată de formula:

Instruire
- Primul exercițiu
Laturile unui triunghi echilateral ABC sunt fiecare de 20 cm. Calculați înălțimea și aria poligonului respectiv.
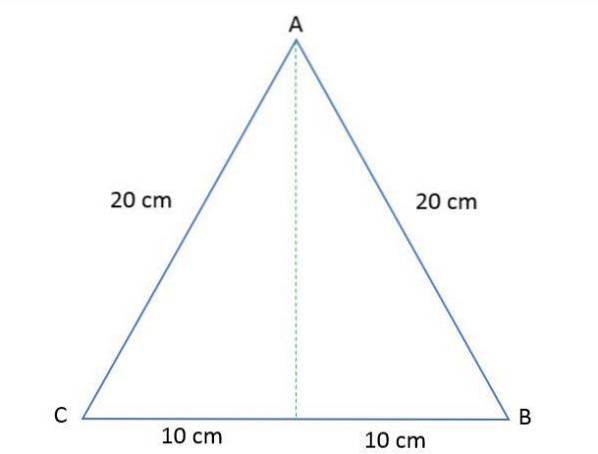
Soluţie
Pentru a determina aria acestui triunghi echilateral, este necesar să se calculeze înălțimea, știind că atunci când îl desenăm, împarte triunghiul în două triunghiuri drepte egale.
În acest fel, teorema lui Pitagora poate fi folosită pentru a o găsi:
laDouă + bDouă = cDouă
Unde:
a = 20/2 = 10 cm.
b = înălțime.
c = 20 cm.
Datele sunt substituite în teoremă:
10Două + bDouă = 20Două
100 cm + bDouă = 400 cm
bDouă = (400 - 100) cm
bDouă = 300cm
b = √300 cm
b = 17,32 cm.
Adică înălțimea triunghiului este egală cu 17,32cm. Acum este posibil să se calculeze aria triunghiului dat prin înlocuirea formulei:
Suprafață = (b * h) ÷ 2
Suprafață = (20 cm * 17,32 cm) ÷ 2
Suprafață = 346,40 cmDouă ÷ 2
Suprafață = 173,20 cmDouă.
O altă modalitate mai simplă de a rezolva exercițiul este prin înlocuirea datelor din formula directă a zonei, unde valoarea înălțimii se găsește și implicit:

- Al doilea exercițiu
Florile vor fi plantate pe o bucată de pământ care are forma unui triunghi echilateral. Dacă perimetrul acelui teren este egal cu 450 m, calculați numărul de metri pătrați pe care îl vor ocupa florile.
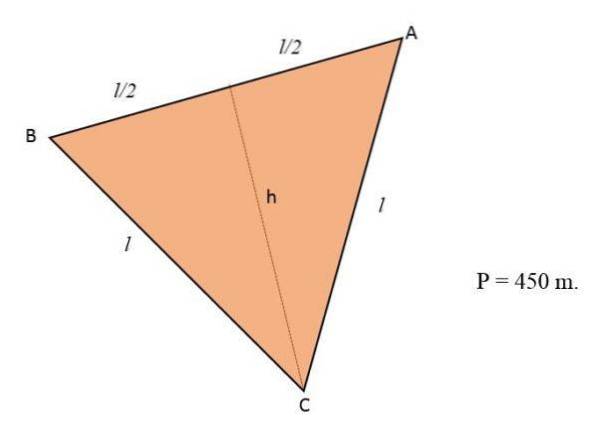
Soluţie
Știind că perimetrul unui triunghi corespunde sumei celor trei laturi ale sale și întrucât terenul are forma unui triunghi echilateral, cele trei laturi ale acestuia vor avea aceeași măsură sau lungime:
P = lat + lat + lat = 3 * l
3 * l = 450 m.
l = 450 m ÷ 3
l = 150 m.
Acum este necesar doar să se calculeze înălțimea acelui triunghi.
Înălțimea împarte triunghiul în două triunghiuri drepte congruente, unde un picior reprezintă înălțimea și cealaltă jumătate a bazei. Prin teorema lui Pitagora, înălțimea poate fi determinată:
laDouă + bDouă = cDouă
Unde:
la = 150 m ÷ 2 = 75 m.
c = 150 m.
b = înălțime
Datele sunt substituite în teoremă:
(75 m)Două + bDouă = (150 m)Două
5.625 m + bDouă = 22.500 m
bDouă = 22.500 m - 5.625 m
bDouă = 16.875 m
b = √16.875 m
b = 129,90 m.
Astfel zona pe care o vor ocupa florile va fi:
Suprafața = b * h ÷ 2
Suprafață = (150 m * 129,9 m) ÷ 2
Suprafață = (19.485 mDouă) ÷ 2
Suprafață = 9.742,5 mDouă
- Al treilea exercițiu
Triunghiul echilateral ABC este împărțit de un segment de linie care merge de la vârful său C la punctul mediu D, situat pe partea opusă (AB). Acest segment măsoară 62 de metri. Calculați aria și perimetrul acelui triunghi echilateral.
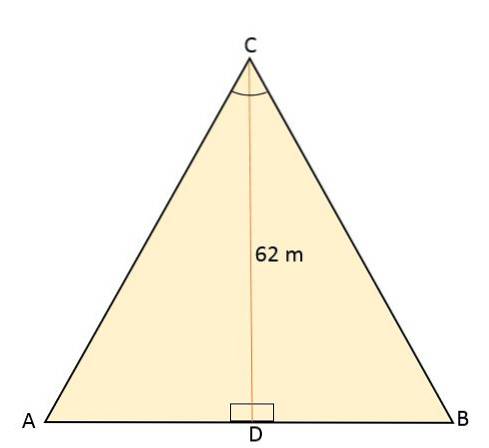
Soluţie
Știind că triunghiul echilateral este împărțit printr-un segment de linie care corespunde înălțimii, formând astfel două triunghiuri drepte congruente, acesta la rândul său împarte unghiul vârfului C în două unghiuri cu aceeași măsură, 30sau fiecare.
Înălțimea formează un unghi de 90sau în raport cu segmentul AB, iar unghiul vârfului A va măsura apoi 60sau.
Apoi, folosind unghiul 30 ca referințăsau, înălțimea CD este setată ca piciorul adiacent unghiului și BC ca hipotenuză.
Din aceste date, se poate determina valoarea uneia dintre laturile triunghiului, utilizând raporturile trigonometrice:
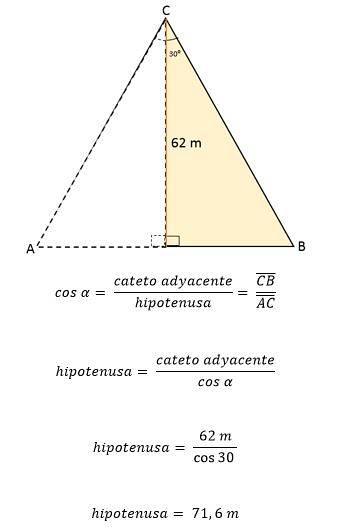
Deoarece în triunghiul echilateral toate laturile au exact aceeași măsură sau lungime, înseamnă că fiecare latură a triunghiului echilateral ABC este egală cu 71,6 metri. Știind asta, este posibil să se determine aria sa:
Suprafața = b * h ÷ 2
Suprafață = (71,6 m * 62 m) ÷ 2
Suprafață = 4.438,6 mDouă ÷ 2
Suprafață = 2.219,3 mDouă
Perimetrul este dat de suma celor trei laturi ale sale:
P = lat + lat + lat = 3 * l
P = 3*l
P = 3 * 71,6 m
P = 214,8 m.
Referințe
- Álvaro Rendón, A. R. (2004). Desen tehnic: carte de activitate.
- Arthur Goodman, L. H. (1996). Algebră și trigonometrie cu geometrie analitică. Pearson Education.
- Baldor, A. (1941). Algebră. Havana: Cultură.
- BARBOSA, J. L. (2006). Geometria plană euclidiană. SBM. Rio de Janeiro, .
- Coxford, A. (1971). Geometrie O abordare de transformare. SUA: Laidlaw Brothers.
- Euclid, R. P. (1886). Elementele de geometrie ale lui Euclid.
- Héctor Trejo, J. S. (2006). Geometrie și trigonometrie.
- León Fernández, G. S. (2007). Geometrie integrată. Institutul Tehnologic Metropolitan.
- Sullivan, J. (2006). Algebră și trigonometrie. Pearson Education.



Nimeni nu a comentat acest articol încă.