Caracteristici și proprietăți vectoriale, elemente, tipuri, exemple

vector Sunt entități matematice care au o magnitudine -pozițională, în general însoțite de o unitate de măsură, precum și direcție și sens. Astfel de caracteristici sunt foarte potrivite pentru a descrie mărimi fizice precum viteza, forța, accelerația și multe altele..

Cu vectori este posibil să se efectueze operații precum adunarea, scăderea și produsele. Diviziunea nu este definită pentru vectori și, în ceea ce privește produsul, există trei clase pe care le vom descrie mai târziu: produs punct sau punct, produs vector sau cruce și produsul unui scalar cu un vector.

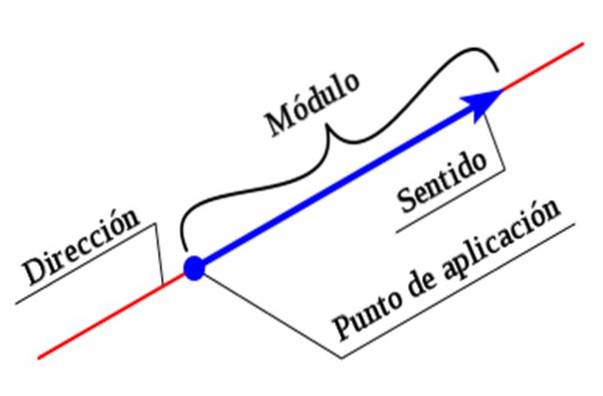
Pentru a descrie pe deplin un vector, este necesar să se indice toate caracteristicile acestuia. Mărimea sau modulul este o valoare numerică însoțită de o unitate, în timp ce direcția și direcția sunt stabilite cu ajutorul unui sistem de coordonate.

Să vedem un exemplu: să presupunem că un avion zboară dintr-un oraș în altul cu o rată de 850 km / h în direcția NE. Aici avem un vector complet specificat, deoarece magnitudinea este disponibilă: 850 km / h, în timp ce direcția și sensul sunt NE.

Vectorii sunt de obicei reprezentați grafic prin segmente de linie orientate, a căror lungime este proporțională cu magnitudinea.

În timp ce pentru a specifica direcția și sensul este necesară o linie de referință, care este de obicei axa orizontală, deși nordul poate fi luat și ca referință, așa este cazul vitezei planului:

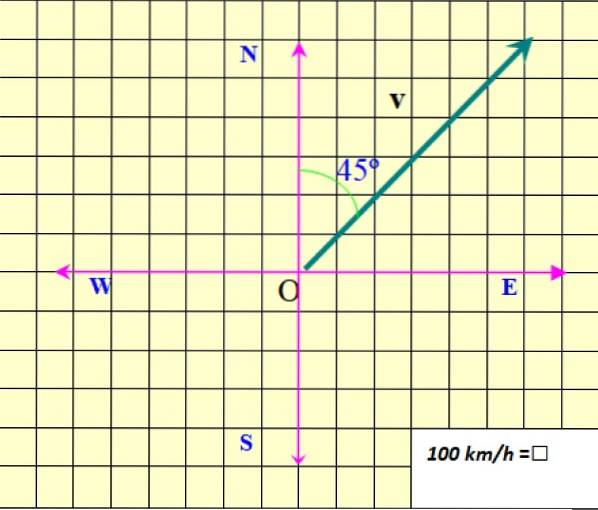
Figura arată vectorul vitezei planului, care este notat ca v pe îndrăzneţ, pentru a o distinge de o cantitate scalară, care necesită doar o valoare numerică și trebuie specificată o anumită unitate.

Indice articol

• 1 Elemente ale unui vector
  • 1.1 Componente dreptunghiulare ale unui vector
• 2 tipuri
  • 2.1 Vectorii unitari ortogonali
• 3 Suma de vectori
  • 3.1 Proprietățile adunării vectoriale
• 4 Exemple de vectori
• 5 Alte operații între vectori
  • 5.1 Produsul unui scalar și a unui vector
  • 5.2 Produs scalar sau produs punct între vectori
  • 5.3 Produs încrucișat sau produs încrucișat între vectori
• 6 exerciții rezolvate
  • 6.1 - Exercițiul 1
  • 6.2 - Exercițiul 2
• 7 Referințe

Elemente ale unui vector

După cum am spus, elementele vectorului sunt:

-Magnitudine sau modul, uneori numit și valoare absolută sau normă a vectorului.

-Direcţie

-Sens

În exemplul din figura 2, modulul v Este de 850 km / h. Modulul este notat ca v fără aldine sau ca |v|, unde barele reprezintă valoarea absolută.

Adresa de v este specificat cu privire la Nord. În acest caz, se află la 45º nord de est (45º NE). În cele din urmă, vârful săgeții informează despre direcția v.

În acest exemplu, originea vectorului a fost trasă coincizând cu originea O a sistemului de coordonate, aceasta este cunoscută sub numele de vector legat. Pe de altă parte, dacă originea vectorului nu coincide cu cea a sistemului de referință, se spune că este a vector gratuit.

Trebuie remarcat faptul că, pentru a specifica pe deplin vectorul, trebuie menționate aceste trei elemente, altfel descrierea vectorului ar fi incompletă.

Componente dreptunghiulare ale unui vector

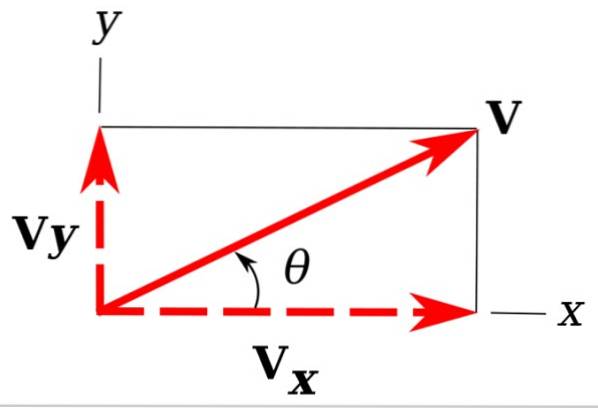
În imagine avem înapoi vectorul nostru de exemplu v, adică în avion X y.

Este ușor de văzut că proiecțiile lui v pe axele coordonatelor x și y determină un triunghi dreptunghiular. Aceste proiecții sunt v_Da Da v_X și se numesc componente dreptunghiulare ale v.

O modalitate de a denota v prin componentele sale dreptunghiulare este așa: v = X, v_Da>. Aceste paranteze sunt folosite în loc de paranteze pentru a sublinia faptul că este un vector și nu un punct, deoarece în acest caz ar fi utilizate paranteze.

Dacă vectorul este în spațiu tridimensional, este necesară încă o componentă, astfel încât:

v = X, v_Da, v_z>

Cunoscând componentele dreptunghiulare, se calculează magnitudinea vectorului, echivalent cu găsirea ipotenuzei triunghiului dreptunghic ale cărui picioare sunt v_X Da v_Da,. Prin intermediul teoremei pitagoreice rezultă că:

|v|^Două = (v_X)^Două +  (v_Da)^Două

Forma polară a unui vector

Când se cunoaște magnitudinea vectorului |v| și unghiul θ pe care îl formează aceasta cu axa de referință, în general axa orizontală, se specifică și vectorul. Se spune apoi că vectorul este exprimat în formă polară.

Componentele dreptunghiulare în acest caz sunt ușor calculate:

v_X = |v| .cos θ

v_Da = |v| .sen θ

Conform celor de mai sus, componentele dreptunghiulare ale vectorului viteză v a avionului ar fi:

v_X = 850. cos 45º km / h = 601,04 km / h

v_Da = 850. fără 45º km / h = 601,04 km / h

Tipuri

Există mai multe tipuri de vectori. Există vectori de viteză, poziție, deplasare, forță, câmp electric, impuls și multe altele. După cum am spus deja, în fizică există un număr mare de mărimi vectoriale.

În ceea ce privește vectorii care au anumite caracteristici, putem menționa următoarele tipuri de vectori:

-Nul: sunt vectori a căror magnitudine este 0 și care sunt notați ca 0. Amintiți-vă că litera aldinată simbolizează cele trei caracteristici fundamentale ale unui vector, în timp ce litera normală reprezintă doar modulul.

De exemplu, pe un corp în echilibru static, suma forțelor trebuie să fie un vector nul.

-Liber și legat: vectorii liberi sunt cei ale căror puncte de origine și de sosire sunt orice pereche de puncte din plan sau din spațiu, spre deosebire de vectorii legați, a căror origine coincide cu cea a sistemului de referință folosit pentru a le descrie.

Cuplul sau momentul produs de câteva forțe este un bun exemplu de vector liber, deoarece cuplul nu se aplică în niciun punct anume.

-Lentile de echipă: sunt doi vectori liberi care împărtășesc caracteristici identice. Prin urmare, au o magnitudine, o direcție și un sens egale.

-Coplanar sau coplanar: vectori care aparțin aceluiași plan.

-Opusuri: vectori cu magnitudine și direcție egale, dar direcții opuse. Vectorul opus unui vector v este vectorul -v iar suma ambelor este vectorul nul: v + (-v) = 0.

-Concurente: vectori ale căror linii de acțiune trec prin același punct.

-Glisoare: sunt acei vectori al căror punct de aplicare poate aluneca de-a lungul unei anumite linii.

-Coliniar: vectori care sunt localizați pe aceeași linie.

-Unitar: acei vectori al căror modul este 1.

Vectorii unitari ortogonali

Există un tip foarte util de vector în fizică numit vector unitate ortogonală. Vectorul de unitate ortogonală are un modul egal cu 1 și unitățile pot fi oricare, de exemplu cele de viteză, poziție, forță sau altele.

Există un set de vectori speciali care ajută la reprezentarea cu ușurință a altor vectori și la efectuarea operațiilor asupra lor: sunt vectori de unitate ortogonali eu, j Da k, unitare și perpendiculare una pe cealaltă.

În două dimensiuni, acești vectori sunt direcționați de-a lungul direcției pozitive a ambelor axe X ca al axei Da. Și în trei dimensiuni se adaugă un vector unitar în direcția axei z pozitiv. Acestea sunt reprezentate după cum urmează:

eu = <1, 0,0>

j = < 0,1,0>

k = <0,0,1>

Un vector poate fi reprezentat de vectorii unitari eu, j Da k după cum urmează:

v = v_X eu + v_Da j + v_z k

De exemplu vectorul viteză v din exemplele de mai sus pot fi scrise ca:

v = 601,04 eu + 601.04 j km / h

Componenta din k nu este necesar, deoarece acest vector este în plan.

Adăugare vectorială

Suma vectorilor apare foarte frecvent în diverse situații, de exemplu atunci când doriți să găsiți forța rezultată asupra unui obiect care este afectat de diferite forțe. Pentru început, să presupunem că avem doi vectori liberi sau Da v în plan, așa cum se arată în următoarea figură din stânga:

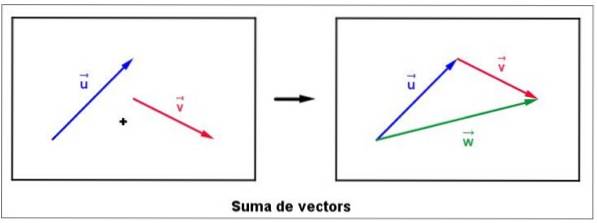
Este mutat imediat cu atenție la vector v, fără a-și modifica magnitudinea, direcția sau simțul, astfel încât originea sa să coincidă cu sfârșitul anului sau.

Se numește vectorul sumă w și se trage începând de la u terminându-se cu v, conform cifrei potrivite. Este important să rețineți că amploarea vectorului w nu este neapărat suma mărimilor lui v Da sau.

Dacă vă gândiți cu atenție la acest lucru, singura dată când magnitudinea vectorului rezultat este suma mărimilor adunărilor, este atunci când ambele adunări sunt în aceeași direcție și au același sens..

Și ce se întâmplă dacă vectorii nu sunt liberi? De asemenea, este foarte ușor să le adăugați. Modalitatea de a face acest lucru este adăugarea componentului la componentă sau metoda analitică.

De exemplu, să luăm în considerare vectorii din figura următoare, primul lucru este să-i exprimăm într-unul din modurile carteziene explicate anterior:

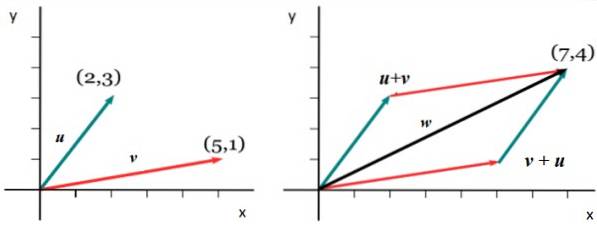
v = <5,1>

sau = <2,3>

Pentru a introduce componenta X a vectorului sumă w, componentele respective sunt adăugate în X din v Da sau: w_X = 5 + 2 = 7. Și pentru a obține w_Da se urmează o procedură analogă: w_Da = 1 + 3. Prin urmare:

sau = <7,4>

Proprietățile adăugării vectoriale

-Suma a doi sau mai mulți vectori are ca rezultat un alt vector.

-Este comutativ, ordinea suplimentelor nu modifică suma, în așa fel încât:

sau + v = v + sau

-Elementul neutru al sumei de vectori este vectorul nul: v + 0 = v

-Scăderea a doi vectori este definită ca suma opusului: v - u = v + (-sau)

Exemple de vectori

După cum am spus, există numeroase cantități de vectori în fizică. Printre cele mai cunoscute sunt:

-Poziţie

-Deplasare

-Viteza medie și viteza instantanee

-Accelerare

-Forta

-Cantitatea de mișcare

-Cuplul sau momentul unei forțe

-Impuls

-câmp electric

-Camp magnetic

-Moment magnetic

Pe de altă parte, nu sunt vectori, ci scalari:

-Vreme

-Masa

-Temperatura

-Volum

-Densitate

-Munca mecanica

-Energie

-Fierbinte

-Putere

-Voltaj

-Curent electric

Alte operații între vectori

În plus față de adunarea și scăderea vectorilor, există alte trei operații foarte importante între vectori, deoarece acestea dau naștere la noi mărimi fizice foarte importante:

-Produs al unui scalar și al unui vector.

-Produsul punct sau produsul punct între vectori

-Și produsul încrucișat sau vectorial între doi vectori.

Produs al unui scalar și al unui vector

Luați în considerare a doua lege a lui Newton, care afirmă că forța F și accelerație la sunt proporționale. Constanta proporționalității este masa m obiectului, deci:

F = m.la

Masa este un scalar; forța și accelerația sunt vectori. Deoarece forța se obține înmulțind masa cu accelerația, aceasta este rezultatul produsului unui scalar și al unui vector.

Acest tip de produs are ca rezultat întotdeauna un vector. Iată un alt exemplu: cantitatea de mișcare. Fi P vectorul de impuls, v vectorul vitezei și ca întotdeauna, m este masa:

P = m.v

Produs punct sau produs punct între vectori

Am plasat lucrările mecanice pe lista mărimilor care nu sunt vectori. Cu toate acestea, munca în fizică este rezultatul unei operații între vectori numiți produs scalar, produs interior sau produs punct..

Să fie vectorii v Da sau, produsul punct sau scalarul dintre ele este definit ca:

v∙sau = |v| ∙ |sau | .cos θ

Unde θ este unghiul dintre cele două. Din ecuația prezentată rezultă imediat că rezultatul produsului punct este un scalar și că, dacă ambii vectori sunt perpendiculari, produsul lor scalar este 0.

Înapoi la lucrările mecanice W, acesta este produsul scalar dintre vectorul forței F și vectorul de deplasare ℓ.

W = F∙ℓ                  

Când vectorii sunt disponibili în ceea ce privește componentele lor, produsul punct este, de asemenea, foarte ușor de calculat. da v = X, v_Da, v_z > Da sau = X, sau_Da, sau_z >, produsul punct între cele două este:

v∙sau = v_X sau_X + v_Da sau_Da + v_z sau_z

Produsul punct între vectori este comutativ, prin urmare:

v∙sau = sau∙v

Produs încrucișat sau produs vectorial între vectori

da v și u sunt cei doi exemple de vectori ai noștri, produsul vector este definit ca:

v X sau = w

Urmează imediat că produsul încrucișat are ca rezultat un vector, al cărui modul este definit ca:

|v X tu | = | v | . | u |. sen θ

Unde θ este unghiul dintre vectori.

Prin urmare, produsul încrucișat nu este comutativ v X u ≠ u X v. De fapt v X u = - (u X v).

Dacă cei doi vectori de exemplu sunt exprimați în termeni de vectori unitari, calculul produsului vector este mai ușor:

v = v_X eu + v_Da j + v_z k

sau = u_X eu + sau_Da j + sau_z k

Încrucișați produsele între vectori unitari

Produsul încrucișat între vectori unitari identici este zero, deoarece unghiul dintre ei este 0º. Dar între diferiți vectori unitari, unghiul dintre ei este de 90º și sin 90º = 1.

Următoarea diagramă vă ajută să găsiți aceste produse. În direcția săgeții are o direcție pozitivă și în direcția opusă are o direcție negativă:

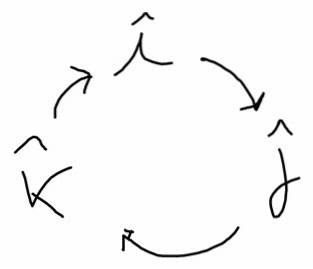
eu X j = k, j X k = i; k X eu = j; j X i = -k; k X j = -i; eu X k = -j

Aplicând proprietatea distributivă, care este încă valabilă pentru produsele dintre vectori plus proprietățile vectorilor unitari, avem:

v X sau = (v_X eu + v_Da j + v_z k) x (u_X eu + sau_Da j + sau_z k) =  

= (v_Dasau_z - v_zsau_Da )eu + (v_zsau_X - v_Xsau_z )j + (v_Xsau_Da - v_Dasau_X )k

Exerciții rezolvate

- Exercitiul 1

Având în vedere vectorii:

v = -5 eu + 4j + 1 k

sau = 2 eu -3 j + 7k

Care ar trebui să fie vectorul w astfel încât suma v + sau + w se pare 6 eu +8 j -10k?

Soluţie

-5 eu + 4j + 1 k

Două eu -3 j + 7k

 w_X eu + w_Da j + w_z k  +

--

6eu + 8 j -10 k

Prin urmare, trebuie să se îndeplinească faptul că:

-5 +2 + w_X = 6 → w_X = 9

4-3 + w_Da = 8 → w_Da = 7

1 + 7 + w_z = -10 → w_z = -18

Raspunsul este: w = 9 eu +7 j - 18k

- Exercițiul 2

Care este unghiul dintre vectori v Da sau din exercițiul 1?

Soluţie

Vom folosi produsul dot. Din definiția pe care o avem:

cos θ = v∙sau / |v| ∙ |sau|

v∙sau= -10 -12 + 7 = -15

|v| = √ (-5)^Două +4^Două +1^Două= √42 = 6,48

|sau| = √2^Două +(-3)^Două +7^Două= √62 = 7,87

Înlocuind aceste valori:

cos θ = -15 / 6,48 x 7,87 = -0,2941 → θ = 107,1 º

Referințe

1. Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 1. Cinematica. Editat de Douglas Figueroa (USB).
2. Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
3. Rex, A. 2011. Fundamentele fizicii. Pearson.
4. Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1.
5. Serway, R., Jewett, J. 2008. Fizica pentru știință și inginerie. Volumul 1. 7. Ed. Cengage Learning.