Calculul vectorului de echilibrare, exemple, exerciții

vector de echilibrare Este cel care se opune vectorului rezultat și, prin urmare, este capabil să echilibreze un sistem, deoarece are aceeași magnitudine și aceeași direcție, dar direcția opusă acestui.

În multe ocazii, vectorul de echilibrare se referă la un vector de forță. Pentru a calcula forța de echilibrare, găsiți mai întâi forța rezultată, așa cum se arată în figura următoare:

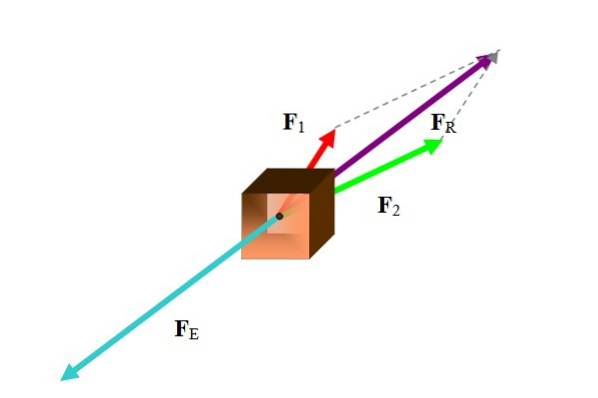
Există diferite metode de realizare a acestei sarcini, în funcție de datele disponibile. Deoarece forțele sunt vectori, rezultanta este suma vectorială a forțelor participante:

F_R = F₁ + F_Două + F₃ +  ... .

Printre metodele care trebuie utilizate se numără metode grafice precum poligonale, paralelograme și metode analitice precum descompunerea forțelor în componentele lor carteziene. În exemplu, figura a folosit metoda paralelogramului.

Odată ce forța rezultată a fost găsită, forța de echilibrare este tocmai vectorul opus.

da F_ȘI este forța de echilibrare, atunci este satisfăcut că F_ȘI aplicat la un moment dat, garantează echilibrul translațional al sistemului. Dacă este o singură particulă, nu se va mișca (sau poate cu viteză constantă), dar dacă este un obiect extins, va avea în continuare capacitatea de a se roti:

F_R + F_ȘI = 0

Indice articol

• 1 Exemple
  • 1.1 Tabel de forțe
• 2 exerciții rezolvate
  • 2.1 -Exercițiunea 1
  • 2.2 -Exerciția 2
• 3 Referințe

Exemple

Forțele de echilibrare sunt prezente peste tot. Noi înșine suntem echilibrați de forța pe care o exercită scaunul pentru a compensa greutatea. Obiectele aflate în repaus: cărți, mobilier, plafoniere și un număr mare de mecanisme, sunt continuu echilibrate de forțe.

De exemplu, o carte în repaus pe o masă este echilibrată de forța normală pe care o exercită asupra cărții, împiedicând-o să cadă. La fel se întâmplă cu lanțul sau cablul care ține lampa atârnată de tavan într-o cameră. Cablurile care dețin o sarcină își distribuie greutatea prin tensiunea din ele.

Într-un fluid, unele obiecte sunt capabile să plutească și să rămână în repaus, deoarece greutatea lor este echilibrată de o forță ascendentă exercitată de lichid, numită Apăsați.

Diferite mecanisme trebuie echilibrate cunoscând vectorul forței de echilibrare, cum ar fi bare, grinzi și coloane.

Atunci când utilizați o cântare, este necesar să echilibrați cumva greutatea obiectului cu o forță echivalentă, fie prin adăugarea de greutăți, fie prin intermediul arcurilor..

Masa de forță

Tabelul forțelor este utilizat în laborator pentru a determina forța de echilibrare. Se compune dintr-o platformă circulară, din care aveți vedere de sus în figură și care are un raportor pentru măsurarea unghiurilor.

Pe marginile mesei sunt scripete prin care trec frânghii care țin greutăți și care converg într-un inel care este în centru.

De exemplu, sunt suspendate două greutăți. Tensiunile generate în corzi de aceste greutăți sunt trasate în roșu și albastru în figura 2. O a treia greutate în verde poate echilibra forța rezultată a celorlalte două și menține sistemul în echilibru..

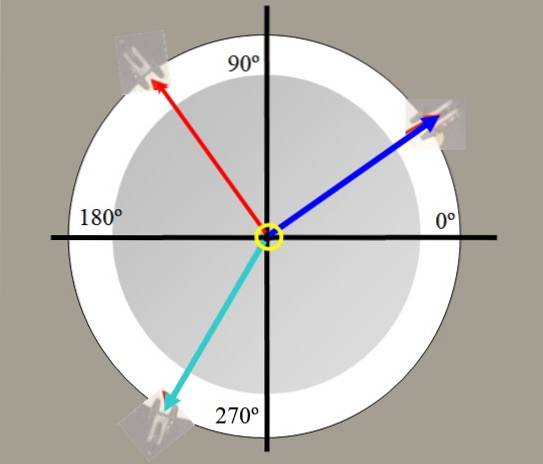
Cu tabelul de forțe este posibil să se verifice caracterul vectorial al forțelor, să se descompună forțele, să se găsească forța de echilibrare și să se verifice teorema lui Lamy:

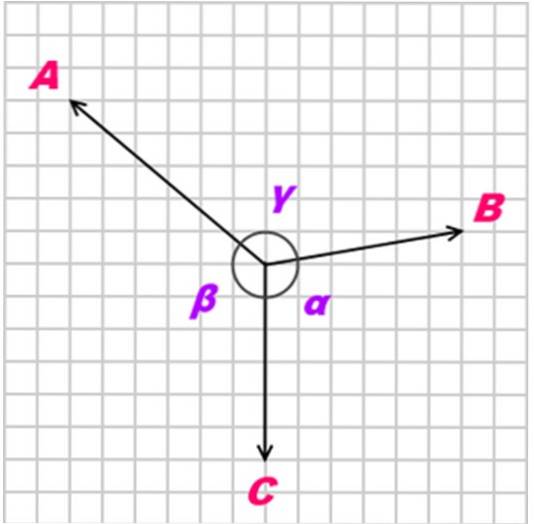
În cazul în care un corpul este în echilibru datorită a trei forțe coplanare, simultane și necoliniare (nu paralele), numite LA, B Da C, relația dintre aceste forțe este următoarea:

A / sin α = B / sin β = C / sin γ

Exerciții rezolvate

-Exercitiul 1

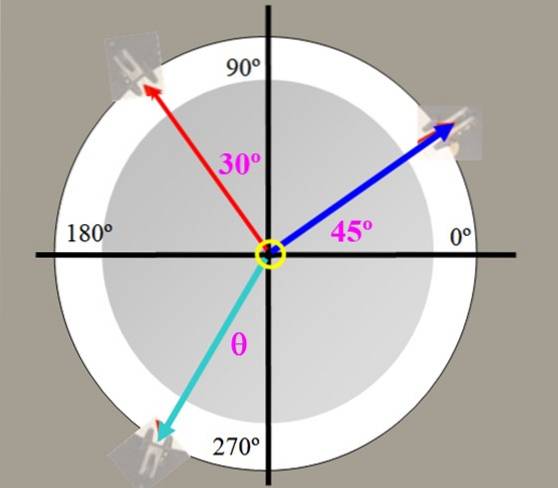
Masele de 225 g (tensiune albastră) și 150 g (tensiune roșie) sunt agățate pe masa forței din figura 2, cu unghiurile prezentate. Găsiți valoarea forței de echilibrare și unghiul pe care îl face cu axa verticală.

Soluţie

Problema poate fi rezolvată cu greutățile exprimate în grame (forțe). Fie P₁ = 150 grame și P_Două = 225 grame, componentele respective ale fiecăruia sunt:

P_1x = 225. cos 45 ° g = 159,10 g; P_1y = 225. cos 45º g = 159.10 g

P_2x = -150. sin 30 g = -75,00 g; P_{2 și} = 150. cos 30º g = 129,90 g

Greutatea rezultată P_R se găsește prin adăugarea algebrică a componentelor:

P_Rx = 159,10 - 75,00 g = 84,10 g

P_Ry = 159,10 + 129,90 g = 289,00 g

Greutatea de echilibrare P_ȘI este vectorul opus P_R:

P_Fost = -84,10 g

P_Hei = -289,00 g

Mărimea greutății de echilibrare este calculată prin:

P_ȘI = (P_Fost^Două + P_Hei^Două)^1/2 = ((-84,10)^Două + (-289,00)^Două)^1/2 g = 301 g

Unghiul θ din figură este:

θ = arctg (-84.10 / -289.00) = 16.2º în raport cu axa Da negativ.

-Exercițiul 2

Găsiți vectorul de echilibrare al sistemului prezentat în figură, știind că fiecare pătrat măsoară 10 m pe o parte.

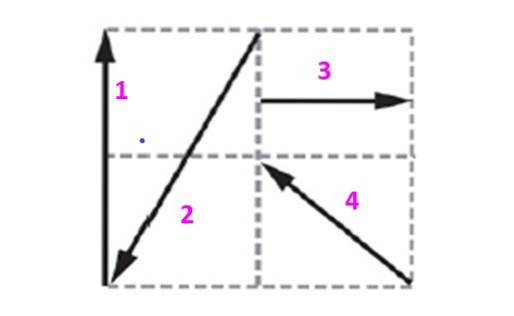
Soluţie

Vectorii conținuți în această grilă vor fi exprimați în termeni de unitate și vectori ortogonali eu Da j care determină planul. Vectorul 1, care va fi notat ca v₁ are magnitudinea de 20 m și este îndreptată vertical în sus. Poate fi exprimat ca:

v₁ = 0 eu +douăzeci j m

Din desen se poate observa că vectorul 2 este:

v_Două = -10 eu - douăzeci j m

Vectorul 3 este orizontal și arată în direcția pozitivă:

v₃ = 10 eu + 0 j  m

În cele din urmă, vectorul 4 este înclinat la 45 °, deoarece este diagonala pătratului, prin urmare componentele sale măsoară la fel:

v₄ = -10 eu + 10 j m

Rețineți că semnele indică spre ce parte a axei sunt componentele: deasupra și spre dreapta au un semn +, în timp ce dedesubt și la stânga au un semn -.

Vectorul rezultat se obține prin adăugarea componentei la componentă:

v_R = -10 eu + 10 j m

Atunci vectorul de echilibrare al sistemului este:

v_ȘI = 10 eu - 10 j m

Referințe

1. Beardon, T. 2011. O introducere la vectori. Adus de la: nrich.maths.org.
2. Bedford, 2000. A. Mecanica inginerească: statică. Addison Wesley. 38-52.
3. Figueroa, D. Seria: Fizică pentru științe și inginerie. Volumul 1. Cinematică 31-68.
4. Fizic. Modulul 8: vectori. Recuperat de la: frtl.utn.edu.ar
5. Hibbeler, R. 2006. Mecanica pentru ingineri. Static. Ediția a 6-a. Compania Editura Continental. 15-53.
6. Calculator de adăugare de vectori. Recuperat de la: 1728.org
7. Vectori. Recuperat de pe: wikibooks.org