
Calcul vectorial rezultat, exemple, exerciții
vector rezultat este cea obținută prin intermediul unei operații cu vectori al căror rezultat este și un vector. În mod normal, această operație este suma a doi sau mai mulți vectori, prin intermediul cărora se obține un vector al cărui efect este echivalent.
În acest fel se obțin vectori precum viteza, accelerația sau forța rezultată. De exemplu, atunci când mai multe forțe acționează asupra unui corp F1, FDouă, F3,…. suma vectorială a tuturor acestor forțe este echivalentă cu forța netă (rezultanta), care se exprimă matematic după cum urmează:
F1 + FDouă + F3 +... = FR sau FN

Vectorul rezultat, indiferent dacă este vorba de forțe sau orice altă magnitudine vectorială, se găsește prin aplicarea regulilor de adunare vectorială. Deoarece vectorii au direcție și sens pe lângă valoarea numerică, nu este suficient să adăugați modulele pentru a avea vectorul rezultat.
Acest lucru este adevărat numai în cazul în care vectorii implicați sunt în aceeași direcție (vezi exemple). În caz contrar, este necesar să se utilizeze metode de sumă vectorială, care, în funcție de caz, pot fi geometrice sau analitice..
Indice articol
- 1 Exemple
- 1.1 Metode geometrice pentru a adăuga doi vectori
- 2 Exerciții
- 2.1 -Exercițiunea 1
- 2.2 Exercițiul 2
- 3 Referințe
Exemple
Metodele geometrice pentru a găsi vectorul rezultat sunt metoda poligonală și metoda paralelogramului.
În ceea ce privește metodele analitice, există metoda componentă, prin care poate fi găsit vectorul rezultat din orice sistem de vectori, cu condiția să avem componentele sale carteziene..
Metode geometrice pentru a adăuga doi vectori
Să presupunem că vectorii sau Da v (Le denotăm cu bold pentru a le distinge de scalare). În figura 2a) le avem situate pe plan. În figura 2 b) a fost transferat la vectorul v în așa fel încât originea sa să coincidă cu sfârșitul lui sau. Vectorul rezultat merge de la originea primului (sau) până la vârful ultimului (v):
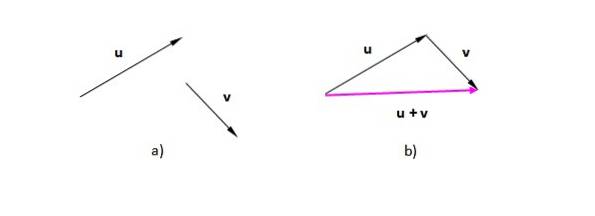
Figura rezultată în acest caz este un triunghi (un triunghi este un poligon cu 3 fețe). Dacă avem doi vectori în aceeași direcție, procedura este aceeași: așezați unul dintre vectori după celălalt și desenați unul care merge de la originea sau coada primului până la vârful sau sfârșitul ultimului.
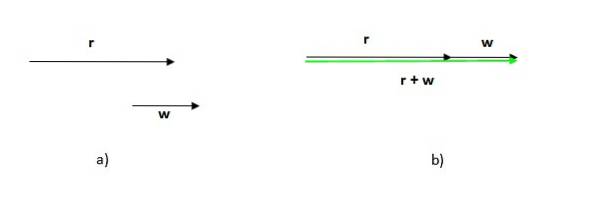
Rețineți că ordinea în care se face această procedură nu contează, deoarece suma vectorilor este comutativă.
De asemenea, rețineți că în acest caz modul (lungimea sau dimensiunea) vectorului rezultat este suma modulelor vectorilor adăugați, spre deosebire de cazul anterior, în care modulul vectorului rezultat este mai mic decât suma modulelor participanților.
Metoda paralelogramelor
Această metodă este foarte potrivită atunci când trebuie să adăugați doi vectori ale căror puncte de origine coincid, să zicem, cu originea unui sistem de coordonate x-y. Să presupunem că acesta este cazul vectorilor noștri sau Da v (figura 3a):
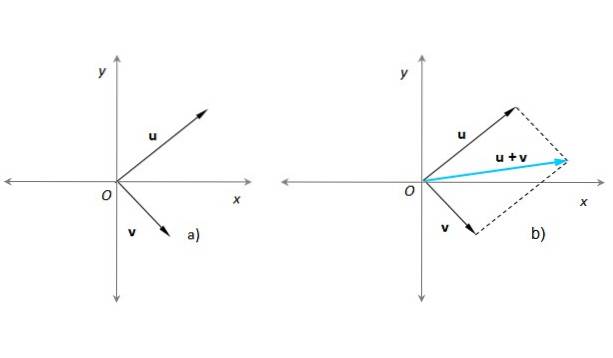
În figura 3b) a fost construit un paralelogram cu ajutorul liniilor punctate paralele cu sau deja v. Vectorul rezultat își are originea la O și capătul său la punctul în care se intersectează liniile punctate. Această procedură este complet echivalentă cu cea descrisă în secțiunea anterioară..
Instruire
-Exercitiul 1
Având în vedere următorii vectori, găsiți vectorul rezultat folosind metoda traversare.
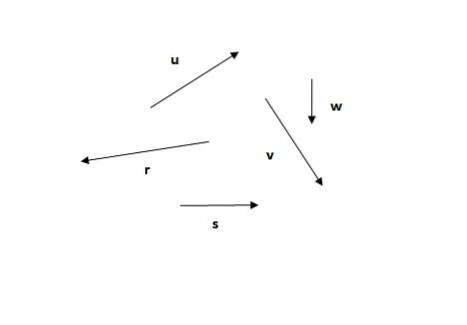
Soluţie
Metoda de traversare este prima dintre metodele văzute. Amintiți-vă că suma vectorilor este comutativă (ordinea addendelor nu modifică suma), deci puteți începe cu oricare dintre vectori, de exemplu sau (figura 5a) sau r (figura 5b):
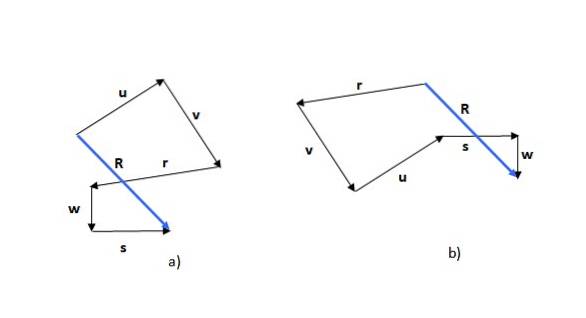
Figura obținută este un poligon și se numește vectorul rezultat (în albastru) R. Dacă începeți cu un alt vector, forma care se formează poate fi diferită, așa cum se poate vedea în exemplu, dar vectorul rezultat este același.
Exercițiul 2
În figura următoare se știe că modulele vectorilor sau Da v respectiv ele sunt u = 3 unități arbitrare și v = 1,8 unități arbitrare. Unghiul care sau forma cu axa x pozitivă este de 45º, în timp ce v formează 60º cu axa y, așa cum se vede în figură. Găsiți vectorul, magnitudinea și direcția rezultate.
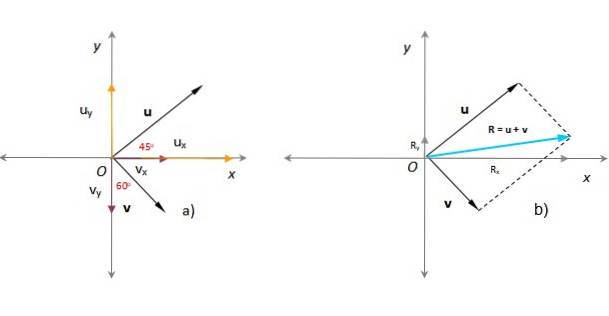
Soluţie
În secțiunea anterioară vectorul rezultat a fost găsit prin aplicarea metodei paralelogramului (în turcoaz din figură).
O modalitate ușoară de a găsi vectorul rezultat analitic este de a exprima vectorii addend în termeni de componente carteziene, ceea ce este ușor atunci când modulul și unghiul sunt cunoscute, cum ar fi vectorii din acest exemplu:
sauX = u. cos 45º = 3 x cos 45º = 2,12; sauDa = u. sin 45º = 3x sin 45º = 2.12
vX = v. sin 60º = 1,8 x sin 60º = 1,56; vDa = -v. cos 60º = -1,8 x cos 60º = - 0,9
Vectori sau Da v sunt vectori aparținând planului, având deci două componente fiecare. Vectorul u se află în primul cadran și componentele sale sunt pozitive, în timp ce vectorul v se află în al patrulea cadran; componenta sa x este pozitivă, dar proiecția sa pe axa verticală cade pe axa y negativă.
Calculul componentelor carteziene ale vectorului rezultat
Vectorul rezultat se găsește prin adăugarea algebrică a respectivelor componente x și y, pentru a obține componentele lor carteziene:
RX = 2,12 + 1,56 = 3,68
RDa = 2,12 + (-0,9) = 1,22
Odată ce componentele carteziene au fost specificate, vectorul este pe deplin cunoscut. Vectorul rezultat poate fi exprimat cu notația între paranteze pătrate (bretele):
R = < 3.68; 1.22> unități arbitrare
Notația cu paranteze pătrate este utilizată pentru a distinge un vector de un punct din plan (sau din spațiu). O altă modalitate de exprimare analitică a vectorului rezultat este folosirea vectorilor unitari eu și j în plan (eu, j Da k in spatiu):
R = 3,68 eu + 1.22 j unități arbitrare
Deoarece ambele componente ale vectorului rezultat sunt pozitive, vectorul R aparține primului cadran, care fusese deja văzut grafic înainte.
Mărimea și direcția vectorului rezultat
Cunoscând componentele carteziene, magnitudinea lui R se calculează prin teorema lui Pitagora, deoarece vectorul rezultat R, împreună cu componentele sale RX și RDa formează un triunghi dreptunghiular:
Magnitudine sau modul: R = (3.68Două + 1.22Două)½ = 3,88
Direcția q luând ca referință axa pozitivă x: q = arctan (RDa / RX) = arctg (1,22 /3,68) = 18,3 º
Referințe
- Adăugarea de vectori și reguli. Adus de la: newt.phys.unsw.edu.au
- Figueroa, D. Seria: Fizică pentru științe și inginerie. Volumul 1. Cinematică 31-68.
- Fizic. Modulul 8: vectori. Recuperat de la: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecanica pentru ingineri. Static. Ediția a 6-a. Compania Editura Continental. 15-53.
- Calculator de adăugare de vectori. Adus de pe: www.1728.org



Nimeni nu a comentat acest articol încă.