viteza unghiulară medie Rotația este definită ca unghiul rotit pe unitatea de timp a vectorului de poziție al unui punct care descrie mișcarea circulară. Paletele unui ventilator de tavan (ca cel prezentat în figura 1), urmează mișcarea circulară și viteza lor unghiulară medie de rotație este calculată luând coeficientul dintre unghiul rotit și timpul în care a fost parcurs acel unghi..
Regulile pe care mișcarea de rotație le urmează sunt oarecum similare cu cele familiare pentru mișcarea de translație. Distanțele parcurse pot fi, de asemenea, măsurate în metri, cu toate acestea magnitudinile unghiulare au o relevanță specială, deoarece facilitează foarte mult descrierea mișcării.
În general, literele grecești sunt utilizate pentru cantitățile unghiulare și literele latine pentru cantitățile liniare corespunzătoare..
Indice articol
Figura 2 reprezintă mișcarea unui punct pe o cale circulară c. Poziția P a punctului corespunde instantului t, iar poziția unghiulară corespunzătoare acelui moment este ϕ.
Din momentul t, se scurge o perioadă de timp Δt. În acea perioadă noua poziție a punctului este P ', iar poziția unghiulară a crescut cu un unghi Δϕ.
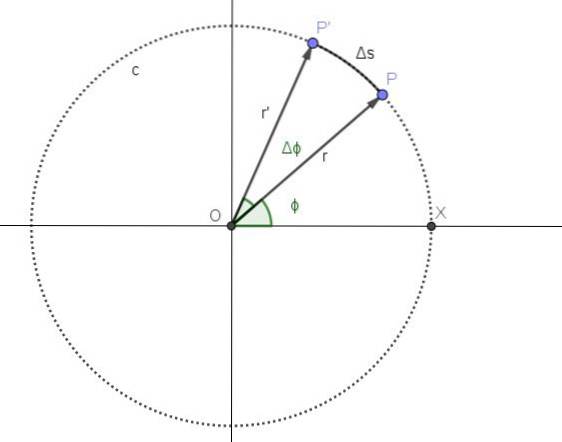
Viteza unghiulară medie ω este unghiul parcurs pe unitate de timp, astfel încât coeficientul Δϕ / Δt va reprezenta viteza unghiulară medie între timpii t și t + Δt:
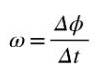
Deoarece unghiul este măsurat în radiani și timpul în secunde, unitatea pentru viteza unghiulară medie este rad / s. Dacă doriți să calculați viteză unghiulară chiar în momentul t, atunci va trebui să calculăm coeficientul Δϕ / Δt când Δt ➡0.
O mișcare de rotație este uniformă dacă, în orice moment observat, unghiul parcurs este același în aceeași perioadă de timp. Dacă rotația este uniformă, atunci viteza unghiulară în orice moment coincide cu viteza unghiulară medie.
Într-o mișcare de rotație uniformă, timpul în care se face o revoluție completă se numește perioadă și este notat cu T.
Mai mult, când se face o rotație completă, unghiul parcurs este de 2π, deci într-o rotație uniformă viteza unghiulară ω este legată de perioada T, prin următoarea formulă:
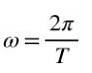
Acesta definește frecvență F a unei rotații uniforme ca coeficientul dintre numărul de rotații și timpul folosit pentru a le parcurge, adică dacă se fac N rotații în perioada de timp thent atunci frecvența va fi:
f = N / Δt
Deoarece se parcurge o rotație (N = 1) în timpul T (perioada), se obține următoarea relație:
f = 1 / T
Adică, într-o rotație uniformă, viteza unghiulară este legată de frecvența prin relația:
ω = 2π ・ f
Viteza liniară v, este coeficientul dintre distanța parcursă și timpul necesar parcurgerii acesteia. În figura 2, distanța parcursă este lungimea arcului Δs.
Arcul Δs este proporțional cu unghiul parcurs Δϕ și raza r, fiind îndeplinită următoarea relație:
Δs = r ・ Δϕ
Atâta timp cât Δϕ este măsurat în radiani.
Dacă împărțim expresia anterioară la intervalul de timp Δt vom obține:
(Δs / Δt) = r ・ (Δϕ / Δt)
Coeficientul primului element este viteza liniară și coeficientul celui de-al doilea element este viteza unghiulară medie:
v = r ・ ω
Vârfurile lamelor ventilatorului de tavan prezentate în figura 1 se mișcă cu o viteză de 5 m / s, iar lamele au o rază de 40 cm.
Cu aceste date, calculați: i) viteza unghiulară medie a roții, ii) numărul de rotații pe care roata le face într-o secundă, iii) perioada în secunde.
i) Viteza liniară este v = 5 m / s.
Raza este r = 0,40 m.
Din relația dintre viteza liniară și viteza unghiulară, rezolvăm pentru aceasta din urmă:
v = r ・ ω => ω = v / r = (5 m / s) / (0,40 m) = 12,57 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 tura / s
iii) T = 1 / f = 1 / (2 ture / s) = 0,5 s pentru fiecare tura.
Un cărucior de jucărie se mișcă pe o pistă circulară cu o rază de 2m. La 0s poziția sa unghiulară este 0 rad, dar după un timp t poziția sa unghiulară este
φ (t) = 2 ・ t .
Cu aceste date
i) Calculați viteza unghiulară medie în următoarele intervale de timp [0s, 0,5s]; [0,5s, 1,0s]; [1,0s, 1,5s] și în cele din urmă în perioada [0,0s, 1,5s].
ii) Pe baza rezultatelor părții i) Ce se poate spune despre mișcare?
iii) Determinați viteza liniară medie în aceeași perioadă de timp din partea i)
iv) Găsiți viteza unghiulară și viteza liniară pentru orice moment.
i) Viteza unghiulară medie este dată de următoarea formulă:
Continuăm să calculăm unghiul parcurs și intervalul de timp scurs în fiecare interval.
Interval 1: Δϕ = ϕ (0,5s) - ϕ (0,0s) = 2 (rad / s) * 0,5s - 2 (rad / s) * 0,0s = 1,0 rad
Δt = 0,5s - 0,0s = 0,5s
ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s
Interval 2: Δϕ = ϕ (1.0s) - ϕ (0.5s) = 2 (rad / s) * 1.0s - 2 (rad / s) * 0.5s = 1.0 rad
Δt = 1,0s - 0,5s = 0,5s
ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s
Interval 3: Δϕ = ϕ (1.5s) - ϕ (1.0s) = 2 (rad / s) * 1.5s - 2 (rad / s) * 1.0s = 1.0 rad
Δt = 1,5s - 1,0s = 0,5s
ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s
Interval 4: Δϕ = ϕ (1.5s) - ϕ (0.0s) = 2 (rad / s) * 1.5s - 2 (rad / s) * 0.0s = 3.0 rad
Δt = 1,5s - 0,0s = 1,5s
ω = Δϕ / Δt = 3.0rad / 1.5s = 2.0 rad / s
ii) Având în vedere rezultatele anterioare, în care viteza unghiulară medie a fost calculată în diferite intervale de timp, obținând întotdeauna același rezultat, pare să indice că este o mișcare circulară uniformă. Cu toate acestea, aceste rezultate nu sunt concludente..
Modul de a asigura concluzia este de a calcula viteza unghiulară medie pentru un interval arbitrar [t, t ']: Δϕ = ϕ (t') - ϕ (t) = 2 * t '- 2 * t = 2 * (t '-t)
Δt = t '- t
ω = Δϕ / Δt = 2 * (t'-t) / (t'-t) = 2,0 rad / s
Aceasta înseamnă că căruciorul de jucărie are o viteză unghiulară medie constantă de 2 rad / s în orice perioadă de timp considerată. Dar puteți merge mai departe dacă calculați viteza unghiulară instantanee:
Acest lucru este interpretat în sensul că mașina de jucărie are în orice moment o viteză unghiulară constantă = 2 rad / s.
Nimeni nu a comentat acest articol încă.