Definiție accelerare centripetă, formule, calcul, exerciții

accelerație centripetă la_c, Numită și radială sau normală, este accelerația pe care o poartă un obiect în mișcare atunci când descrie o cale circulară. Magnitudinea sa este v^Două/ r, Unde r este raza cercului, este direcționată spre centrul acestuia și este responsabilă pentru menținerea mobilului pe drum.

Dimensiunile accelerației centripete sunt lungimea pe unitate de timp la pătrat. În sistemul internațional sunt m / s^Două. Dacă din anumite motive accelerația centripetă dispare, la fel și forța care forțează mobilul să mențină calea circulară.

Așa se întâmplă cu o mașină care încearcă să vireze pe o pistă plană și înghețată, unde fricțiunea dintre sol și roți este insuficientă pentru ca mașina să vireze. Prin urmare, singura posibilitate care rămâne este să vă mișcați în linie dreaptă și de aceea părăsi curba.

Indice articol

• 1 Mișcări circulare
• 2 Forța centripetă
• 3 Formule pentru accelerația centripetă
• 4 Exercițiul a fost rezolvat
  • 4.1 Răspuns
• 5 Referințe

Mișcări circulare

Când un obiect se mișcă în cerc, în orice moment accelerația centripetă este direcționată radial spre centrul circumferinței, direcție perpendiculară pe calea urmată.

Deoarece viteza este întotdeauna tangentă la cale, atunci viteza și accelerația centripetă se dovedesc a fi perpendiculare. Prin urmare, viteza și accelerația nu au întotdeauna aceeași direcție.

În aceste condiții, telefonul mobil are posibilitatea de a descrie circumferința cu viteză constantă sau variabilă. Primul caz este cunoscut sub numele de Mișcare circulară uniformă sau MCU pentru acronim, al doilea caz va fi o mișcare circulară variabilă.

În ambele cazuri, accelerația centripetă este responsabilă pentru menținerea rotirii mobile, asigurându-se că viteza variază numai în direcție și în direcție.

Cu toate acestea, pentru a avea o mișcare circulară variabilă, ar fi necesară o altă componentă a accelerației în aceeași direcție a vitezei, care este însărcinată cu creșterea sau scăderea vitezei. Această componentă a accelerației este cunoscută sub numele de accelerare tangențială.

Mișcarea circulară variabilă și mișcarea curbiliniară în general au ambele componente ale accelerației, deoarece mișcarea curbiliniară poate fi imaginată ca o cale prin nenumărate arce circumferențiale care alcătuiesc calea curbată..

Forța centripetă

Acum, o forță este responsabilă pentru asigurarea accelerației. Pentru un satelit care orbitează pământul, este forța gravitațională. Și întrucât gravitația acționează întotdeauna perpendicular pe traiectorie, nu modifică viteza satelitului..

Într-un astfel de caz gravitația acționează ca un forta centripeta, care nu este o clasă specială sau separată de forță, ci una care, în cazul satelitului, este direcționată radial spre centrul pământului.

În alte tipuri de mișcare circulară, de exemplu o mașină care întoarce o curbă, rolul forței centripete este jucat de frecare statică și pentru o piatră legată de o frânghie care este rotită în cercuri, tensiunea din frânghie este forța care forțează mobil de rotit.

Formule pentru accelerația centripetă

Accelerația centripetă este calculată prin expresia:

ac = v^Două/ r

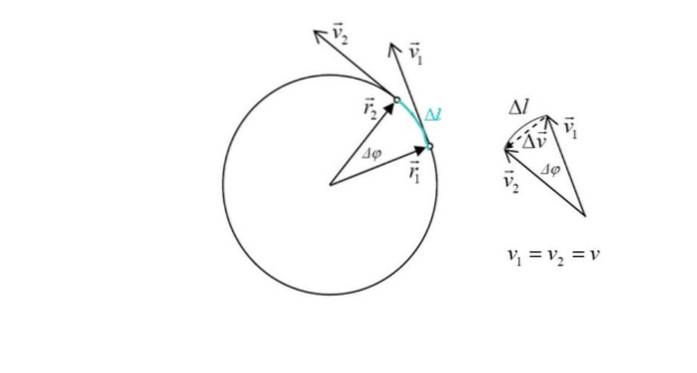
Această expresie va fi derivată mai jos. Prin definiție, accelerația este schimbarea vitezei în timp:

Mobilul durează Δt în traseu, care este mic, deoarece punctele sunt foarte apropiate.

Figura prezintă, de asemenea, doi vectori de poziție r₁ Da r_Două, al cărui modul este același: raza r a circumferinței. Unghiul dintre cele două puncte este Δφ. În verde evidențiază arc traversat de mobil, notat ca Δl.

În figura din dreapta se vede că magnitudinea lui Δv, modificarea vitezei este aproximativ proporțională cu Δl, deoarece unghiul Δφ este mic. Dar schimbarea vitezei este exact legată de accelerație. Din triunghi se poate vedea, prin adăugarea vectorilor care:

v₁ + Δv = v_Două → Δv = v_Două - v₁

Δv este interesant, deoarece este proporțional cu accelerația centripetă. Din figură se poate observa că, din moment ce unghiul Δφ este mic, vectorul Δv este în esență perpendiculară pe ambele v₁ ca v_Două și arată spre centrul circumferinței.

Deși până acum vectorii sunt evidențiați cu caractere aldine, pentru efectele de natură geometrică care urmează, lucrăm cu modulele sau mărimile acestor vectori, renunțând la notația vectorială.

Altceva: trebuie să folosiți definiția unghiului central, care este:

Δφ= Δl / r

Acum sunt comparate ambele cifre, care sunt proporționale de la unghiul Δφ Este comun:

Împărțirea prin Δt:

la_c= v^Două/ r

Exercițiul a fost rezolvat

O particulă se mișcă într-un cerc de rază 2,70 m. La un moment dat, accelerația sa este de 1,05 m / s^Două într-o direcție care face un unghi de 32,0º cu direcția de mișcare. Calculați-vă viteza:

a) În acel moment

b) 2,00 secunde mai târziu, presupunând o accelerație tangențială constantă.

Răspuns

Este o mișcare circulară variată, deoarece afirmația indică faptul că accelerația are un unghi dat cu direcția mișcării care nu este nici 0º (nu poate fi o mișcare circulară) și nici 90º (ar fi o mișcare circulară uniformă).

Prin urmare, cele două componente - radial și tangențial - coexistă. Ele vor fi notate ca a_c deja_t și sunt desenate în figura următoare. Vectorul în verde este vectorul de accelerație netă sau pur și simplu accelerația la.

a) Calculul componentelor de accelerație

la_c = a.cos θ = 1,05 m / s^Două . cos 32,0º = 0,89 m / s^Două (in rosu)

la_t = a.sen θ = 1,05 m / s^Două . sin 32,0º = 0,57 m / s^Două (în portocaliu)

Calculul vitezei telefonului mobil

Din moment ce a_c = v^Două/ r, atunci:

v = v_sau +la_t. t = 1,6 m / s + (0,57 x 2) m / s = 2,74 m / s

Referințe

1. Giancoli, D. Fizică. 2006. Principii cu aplicații. Ediția a șasea. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Științe fizice conceptuale. Ediția a cincea.Pearson.106 - 108.