Concept de cădere liberă, ecuații, exerciții rezolvate

cădere liberă este mișcarea verticală pe care o experimentează un obiect atunci când este aruncat de la o anumită înălțime aproape de suprafața Pământului. Este una dintre cele mai simple și imediate mișcări cunoscute: în linie dreaptă și cu accelerație constantă.

Toate obiectele aruncate sau aruncate vertical în sus sau în jos, se mișcă cu accelerația de 9,8 m / s^Două asigurat de gravitația Pământului, indiferent de masa acestuia.

Astăzi acest fapt poate fi acceptat fără probleme. Cu toate acestea, înțelegerea naturii adevărate a căderii libere a durat ceva timp. Grecii o descriseră și o interpretaseră într-un mod foarte de bază până în secolul al IV-lea î.Hr..

Indice articol

• 1 Ecuații de mișcare de cădere liberă
  • 1.1 Cantități cinematice
  • 1.2 Viteza în funcție de deplasare
• 2 Exemple de cădere liberă
  • 2.1 Accelerarea
  • 2.2 Poziția în funcție de timp: y (t)
  • 2.3 Viteza în funcție de timp: v (t)
  • 2.4 Viteza în funcție de deplasare
  • 2.5 Aruncarea verticală în sus
• 3 exerciții rezolvate
  • 3.1 Exercițiul 1
  • 3.2 Exercițiul 2
• 4 Referințe

Ecuații de mișcare de cădere liberă

Odată convins că accelerația este aceeași pentru toate corpurile eliberate sub acțiunea gravitației, este timpul să stabilim ecuațiile necesare pentru a explica această mișcare..

Este important să subliniem că rezistența la aer nu este luată în considerare în acest prim model de mișcare. Cu toate acestea, rezultatele acestui model sunt foarte precise și apropiate de realitate..

În tot ceea ce urmează, se va presupune modelul de particule, adică dimensiunile obiectului nu sunt luate în considerare, presupunând că toată masa este concentrată într-un singur punct.

Pentru o mișcare rectilinie accelerată uniform în direcția verticală, axa y este luată ca axă de referință. Direcția pozitivă este luată în sus și direcția negativă în jos..

Mărimile cinematice

În acest fel, ecuațiile de poziție, viteză și accelerație în funcție de timp sunt:

Accelerare

a = g = -9,8 m / s^Două (-32 ft / s^Două)

Poziția în funcție de timp: Si t)

y = y_sau + v_sau . t + ½ gt^Două

Unde și_sau este poziția inițială a mobilului și v_sau este viteza inițială. Amintiți-vă că în aruncarea verticală în sus viteza inițială este neapărat diferită de 0.

Care poate fi scris ca:

si si_sau = v_sau . t + ½ gt^Două

Δy = v_sau . t + ½ gt^Două

Cu ΔDa fiind deplasarea efectuată de particula mobilă. În unitățile sistemului internațional, atât poziția, cât și deplasarea sunt date în metri (m).

Viteza în funcție de timp: v (t)

v = v_sau + g. t

Viteza în funcție de deplasare

Este posibil să se obțină o ecuație care leagă deplasarea cu viteza, fără ca timpul să intervină în ea. Pentru aceasta, timpul ultimei ecuații este eliminat:

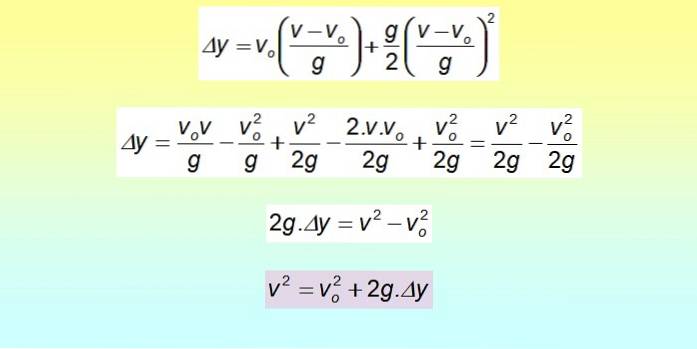
Δy = v_sau . t + ½ gt^Două

Pătratul este dezvoltat cu ajutorul produsului notabil și termenii sunt regrupați.

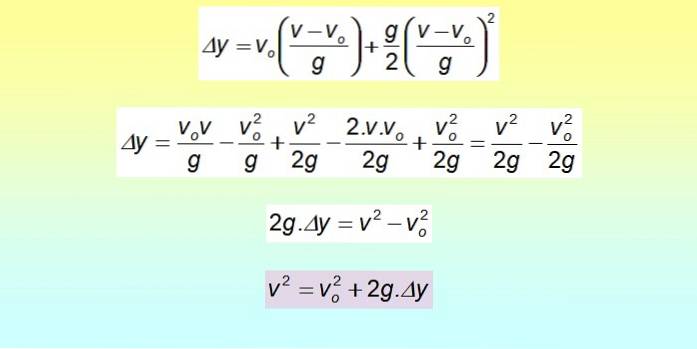
Această ecuație este utilă atunci când nu aveți timp, dar în schimb aveți viteze și deplasări, așa cum veți vedea în secțiunea despre exemple rezolvate..

Exemple de cădere liberă

Cititorul atent va fi observat prezența vitezei inițiale v_sau. Ecuațiile anterioare sunt valabile pentru mișcări verticale sub acțiunea gravitației, atât atunci când obiectul cade de la o anumită înălțime, cât și dacă este aruncat vertical în sus sau în jos.

Când obiectul este scăpat, acesta este pur și simplu făcut v_sau = 0 iar ecuațiile sunt simplificate după cum urmează.

Accelerare

a = g = -9,8 m / s^Două (-32 ft / s^Două)

Poziția în funcție de timp: Si t)

y = y_sau+ ½ gt^Două

Viteza în funcție de timp: v (t)

v = g. t

Viteza în funcție de deplasare

v^Două = 2g. Dy

Dy va fi, de asemenea, negativ, deoarece v^Două trebuie să fie o cantitate pozitivă. Acest lucru se va întâmpla indiferent dacă luați sursă sau zero sistem de coordonate la punctul de lansare sau la sol.

Dacă cititorul preferă, poate lua direcția descendentă ca pozitivă. Gravitația va continua să acționeze dacă se crede că este + 9,8 m / s^Două. Dar trebuie să fiți în concordanță cu convenția semnelor selectate.

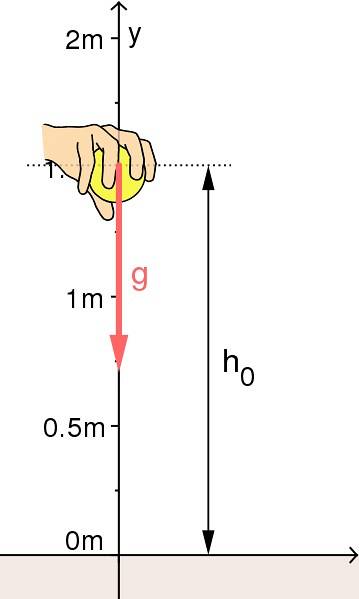
Verticalul aruncă în sus

Aici, desigur, viteza inițială nu poate fi zero. Trebuie să oferiți obiectului un impuls de a se ridica. Conform vitezei inițiale furnizate, obiectul se va ridica la o înălțime mai mare sau mai mică.

Desigur, va exista un moment când obiectul se oprește momentan. Apoi, înălțimea maximă de la punctul de lansare va fi atinsă. De asemenea, accelerația este încă g în jos. Să vedem ce se întâmplă în acest caz.

Calculul înălțimii maxime atinse

Alegerea i = 0:

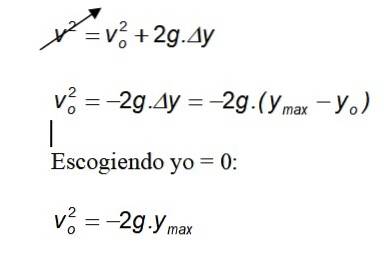
Deoarece gravitația indică întotdeauna spre sol în direcția negativă, semnul negativ este anulat.

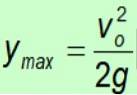
Calculul timpului maxim

O procedură similară este utilizată pentru a găsi timpul necesar obiectului pentru a atinge înălțimea maximă.

v = v_sau + g. t

Da v = 0

v_sau = - g. t_max

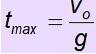
Timpul de zbor este cât durează obiectul în aer. Dacă obiectul revine la punctul de plecare, timpul de creștere este egal cu timpul de coborâre. Prin urmare, timpul de zbor este de 2. t max.

Este de două ori t_max timpul total care durează obiectul în aer? Da, atâta timp cât obiectul pornește dintr-un punct și revine la el.

Dacă lansarea se face de la o anumită înălțime deasupra solului și obiectului i se permite să continue spre el, timpul de zbor nu va mai fi de două ori mai mare decât timpul maxim.

Exerciții rezolvate

În rezoluția exercițiilor următoare, vor fi luate în considerare următoarele:

1-Înălțimea de unde este scăpat obiectul este mică în comparație cu raza Pământului.

2-Rezistența la aer este neglijabilă.

3-Valoarea accelerației gravitației este de 9,8 m / s^Două

4-Când vine vorba de probleme cu un singur mobil, de preferință este ales și_sau = 0 la punctul de plecare. De obicei, acest lucru facilitează calculele..

5-Dacă nu se specifică altfel, direcția verticală în sus este luată ca pozitivă.

6-În mișcările ascendente și descendente combinate, ecuațiile aplicate oferă în mod direct rezultatele corecte, atâta timp cât se menține consistența cu semnele: pozitiv ascendent, negativ descendent și gravitație -9,8 m / s^Două sau -10 m / s^Două dacă se preferă rotunjirea (pentru comoditate la calcul).

Exercitiul 1

O minge este aruncată vertical în sus cu o viteză de 25,0 m / s. Răspunde la următoarele întrebări:

a) Cât de mare este?

b) Cât durează să atingi punctul cel mai înalt?

c) Cât durează mingea să atingă suprafața pământului după ce atinge punctul său cel mai înalt?

d) Care este viteza ta când revii la nivelul de unde ai început?

Soluţie

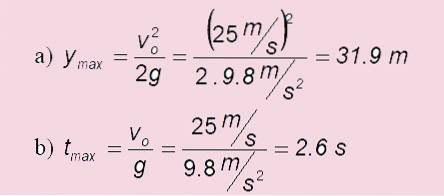
c) În cazul lansării la nivel: t_zbor = 2. t_max = 2 x6 s = 5,1 s

d) Când revine la punctul de plecare, viteza are aceeași magnitudine ca viteza inițială, dar în direcția opusă, deci trebuie să fie - 25 m / s. Se verifică cu ușurință prin înlocuirea valorilor în ecuație cu viteza:

Exercițiul 2

O mică geantă poștală este eliberată dintr-un elicopter care coboară cu o viteză constantă de 1,50 m / s. După 2.00 s calculați:

a) Care este viteza valizei?

b) Cât de departe este valiza sub elicopter?

c) Care sunt răspunsurile dvs. pentru părțile a) și b) dacă elicopterul crește cu o viteză constantă de 1,50 m / s?

Soluţie

Paragraful a

Prin urmare, la ieșirea din elicopter, geanta poartă viteza inițială a elicopterului v_sau = -1,50 m / s. Cu timpul indicat, viteza a crescut datorită accelerației gravitației:

v = v_sau + g. t = -1,50 - (9,8 x 2) m / s = - 21,1 m / s

Secțiunea b

Să vedem cât a scăzut valiza de la punctul de plecare în acel moment:

Valiză: Dy = v_sau . t + ½ gt^Două = -1,50 x 2 + ½ (-9,8) x 2^Două m = -22,6 m

A fost selectat Da_sau = 0 la punctul de plecare, așa cum este indicat la începutul secțiunii. Semnul negativ indică faptul că valiza a coborât cu 22,6 m sub punctul de plecare..

Între timp elicopterul A căzut cu o viteză de -1,50 m / s, presupunem cu viteză constantă, prin urmare, în timpul indicat de 2 secunde, elicopterul a parcurs:

Elicopter: Δy = v_sau.t = -1,50 x 2 m = -3 m.

Prin urmare, după 2 secunde, valiza și elicopterul sunt separate de o distanță de:

d =| -22,6 - (-3) | m = 19. 6 m.

Distanța este întotdeauna pozitivă. Pentru a evidenția acest fapt, se folosește valoarea absolută.

Secțiunea c

Când elicopterul se ridică, acesta are o viteză de + 1,5 m / s. Cu această viteză, valiza iese, astfel încât după 2 secunde are deja:

v = v_sau + g. t = +1,50 - (9,8 x 2) m / s = - 18,1 m / s

Viteza se dovedește a fi negativă, deoarece după 2 secunde geanta se deplasează în jos. A crescut datorită gravitației, dar nu la fel de mult ca în secțiunea a.

Acum, să aflăm cât a coborât valiza de la punctul de plecare în primele 2 secunde de călătorie:

Geanta: Δy = v_sau . t + ½ gt^Două = +1,50 x 2 + ½ (-9,8) x 2^Două m = -16,6 m

Între timp, elicopterul a crescut față de punctul de plecare și a făcut-o cu viteză constantă:

Elicopter: Δy = v_sau.t = +1,50 x 2 m = +3 m.

După 2 secunde, valiza și elicopterul sunt separate de o distanță de:

d =| -16,6 - (+3) | m = 19,6 m

Distanța care le separă este aceeași în ambele cazuri. Valiza parcurge o distanță mai mică pe verticală în al doilea caz, deoarece viteza sa inițială a fost îndreptată în sus..

Referințe

1. Kirkpatrick, L. 2007. Fizica: O privire asupra lumii. 6^ta Ediție scurtată. Cengage Learning. 23 - 27.
2. Rex, A. 2011. Fundamentele fizicii. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14^a. Ed. Volumul 1. 50 - 53.
4. Serway, R., Vulle, C. 2011. Fundamentele fizicii. 9^{n / A} Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fizică 10. Pearson Education. 133 - 149.