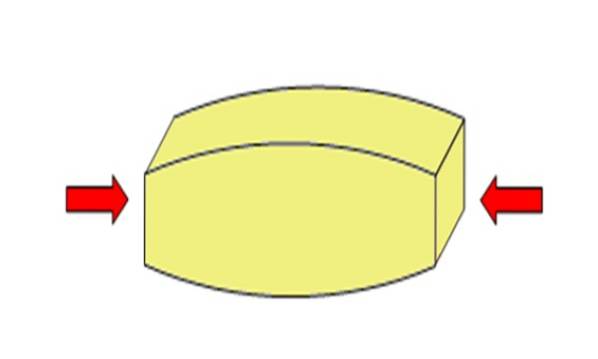
compresie sau stres compresiv este forța pe unitate de suprafață al cărei rezultat este împingerea, stoarcerea sau comprimarea unui obiect, având tendința de a-l scurta. Matematic este:
E = F / A
Aici ȘI denotă efort, F amploarea forței și LA zona pe care acționează, unitatea din Sistemul Internațional SI fiind newtonul / mDouă sau pascal (Pa). Stresul compresiv este un efort normal, deoarece forța care o produce este perpendiculară pe aria asupra căreia se exercită.
Un astfel de efort poate comprima obiectul sau, dimpotrivă, îl poate întinde și întinde, după cum este aplicat. În cazul stresului de compresiune, forțele sunt aplicate în direcția opusă pentru a exercita efectul stoarcerii și scurtării obiectului.
Odată ce forțele încetează, multe materiale revin la dimensiunile lor originale. Această proprietate este cunoscută sub numele de elasticitate. Dar, în timp ce se întâmplă acest lucru, deformarea unității elastice suferită de un material supus unei solicitări este:
Tulpina = (Dimensiune finală - Dimensiune inițială) / Dimensiune inițială
Tulpina poate fi liniară, de suprafață sau volumetrică, deși tulpina este fără unitate. Cu toate acestea, informațiile pe care le furnizează sunt foarte importante, deoarece nu este același lucru să deformezi o bară lungă de 10 m cu 1 cm, să deformezi încă o bară lungă de 1 m cu 1 cm.
Într-un material elastic, deformarea și tensiunea sunt proporționale, îndeplinind legea lui Hooke:
Efort ∝ Deformarea unității
Indice articol
Stresul de compresiune face ca particulele materialului să se apropie din ce în ce mai mult, reducând dimensiunea acestora. În funcție de direcția în care este aplicat efortul, va exista o scurtare sau reducere a unora dintre dimensiunile sale.
Să începem prin a presupune o bară subțire de lungime originală L, la care stresul normal de mărime ȘI. Dacă tensiunea este compresivă, bara experimentează o reducere a lungimii sale, notată cu δ. Dacă este tensiune, bara se va prelungi.
Bineînțeles, materialul din care este fabricat elementul este decisiv în capacitatea sa de a rezista la stres..
Aceste caracteristici elastice ale materialului sunt incluse în constanta de proporționalitate menționată anterior. Se numeste modul de elasticitate sau Modulul lui Young și este notat ca Y. Fiecare material are un modul de elasticitate, care este determinat experimental prin teste de laborator.
Având în vedere acest lucru, efortul ȘI Este exprimat în formă matematică astfel:
Efort ∝ Deformarea unității
În cele din urmă, pentru a stabili această condiție ca o ecuație, este necesară o constantă de proporționalitate pentru a înlocui simbolul proporționalității ∝ și a-l înlocui cu egalitatea, astfel:
Stres = Constanta de proportionalitate x Unitatea de tensiune
E = Y. (δ / L)
Coeficientul (δ / L) este tulpina, notată ca ε și cu δ = Lungimea finală - Lungimea inițială. În acest fel, efortul ȘI se pare ca:
E = Y. ε
Deoarece tulpina este adimensională, unitățile de Da sunt la fel ca cele ale ȘI: N / mDouă o Pa în sistemul SI, lire / inDouă sau psi în sistemul britanic, precum și alte combinații de forță și zonă, cum ar fi kg / cmDouă.
Valorile Y sunt determinate experimental în laborator, în condiții controlate. Apoi, modulul de elasticitate pentru materialele utilizate pe scară largă în construcții și, de asemenea, cel al oaselor:
tabelul 1
| Material | Modul de elasticitate Y (Pa) x 109 |
|---|---|
| Oţel | 200 |
| Fier | 100 |
| Alamă | 100 |
| Bronz | 90 |
| Aluminiu | 70 |
| Marmură | cincizeci |
| Granit | Patru cinci |
| Beton | douăzeci |
| Os | cincisprezece |
| Pin de pin | 10 |
Forțele de compresie acționează asupra diverselor structuri; Acestea sunt supuse acțiunii unor forțe precum greutatea fiecăruia dintre elementele care le compun, precum și forțelor de la agenți externi: vânt, zăpadă, alte structuri și multe altele..
Este obișnuit ca majoritatea structurilor să fie proiectate pentru a rezista la solicitări de toate tipurile fără a se deforma. Prin urmare, tensiunea de compresie trebuie luată în considerare pentru a preveni pierderea formei piesei sau obiectului..
De asemenea, oasele scheletului sunt structuri supuse la diverse tensiuni. Deși oasele sunt rezistente la ele, atunci când din greșeală se depășește limita elastică, se produc fisuri și fracturi.
Coloanele și pilonii de construcție trebuie să fie făcute pentru a rezista la compresiune, altfel tind să se plece. Acest lucru este cunoscut sub numele de îndoire laterală sau flambând.
Coloanele (vezi figura 1) sunt elemente a căror lungime este considerabil mai mare în comparație cu aria secțiunii lor transversale..
Un element cilindric este o coloană atunci când lungimea sa este egală sau mai mare de zece ori diametrul secțiunii transversale. Dar dacă secțiunea transversală nu este constantă, diametrul său mai mic va fi luat pentru a clasifica elementul ca o coloană.
Când oamenii se așează pe mobilier, cum ar fi scaune și bănci, sau adaugă obiecte deasupra, picioarele sunt supuse unor solicitări de compresiune care tind să scadă înălțimea lor..
Mobilierul este de obicei făcut să reziste destul de bine la greutate și revine la starea sa naturală odată ce a fost îndepărtat. Dar dacă greutatea mare este plasată pe scaune sau bănci fragile, picioarele lasă loc la compresiune și rupere..
Există o tijă care măsoară inițial 12 m lungime, la care este supusă unei solicitări de compresiune, astfel încât unitatea sa de deformare este de -0.0004. Care este noua lungime a tijei?
Pornind de la ecuația dată mai sus:
ε = (δ / L) = - 0,0004
da LF este lungimea finală și Lsau lungimea inițială, din moment ce δ = LF - Lsau aveți:
(LF - Lsau) / Lsau = -0.0004
Prin urmare: LF - Lsau = -0.0004 x 12 m = -0.0048 m. Și, în sfârșit:
LF = (12 - 0,0048) m = 11,9952 m.
O bară de oțel solidă, de formă cilindrică, are 6 m lungime și 8 cm diametru. Dacă bara este comprimată cu o sarcină de 90.000 kg, găsiți:
a) Mărimea stresului de compresiune în megapascali (MPa)
b) Cu cât a scăzut lungimea barei?
Mai întâi găsim zona A a secțiunii transversale a barei, care depinde de diametrul său D, rezultând:
A = π. DDouă / 4 = π. (0,08 m)Două / 4 = 5,03 x 10-3 mDouă
Forța este imediat găsită, prin F = m.g = 90.000 kg x 9,8 m / sDouă= 882.000 N.
În cele din urmă, efortul mediu este calculat astfel:
E = F / A = 882.000 N / 5,03 x 10-3 mDouă = 1,75 x 108 Pa = 175 MPa
Acum se folosește ecuația pentru stres, știind că materialul are un răspuns elastic:
E = Y. (δ / L)
Modulul de oțel al lui Young se găsește în Tabelul 1:
δ = E.L / Y = 6 m x 1,75 x 108 Pa / 200 x 10 9 Pa = 5,25 x 10 -3 m = 5,25 mm.
Nimeni nu a comentat acest articol încă.