
Conceptul de condiții de echilibru, aplicații și exemple
condiții de echilibru Sunt necesare pentru ca un corp să rămână în repaus sau în mișcare rectilinie uniformă. În primul caz se spune că obiectul este în echilibru static, în timp ce în al doilea este în echilibru dinamic.
Presupunând că obiectul în mișcare este o particulă, caz în care dimensiunile nu sunt luate în considerare, este suficient ca suma forțelor care acționează asupra acestuia să fie anulată..

Dar o mare majoritate a obiectelor în mișcare au dimensiuni apreciabile, prin urmare această condiție nu este suficientă pentru a garanta echilibrul, care în orice caz este absența accelerației, nu a mișcării..
Indice articol
- 1 Prima și a doua condiție de echilibru
- 2 Aplicații
- 2.1 Echilibrul izostatic
- 2.2 Cum funcționează fuziunea în nucleu
- 2.3 Construcție
- 3 Tipuri de echilibru static
- 3.1 Echilibru stabil
- 3.2 Echilibru indiferent sau neutru
- 3.3 Echilibru instabil
- 4 Exemplu: statica particulelor
- 5 Exercițiul a fost rezolvat
- 5.1 Soluție
- 6 Subiecte de interes
- 7 Referințe
Prima și a doua condiție de echilibru
Să vedem: dacă suma forțelor este zero, este adevărat că obiectul nu se va mișca sau se va deplasa cu o viteză accelerată, dar ar putea începe totuși să se rotească.
Prin urmare, pentru a evita rotațiile, trebuie adăugată o a doua condiție: să fie anulată și suma cuplurilor sau momentelor de torsiune cauzate de forțele externe care acționează asupra ei, în jurul oricărui punct..
Pe scurt, denotând ca F vectorul de forță netă y τ sau M la vectorul cuplului net, vom avea:
Prima condiție de echilibru
∑ F = 0
Ceea ce înseamnă că: ∑ FX = 0, ∑ FDa = 0 și ∑ Fz = 0
A doua condiție de echilibru
∑ τ = 0 sau ∑ M = 0
Cu cuplurile sau momentele calculate despre orice punct.
În cele ce urmează vom presupune că obiectul în mișcare este un corp rigid, unul care nu suferă nicio deformare..
Aplicații
În ciuda faptului că mișcarea pare a fi numitorul comun în univers, echilibrul este prezent și în multe aspecte ale naturii și în obiectele care ne înconjoară..
Echilibrul izostatic
La scară planetară, Pământul se află echilibru izostatic, un fel de echilibru gravitațional al scoarței terestre, a cărui densitate nu este uniformă.
Diferențele de densitate ale diferitelor blocuri sau zone ale scoarței terestre sunt compensate de diferențele de înălțime care caracterizează orografia planetei. Funcționează în același mod în care diferite materiale sunt mai mult sau mai puțin scufundate în apă în funcție de densitatea lor și ajung la echilibru.
Dar, din moment ce blocurile scoarței nu plutesc corect în apă, ci în manta, care este mult mai vâscoasă, echilibrul nu se numește hidrostatic, ci izostatic..
Cum funcționează fuziunea în nucleu
La stele precum Soarele nostru, echilibrul dintre forța de greutate care le comprimă și presiunea hidrostatică care le extinde, menține reactorul de fuziune din miezul stelei în funcțiune, care îl menține în viață. Depindem de acest echilibru pentru ca Pământul să primească lumina și căldura necesare.
Clădire
La scară locală, dorim ca clădirile și construcțiile să rămână stabile, adică să respecte condițiile de echilibru, în special echilibrul static..
De aceea a apărut statica, care este ramura mecanicii dedicate studierii echilibrului corpurilor și a tot ceea ce este necesar pentru a le menține astfel..
Tipuri de echilibru static
În practică, constatăm că echilibrul static poate fi de trei feluri:
Echilibru stabil
Apare atunci când obiectul se deplasează din poziția sa și revine imediat la el când încetează forța care l-a împins. Cu cât un obiect este mai aproape de sol, cu atât este mai probabil să se afle într-un echilibru stabil.
Mingea din dreapta din figura 2 este un bun exemplu, dacă o scoatem din poziția sa de echilibru din partea de jos a bolului, gravitația se va ocupa de revenirea sa rapidă.
Echilibru indiferent sau neutru
Apare atunci când obiectul, în ciuda faptului că a fost mutat, este încă în echilibru. Obiectele rotunde, cum ar fi mingea, atunci când sunt așezate pe suprafețe plane sunt în echilibru indiferent.
Echilibru instabil
Apare atunci când obiectul se deplasează din poziția sa de echilibru, nu se întoarce la el. Dacă mutăm mingea departe de vârful dealului din stânga, este sigur că nu se va întoarce sub propria sa putere..

Exemplu: statica particulelor
Să presupunem că un bloc de masă m pe un plan înclinat, din care se presupune că toată masa este concentrată în centrul său geometric.
Componenta orizontală a greutății WX tinde să facă blocul să alunece în jos, de aceea este nevoie de o altă forță opusă. Dacă vrem ca blocul să rămână în repaus, această forță este fricțiunea statică. Dar dacă permitem blocului să alunece în jos cu viteză constantă, atunci forța necesară este fricțiunea dinamică..
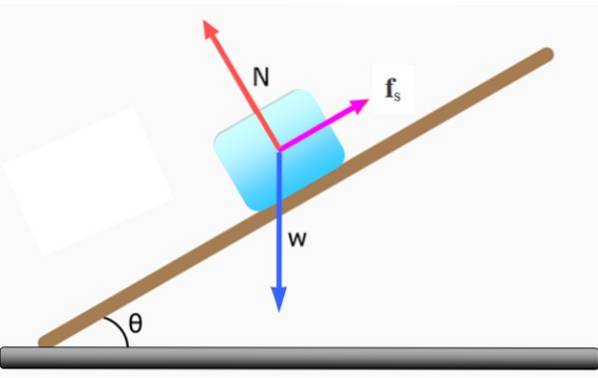
În absența fricțiunii, blocul va aluneca rapid în jos și în acest caz nu va exista echilibru.
Pentru ca blocul să fie în repaus, forțele care acționează asupra acestuia: greutatea W, normalul N și fricțiunea statică Fs, acestea trebuie compensate. Atunci:
∑ FDa = 0 → N - WDa = 0
∑ FX = 0 → WX - Fs = 0
Fricțiunea statică echilibrează componenta orizontală a greutății: WX = fs prin urmare:
Fs = m. g .sen θ
Exercițiul a fost rezolvat
Un semafor de 21,5 kg atârnă de o bară omogenă de aluminiu AB cu o masă de 12 kg și o lungime de 7,5 m, susținută de un cablu orizontal CD, așa cum se arată în figură. Găsi:
a) Tensiunea cablului de curent continuu
b) Componentele orizontale și verticale ale forței exercitate de pivotul A pe stâlp.
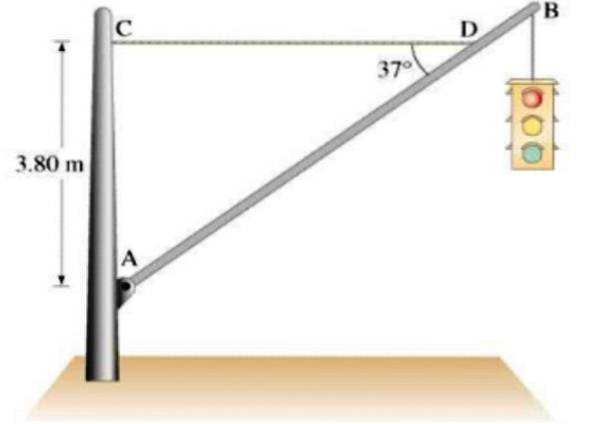
Soluţie
Se construiește diagrama forțelor aplicate barei, cu greutatea W, tensiunile din acorduri și componentele orizontale și verticale ale reacției pivot, numite RX și RDa. Atunci se aplică condiții de echilibru.
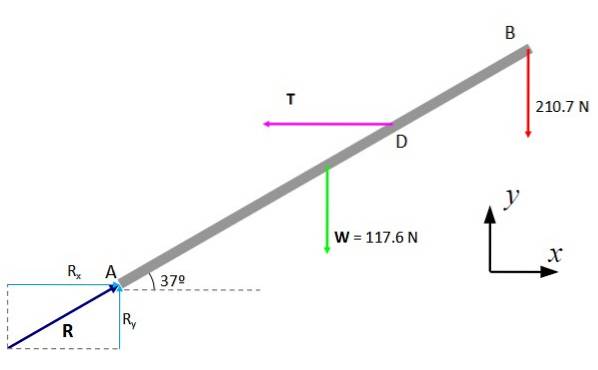
Prima condiție
Fiind o problemă în plan, prima condiție de echilibru oferă două ecuații:
ΣFX = 0
ΣFDa = 0
Din prima:
RX - T = 0
RX = T
Și al doilea:
RDa - 117,6 N - 210,7 N = 0
RDa = 328,3 N
Componenta orizontală a reacției este egală în mărime cu tensiunea T.
A doua condiție
Punctul A din figura 5 este ales ca centru de rotație, în acest fel brațul de reacție R este nul, amintiți-vă că magnitudinea momentului este dată de:
M = F┴ d
Unde F┴ este componenta perpendiculară a forței și d este distanța dintre axa de rotație și punctul de aplicare a forței. Vom obține o ecuație:
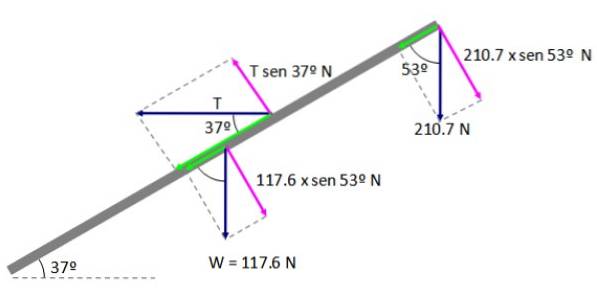
ΣMLA = 0
(210,7 × sin 53º) AB + (117,6 × sin 53º) (AB / 2) - (T × sin 37º) AD = 0
Distanța AD este:
AD = (3,8 m / sin 37º) = 6,3 m
(210,7 × sin 53º N) (7,5 m) + (117,6 × sin 53º N) (3,75 m) - (T × sin 37º N) (6,3 m) = 0
Efectuarea operațiunilor indicate:
1262,04 + 352,20 - 3,8T = 0
Rezolvând pentru T, obținem:
T = 424,8 N
Din prima condiție, RX = T, deci:
RX = 424,8 N
Teme de interes
Prima condiție de echilibru.
A doua condiție de echilibru.
Referințe
- Bedford, 2000. A. Mecanica inginerească: statică. Addison Wesley.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 4. Sisteme de particule. Editat de Douglas Figueroa (USB).
- Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1.
- Wikipedia. Isostasia. Recuperat de pe: es.wikipedia.org.


Nimeni nu a comentat acest articol încă.