
Exemple de coordonate sferice și exerciții rezolvate

coordonate sferice sunt un sistem de localizare punctuală în spațiu tridimensional format dintr-o coordonată radială și două coordonate unghiulare numite coordonate polare și coordonate azimutale.
Figura 1, pe care o vedem mai jos, prezintă coordonatele sferice (r, θ, φ) ale unui punct M. Aceste coordonate sunt referite la un sistem ortogonal de axe cartesiene X, Y, Z de origine O.
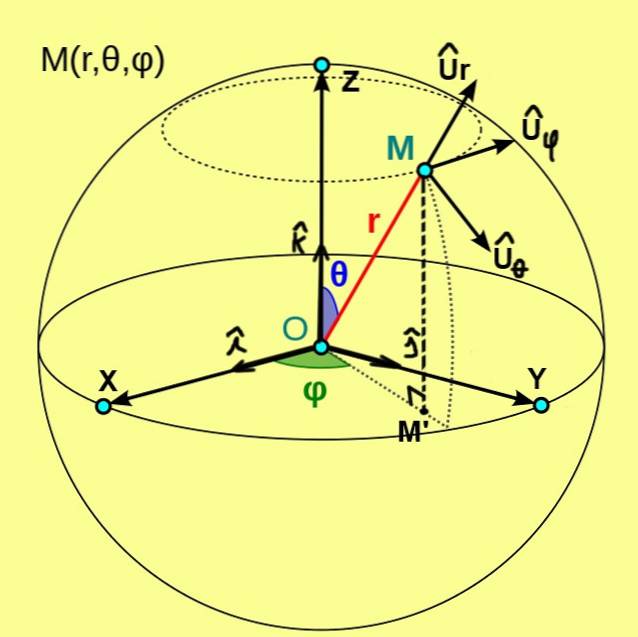
În acest caz, coordonata r a punctului M este distanța de la acel punct la originea O. Coordonata polară θ reprezintă unghiul dintre semi-axa pozitivă Z și vectorul de rază OM. În timp ce coordonata azimutală φ este unghiul dintre semi-axa pozitivă X și vectorul de rază OM ', unde M' este proiecția ortogonală a lui M pe planul XY.
Coordonata radială r ia doar valori pozitive, dar dacă un punct este situat la origine, atunci r = 0. Coordonata polară θ ia ca valoare minimă 0º pentru punctele situate pe semi-axa Z pozitivă și o valoare maximă 180º pentru puncte este situată pe semi-axa Z negativă. În cele din urmă, coordonata azimutală φ ia ca valoare minimă 0º și o înălțime maximă de 360 °.
0 ≤ r < ∞
0 ≤ θ ≤ 180º
0 ≤ φ < 360º
Indice articol
- 1 Schimbarea coordonatelor
- 1.1 Baza vectorială în coordonate sferice
- 1.2 Elemente de linie și volum în coordonate sferice
- 2 Relația cu coordonatele geografice
- 2.1 Formule de schimbare de la geografice la sferice
- 3 Exemple
- 3.1 Exemplul 1
- 3.2 Exemplul 2
- 4 Exerciții
- 4.1 Exercițiul 1
- 4.2 Exercițiul 2
- 5 Referințe
Schimbarea coordonatelor
Formulele care permit obținerea coordonatelor carteziene (x, y, z) ale unui punct M vor fi date mai jos, presupunând că coordonatele sferice ale aceluiași punct (r, θ, φ) sunt cunoscute:
x = r Sen (θ) Cos (φ)
y = r Sen (θ) Sen (φ)
z = r Cos (θ)
În același mod, este util să găsiți relațiile pentru a merge de la coordonatele carteziene (x, y, z) ale unui punct dat la coordonatele sferice ale punctului menționat:
r = √ (x ^ 2 + y ^ 2 + z ^ 2)
θ = Arctan (√ (x ^ 2 + y ^ 2) / z)
φ = Arctan (y / x)
Baza vectorială în coordonate sferice
Din coordonatele sferice se definește o bază ortonormală a vectorilor de bază, care sunt notați cu Ur, Uθ, Uφ. Figura 1 prezintă acești trei vectori unitari, care au următoarele caracteristici:
- Ur este vectorul unitar tangent la linia radială θ = ctte și φ = ctte;
- Uθ este vectorul unitar tangent la arc φ = ctte și r = ctte;
- Uφ este vectorul unitar tangent la arc r = ctte și θ = ctte.
Elemente de linie și volum în coordonate sferice
Vectorul de poziție al unui punct din spațiu în coordonate sferice este scris astfel:
r = r Ur
Dar o variație sau deplasare infinitesimală a unui punct în spațiul tridimensional, în aceste coordonate, este exprimată prin următoarea relație vectorială:
dr = dr Ur + r dθ Uθ + r Sen (θ) dφ Uφ
În sfârșit, un volum infinitesimal dV în coordonate sferice este scris astfel:
dV = r ^ 2 Sen (θ) dr dθ dφ
Aceste relații sunt foarte utile pentru calcularea integralelor de linie și volum în situații fizice care au simetrie sferică..
Relația cu coordonatele geografice
Coordonatele geografice sunt înțelese ca fiind cele care servesc la localizarea locurilor de pe suprafața pământului. Acest sistem folosește coordonatele de latitudine și longitudine pentru a localiza poziția pe suprafața Pământului..
În sistemul de coordonate geografice, se presupune că suprafața pământului este sferică cu raza Rt, chiar dacă se știe că este aplatizată la poli și se consideră un set de linii imaginare numite paralele și meridiane.
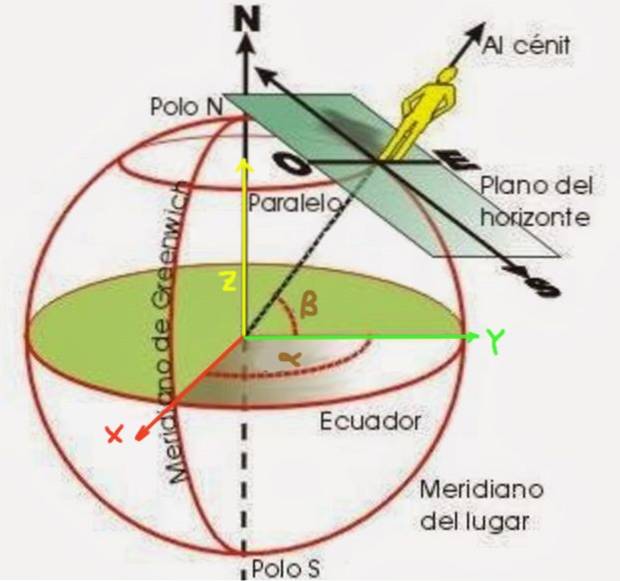
Latitudinea β este un unghi format dintr-o rază care începe de la centrul Pământului până la punctul pe care doriți să îl poziționați. Se măsoară din planul ecuatorial, așa cum se arată în figura 2. Pe de altă parte, longitudinea α este unghiul pe care îl formează meridianul punctului care se află în raport cu meridianul zero (cunoscut sub numele de meridianul Greenwich).
Latitudinea poate fi latitudine nordică sau sudică, în funcție de dacă locul pe care îl localizați este în emisfera nordică sau în emisfera sudică. În mod similar, longitudinea poate fi la vest sau la est, în funcție de locația situată la vest sau la est de meridianul zero..
Formule de schimbare de la geografice la sferice
Pentru a obține aceste formule, primul lucru este să stabiliți un sistem de coordonate. Planul XY este ales să coincidă cu planul ecuatorial, semi-axa X pozitivă fiind cea care merge de la centrul Pământului și trece prin meridianul zero. La rândul său, axa Y trece prin meridianul 90º E. Suprafața pământului are o rază Rt.
Cu acest sistem de coordonate, transformările de la geografice la sferice arată astfel:
αEβN → (Rt, θ = 90º-β, φ = α)
αOβN → (Rt, θ = 90º-β, φ = 360º-α)
αEβS → (Rt, θ = 90º + β, φ = α)
αOβS → (Rt, θ = 90º + β, φ = 360º-α)
Exemple
Exemplul 1
Coordonatele geografice din Palma de Mallorca (Spania) sunt:
Longitudine estică 38.847º și latitudine nordică 39.570º. Pentru a determina coordonatele sferice corespunzătoare Palma de Mallorca, se aplică prima dintre formulele formulelor din secțiunea anterioară:
38.847ºE39.570ºN → (r = 6371 km, θ = 90º-39.570º, φ = 38.847º)
Deci coordonatele sferice sunt:
Palma de Mallorca: (r = 6371 km, θ = 50,43º, φ = 38,85º)
În răspunsul anterior am luat r egal cu raza medie a Pământului.
Exemplul 2
Știind că Insulele Falkland (Malvinas) au coordonate geografice de 59ºO 51,75ºS, determinați coordonatele polare corespunzătoare. Amintiți-vă că axa X merge de la centrul Pământului la meridianul 0º și pe planul ecuatorial; axa Y, de asemenea, în planul ecuatorial și care trece prin meridianul 90º Vest; în cele din urmă, axa Z pe axa de rotație a Pământului în direcția Sud-Nord.
Pentru a găsi apoi coordonatele sferice corespunzătoare folosim formulele prezentate în secțiunea anterioară:
59ºO 51,75ºS → (r = 6371 km, θ = 90º + 51,75º, φ = 360º-59º) adică
Falklands: (r = 6371 km, θ = 141.75º, φ = 301º)
Instruire
Exercitiul 1
Găsiți coordonatele carteziene din Palma de Mallorca în sistemul de referință cartezian XYZ prezentat în figura 2.
Soluţie: Anterior, în exemplul 1, coordonatele sferice erau obținute pornind de la coordonatele geografice din Palma de Mallorca. Deci, formulele prezentate mai sus pot fi folosite pentru a merge de la sferic la cartezian:
x = 6371 km Sen (50,43º) Cos (38,85º)
y = 6371 km Sen (50,43º) Sen (38,85º)
z = 6371 km Cos (50,43º)
Efectuând calculele corespunzătoare avem:
Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)
Exercițiul 2
Găsiți coordonatele carteziene ale insulelor Falkland în sistemul de referință cartezian XYZ prezentat în figura 2.
Soluţie: Anterior, în exemplul 2, coordonatele sferice erau obținute pornind de la coordonatele geografice ale insulelor Falkland. Deci, formulele prezentate mai sus pot fi folosite pentru a merge de la sferic la cartezian:
x = 6371 km Sen (141.75º) Cos (301º)
y = 6371 km Sen (141.75º) Sen (301º)
z = 6371 km Cos (141.75º)
Efectuând calculele corespunzătoare, obținem:
Insulele Falkland: (x = 2031 km, y = -3381 km, z = -5003)
Referințe
- Arfken G și Weber H. (2012). Metode matematice pentru fizicieni. Un ghid cuprinzător. Ediția a VII-a. Academic Press. ISBN 978-0-12-384654-9
- Calcul cc. S-au rezolvat probleme de coordonate cilindrice și sferice. Recuperat de la: calculo.cc
- Atelier de astronomie. Latitudine și longitudine. Recuperat de pe: tarifamates.blogspot.com/
- Weisstein, Eric W. „Coordonatele sferice”. De la MathWorld-A Wolfram Web. Recuperat de pe: mathworld.wolfram.com
- wikipedia. Sistem de coordonate sferice. Recuperat de pe: en.wikipedia.com
- wikipedia. Câmpuri vectoriale în coordonate cilindrice și sferice. Recuperat de pe: en.wikipedia.com



Nimeni nu a comentat acest articol încă.