Care este perioada funcției y = 3sen (4x)?

perioada funcției y = 3sen (4x) este 2π / 4 = π / 2. Pentru a înțelege clar motivul acestei afirmații, trebuie cunoscută definiția perioadei unei funcții și a perioadei funcției sin (x); un pic despre graficarea funcțiilor va fi, de asemenea, util.

Funcțiile trigonometrice, cum ar fi sinusul și cosinusul (sin (x) și cos (x)), sunt foarte utile atât în ​​matematică, cât și în inginerie.

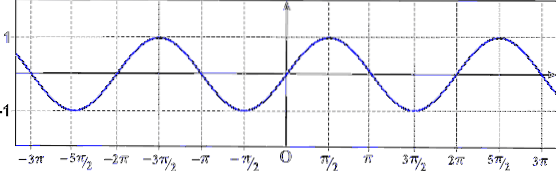
Cuvântul perioadă se referă la repetarea unui eveniment, deci a spune că o funcție este periodică echivalează cu a spune „graficul său este repetarea unei bucăți de curbă”. După cum se poate vedea în imaginea anterioară, funcția sin (x) este periodică.

Funcții periodice

Se spune că o funcție f (x) este periodică dacă există o valoare reală p ≠ 0 astfel încât f (x + p) = f (x) pentru toate x din domeniul funcției. În acest caz, perioada funcției este p.

Perioada funcției se numește, în general, cel mai mic număr real pozitiv p care satisface definiția.

Așa cum se poate vedea în graficul anterior, funcția sin (x) este periodică și perioada sa este 2π (funcția cosinusului este, de asemenea, periodică, cu o perioadă egală cu 2π).

Modificări în graficul unei funcții

Fie f (x) o funcție al cărei grafic este cunoscut și fă c o constantă pozitivă. Ce se întâmplă cu graficul lui f (x) dacă f (x) este înmulțit cu c? Cu alte cuvinte, care este graficul lui c * f (x) și f (cx)?

Graficul lui c * f (x)

Când înmulțiți o funcție, extern, cu o constantă pozitivă, graficul lui f (x) suferă o modificare a valorilor de ieșire; adică schimbarea este verticală și există două cazuri:

- Dacă c> 1, atunci graficul suferă o întindere verticală cu un factor de c.

- Da 0

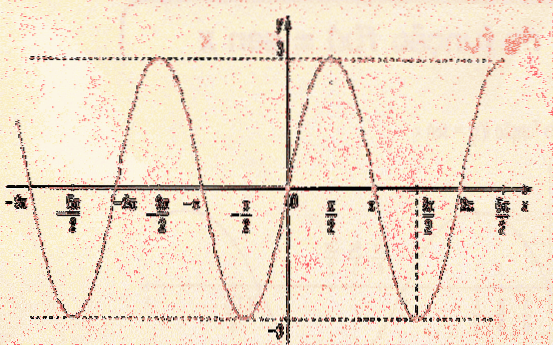
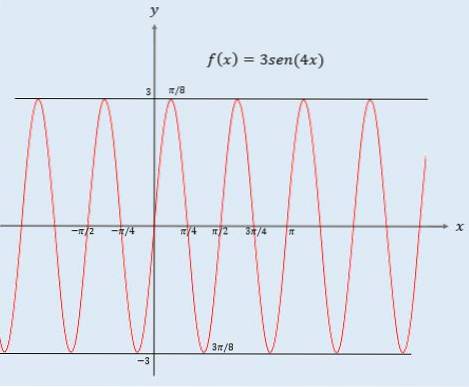
Graficul lui f (cx)

Când argumentul unei funcții este înmulțit cu o constantă, graficul lui f (x) suferă o modificare a valorilor de intrare; adică schimbarea este orizontală și, ca și până acum, pot exista două cazuri:

- Dacă c> 1, atunci graficul suferă o compresie orizontală cu un factor de 1 / c.

- Da 0

Perioada funcției y = 3sen (4x)

Trebuie remarcat faptul că în funcția f (x) = 3sen (4x) există două constante care modifică graficul funcției sinusoidale: una înmulțindu-se extern și cealaltă intern..

3 care se află în afara funcției sinusoidale, ceea ce face este să alungește funcția pe verticală cu un factor 3. Acest lucru implică faptul că graficul funcției 3 sin (x) va fi între valorile -3 și 3.

Cei 4 din interiorul funcției sinusoidale determină graficul funcției să sufere o compresie orizontală cu un factor de 1/4.

Pe de altă parte, perioada unei funcții este măsurată orizontal. Deoarece perioada funcției sin (x) este 2π, având în vedere sin (4x), dimensiunea perioadei se va schimba.

Pentru a afla care este perioada y = 3sen (4x), trebuie doar să multiplicați perioada funcției sin (x) cu 1/4 (factorul de compresie).

Cu alte cuvinte, perioada funcției y = 3sin (4x) este 2π / 4 = π / 2, așa cum se poate vedea în ultimul grafic.

Referințe

1. Fleming, W. și Varberg, D. E. (1989). Precalcul Matematică. Prentice Hall PTR.
2. Fleming, W. și Varberg, D. E. (1989). Matematica Precalcul: o abordare de rezolvare a problemelor (2, Ed. Ilustrată). Michigan: Prentice Hall.
3. Larson, R. (2010). Precalcul (8 ed.). Cengage Learning.
4. Pérez, C. D. (2006). Precalcul. Pearson Education.
5. Purcell, E. J., Varberg, D. și Rigdon, S. E. (2007). Calcul (Ediția a noua). Prentice hall.
6. Saenz, J. (2005). Calcul diferențial cu funcții transcendente timpurii pentru Știință și Inginerie (Ediția a II-a ed.). Ipotenuză.
7. Sullivan, M. (1997). Precalcul. Pearson Education.