Care sunt părțile planului cartezian?

părți ale planului cartezian Sunt compuse din două linii reale, perpendiculare, care împart planul cartezian în patru regiuni. Fiecare dintre aceste regiuni se numește cadrane și elementele planului cartezian se numesc puncte. Planul, împreună cu axele de coordonate, se numește Avion cartezian în cinstea filosofului francez René Descartes, care a inventat geometria analitică.

Cele două linii (sau axe de coordonate) sunt perpendiculare deoarece formează un unghi de 90º între ele și se intersectează într-un punct comun (origine). Una dintre linii este orizontală, fiind numită originea x (sau abscisă) iar cealaltă linie este verticală, fiind numită originea lui y (sau ordonată).

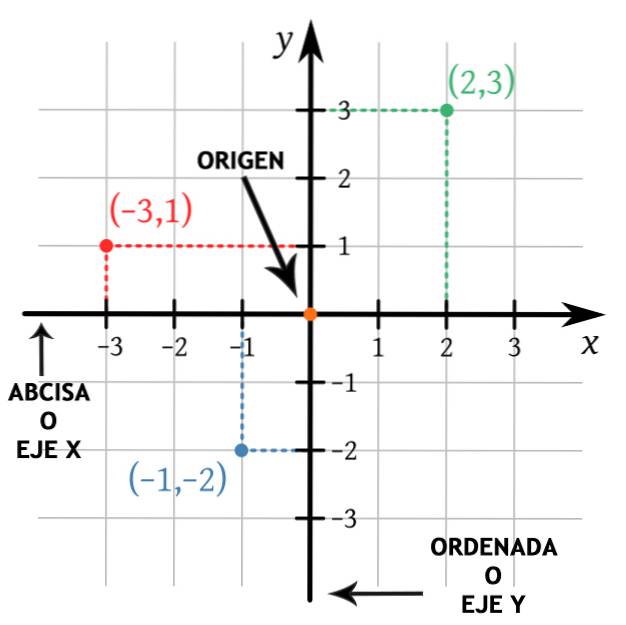
Jumătatea pozitivă a axei X este în dreapta originii, iar jumătatea pozitivă a axei Y este în sus față de origine. Acest lucru permite să se distingă cele patru cadrane ale planului cartezian, care este foarte util atunci când se trasează puncte în plan..

Punctele planului cartezian

În fiecare moment P planului i se poate atribui o pereche de numere reale care sunt coordonatele sale carteziene.

Dacă trec o linie orizontală și o linie verticală P, iar acestea intersectează axa X și axa Y în puncte la Da b respectiv coordonatele lui P Sunt (la,b). Se numeste (la,b) este importantă o pereche ordonată și ordinea în care sunt scrise numerele.

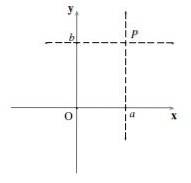
Primul număr, la, este coordonata din „x” (sau abscisă) și al doilea număr, b, este coordonata y (sau ordonată). Se utilizează notația P = (la,b).

Este evident din modul în care a fost construit planul cartezian că originea corespunde coordonatelor 0 pe axa "x" și 0 pe axa "y", adică, SAU= (0,0).

Cadranții planului cartezian

Așa cum se poate vedea în figurile anterioare, axele de coordonate generează patru regiuni diferite care sunt cadranele planului cartezian, care sunt notate cu literele I, II, III Da IV iar acestea se deosebesc unele de altele prin semnul posedat de punctele care se află în fiecare dintre ele.

Cuadrant Eu

Punctele cadranului Eu sunt cele care au ambele coordonate cu un semn pozitiv, adică coordonatele lor x și coordonata y sunt pozitive.

De exemplu, punctul P = (2,8). Pentru a-l grafica, punctul 2 este situat pe axa „x” și punctul 8 pe axa „y”, apoi se trasează respectiv liniile verticale și orizontale, iar unde se intersectează este locul unde se află punctul. P.

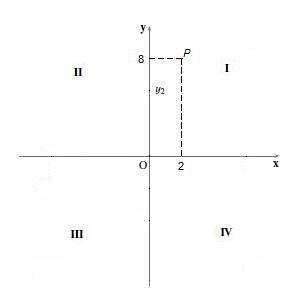
Cuadrant II

Punctele cadranului II au o coordonată „x” negativă și o coordonată „y” pozitivă. De exemplu, punctul Q = (- 4,5). Este reprezentat grafic procedând ca în cazul anterior.

Cuadrant III

În acest cadran semnul ambelor coordonate este negativ, adică coordonatele „x” și coordonatele „y” sunt negative. De exemplu, punctul R = (- 5, -2).

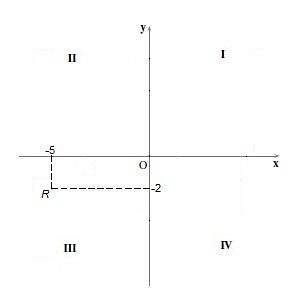
Cuadrant IV

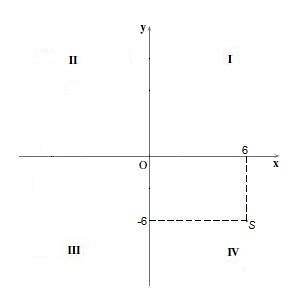
În cadran IV punctele au o coordonată „x” pozitivă și o coordonată „y” negativă. De exemplu punctul S = (6, -6).

Referințe

1. Fleming, W. și Varberg, D. (1991). Algebră și trigonometrie cu geometrie analitică. Pearson Education.
2. Larson, R. (2010). Precalcul (8 ed.). Cengage Learning.
3. Leal, J. M. și Viloria, N. G. (2005). Geometrie analitică plană. Mérida - Venezuela: Editorial Venezolana C. A.
4. Oteyza, E. (2005). Geometrie analitică (Ediția a doua). (G. T. Mendoza, Ed.) Pearson Education.
5. Oteyza, E. d., Osnaya, E. L., Garciadiego, C. H., Hoyo, A. M. și Flores, A. R. (2001). Geometrie analitică și trigonometrie (Prima ediție). Pearson Education.
6. Purcell, E. J., Varberg, D. și Rigdon, S. E. (2007). Calcul (Ediția a noua). Prentice hall.
7. Scott, C. A. (2009). Geometrie plană carteziană, parte: Conici analitice (1907) (ed. reimprimată). Sursa fulgerului.