
Derivată de calcul cotangent, dovadă, exerciții
derivat al cotangentei este egal cu opusul pătratului cosecantului "-CscDouă”. Această formulă respectă legile derivatei prin definiție și diferențierea funcțiilor trigonometrice. Se notează după cum urmează:
d (ctg u) = -cscDouă sau. du
În cazul în care „du” simbolizează expresia derivată din funcția argument, în raport cu variabila independentă.

Indice articol
- 1 Cum se calculează?
- 2 Caracteristicile funcției cotangente
- 2.1 Asimptote verticale
- 2.2 Domeniu
- 2.3 Gama
- 2.4 Frecvența
- 2.5 Comportament
- 3 Demo
- 3.1 Proba diferențială trigonometrică
- 3.2 Dovada prin definiția derivatului
- 4 exerciții rezolvate
- 4.1 Exercițiul 1
- 4.2 Exercițiul 2
- 5 Referințe
Cum se calculează?
Procedura de dezvoltare a acestor derivați este destul de simplă. Tot ce trebuie să faceți este să identificați corect argumentul și tipul de funcție pe care îl reprezintă..
De exemplu, expresia Ctg (f / g) are o diviziune în argumentul său. Acest lucru va necesita o diferențiere în ceea ce privește U / V, după dezvoltarea derivatei cotangentei.
Cotangenta este reciprocă a tangentei. Algebric acest lucru înseamnă că:
(1 / tg x) = ctg x
Ctg x = Cos x / Sen x
Este incorect să spunem că funcția cotangentă este „inversa” tangentei. Acest lucru se datorează faptului că funcția tangentă inversă prin definiție este tangentă arc.
(Tg-1 x) = arctg x
Conform trigonometriei pitagoreice, cotangenta este implicată în următoarele secțiuni:
Ctg x = (cos x) / (sin x)
CtgDouă x + 1 = CscDouă X
Conform trigonometriei analitice, acesta răspunde la următoarele identități:
Ctg (a + b) = (1 - tg a. Tg b) / (tg a + tg b)
Ctg (a - b) = (1 + tg a. Tg b) / (tg a - tg b)
Ctg (2a) = (1 - tgDouă a) / (2tg a)
Caracteristicile funcției cotangente
Este necesar să se analizeze diverse caracteristici ale funcției f (x) = ctg x pentru a defini aspectele necesare studierii diferențierii și aplicării acesteia.
Asimptote verticale
Funcția cotangentă nu este definită pe valorile care fac expresia „Senx” zero. Datorită echivalentului său Ctg x = (cos x) / (sin x), va avea o nedeterminare în toate „nπ” cu n aparținând numerelor întregi.
Adică, în fiecare dintre aceste valori ale x = nπ va exista o asimptotă verticală. Pe măsură ce vă apropiați din stânga, valoarea cotangentei va scădea rapid și, pe măsură ce vă apropiați din dreapta, funcția va crește la nesfârșit.
Domeniu
Domeniul funcției cotangente este exprimat prin mulțimea x ∈ R / x ≠ nπ, n ∈ Z. Aceasta se citește ca „x aparținând setului de numere reale astfel încât x este diferit de nπ, cu n aparținând setului de numere întregi”.
Rang
Gama funcției cotangente este de la minus la plus infinit. Prin urmare, se poate concluziona că domeniul său este ansamblul numerelor reale R.
Frecvență
Funcția cotangentă este periodică și perioada sa este egală cu π. În acest fel, egalitatea Ctg x = Ctg (x + nπ) este îndeplinită, unde n aparține lui Z.
Comportament
Este o funcție ciudată, deoarece Ctg (-x) = - Ctg x. În acest fel se știe că funcția prezintă o simetrie față de originea coordonatelor. De asemenea, prezintă o scădere a fiecărui interval situat între 2 asimptote verticale succesive.
Nu are valori maxime sau minime, deoarece aproximările sale la asimptotele verticale prezintă comportamente în care funcția crește sau scade la infinit.
Zerourile sau rădăcinile funcției cotangente se găsesc la multipli impar de π / 2. Aceasta înseamnă că Ctg x = 0 este valabil pentru valorile formei x = nπ / 2 cu n număr întreg impar.
Demonstrație
Există 2 moduri de a demonstra derivata funcției cotangente.
Dovada diferențială trigonometrică
Se demonstrează derivata funcției cotangente din echivalentul său în sinusuri și cosinus.
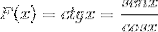
Este tratat ca derivatul unei diviziuni de funcții
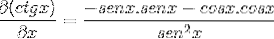
După derivare, factorii sunt grupați și scopul este de a emula identitățile pitagoreice
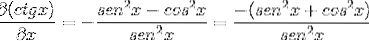
Înlocuind identitățile și aplicând reciprocitatea, se obține expresia
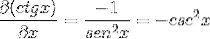
Dovadă prin definiția derivatului
Următoarea expresie corespunde derivatului prin definiție. În cazul în care distanța dintre 2 puncte ale funcției se apropie de zero.
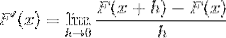
Înlocuind cotangenta avem:
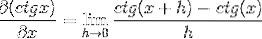
Identitățile sunt aplicate pentru suma argumentelor și reciprocitate
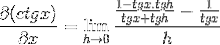
Fracția numărătorului este operată în mod tradițional
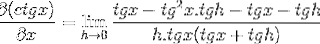
Eliminând elementele opuse și luând un factor comun, obținem
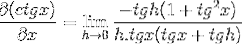
Aplicarea identităților și a reciprocității pitagoreice trebuie să o facem
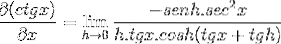
Elementele evaluate în x sunt constante în raport cu limita, prin urmare pot lăsa argumentul acestei. Apoi se aplică proprietățile limitelor trigonometrice.
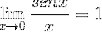
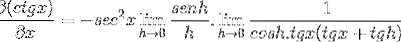
Limita este evaluată
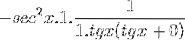
Apoi, se ia în calcul până se atinge valoarea dorită
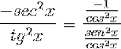
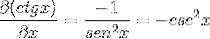
Derivata cotangentei este astfel demonstrată ca opusul pătratului cosecantei.
Exerciții rezolvate
Exercitiul 1
Pe baza funcției f (x), definiți expresia f '(x)
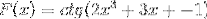
Derivația corespunzătoare se aplică respectând regula lanțului
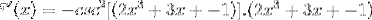
Derivarea argumentului
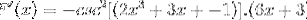
Uneori este necesar să se aplice identități reciproce sau trigonometrice pentru a adapta soluțiile.
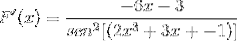
Exercițiul 2
Definiți expresia diferențială corespunzătoare lui F (x)
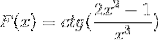
Conform formulei de derivare și respectând regula lanțului
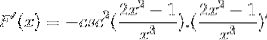
Argumentul este derivat, în timp ce restul rămâne același
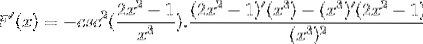
Derivând toate elementele
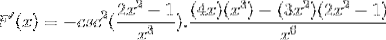
Operând într-un mod tradițional produsele din aceeași bază
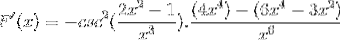
Se adaugă elemente egale și se extrage factorul comun
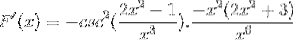
Semnele sunt simplificate și operate. Dând cale expresiei pe deplin derivate
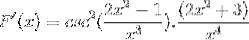
Referințe
- Seria trigonometrică, volumul 1. A. Zygmund. Cambridge University Press, 2002
- Calculul unei singure variabile. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 noiembrie 2008
- Calcul cu trigonometrie și geometrie analitică. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Editori săsești, 1988
- Analiza multivariabilă. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 dec. 2010
- Dinamica sistemelor: modelarea, simularea și controlul sistemelor mecatronice. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mar 2012
- Calcul: matematică și modelare. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 ianuarie 1999


Nimeni nu a comentat acest articol încă.