
Derivate implicite cum sunt rezolvate și exerciții rezolvate
derivate implicite Sunt instrumente utilizate într-o tehnică de diferențiere aplicată funcțiilor. Acestea sunt aplicate atunci când nu este posibil, în cadrul metodelor obișnuite, să se șteargă variabila dependentă care trebuie derivată. Această degajare se realizează pe baza variabilei independente.
De exemplu, în expresia 3xy3 - 2y + xyDouă = xy, nu puteți obține expresia care definește „y” ca funcție a „x”. Astfel încât prin derivarea expresiei diferențiale se poate obține dy / dx.

Indice articol
- 1 Cum se rezolvă derivatele implicite??
- 2 Regula lanțului
- 3 Ordinea operațională
- 4 Implicit al unei funcții
- 5 Istorie
- 6 Aplicații
- 7 exerciții rezolvate
- 7.1 Exercițiul 1
- 7.2 Exercițiul 2
- 8 Referințe
Cum sunt rezolvate derivatele implicite?
Pentru a rezolva o derivată implicită, începem cu o expresie implicită. De exemplu: 3xy3 - 2y + xyDouă - xy = 0. Acest lucru a fost deja rezolvat corect, totuși acest lucru nu este o condiție necesară pentru a obține derivata lui y față de x. Apoi, fiecare dintre elemente este derivat respectând regula lanțului pentru funcții mixte:
3xy3 este compus din 2 variabile, deci d (3xy3) va fi tratat ca derivatul unui produs de funcții.
d (3xy3) / dx = 3y3 + 3yDouă.(3x) y '= 3y3 + 9xyDouă Y '
În cazul în care elementul y 'este cunoscut ca „și văr”Y reprezintă dy / dx
-2y Se derivă conform legii K.U = K.U '
d (-2y) = -2 y '
X yDouă presupune un alt diferențial compus dintr-un produs de funcții
d (xyDouă) = șiDouă + 2xy și '
-x și este tratat omolog
d (-xy) = -y - x y '
Acestea sunt substituite în egalitate, știind că derivata zero este zero.
3y3 + 9xyDouă y '- 2 y' + yDouă + 2xy y '- y - x y' = 0
Elementele care au termenul y 'sunt grupate pe o parte a egalității
3y3 + DaDouă - y = -9xyDouă y '+ 2 y' + x y '
Factorul comun y 'este extras în partea dreaptă a egalității
3y3 + DaDouă - y = y '(-9xyDouă + x + 2)
În cele din urmă, termenul care înmulțește y 'este eliminat. Astfel, se obține expresia corespunzătoare derivatei implicite a lui y față de x.
y '= dy / dx = (3y3 + DaDouă - y) / (- 9xyDouă + x + 2)
Regula lanțului
În derivarea implicită regula lanțului este întotdeauna respectată. Toate expresiile diferențiale vor fi date ca o funcție a variabilei independente X. Deci, fiecare variabilă θ alta decât X, trebuie să includă termenul dθ / dx după ce a fost derivată.
Acest termen va apărea numai în gradul I sau cu un exponent egal cu 1. Această calitate îl face complet clar în cadrul metodelor tradiționale de factoring. Astfel, este posibil să se obțină expresia care definește diferențialul dθ / dx.
Regula lanțului arată natura progresivă a diferențierii sau a procesului derivat. Unde pentru fiecare funcție compusă f [g (x)], avem că expresia diferențială a lui f va fi
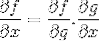
Ordinea operațională
În fiecare formulă sau lege de derivare aplicată, trebuie luată în considerare ordinea variabilelor între ele. Criteriile asociate variabilei independente sunt respectate, fără a modifica corelația acesteia cu variabila dependentă..
Relația variabilei dependente la momentul derivării este luată direct; cu excepția faptului că aceasta va fi considerată a doua funcție, motiv pentru care criteriul regulii lanțului este aplicat pentru funcțiile mixte.
Acest lucru poate fi dezvoltat în expresii cu mai mult de 2 variabile. Conform acelorași principii, vor fi notate toate diferențialele referitoare la variabilele dependente.
Grafic, se tratează același criteriu care definește derivata. În timp ce derivata este panta liniei tangente la curba în plan, restul diferențialelor aparținând variabilelor dependente (dy / dx, dz / dx) reprezintă planuri tangente corpurilor vectoriale descrise de funcțiile variabilei multiple.
Implicit a unei funcții
Se spune că o funcție este definită implicit, dacă expresia y = f (x) poate fi reprezentată ca o funcție variabilă multiplă F (x, y) = 0 atâta timp cât F este definit în planul RDouă.
3xy3 - 2y + xyDouă = xy poate fi scris sub forma 3xy3 - 2y + xyDouă - xy = 0
Având în vedere imposibilitatea explicitării funcției y = f (x).
Poveste
Calculul diferențial a început să fie numit de diverși cercetători matematici în jurul secolului al XVII-lea. Prima dată a fost menționată prin contribuțiile lui Newton și Leibniz. Ambele au tratat calculul diferențial din diferite puncte de vedere, dar convergând în rezultatele lor.
În timp ce Newton s-a concentrat pe diferențiere ca viteză sau ritm de schimbare, abordarea lui Leibniz a fost mai geometrică. Se poate spune că Newton a atacat presupunerile lăsate de Apollonius de Perge și Leibniz ideile geometrice ale lui Fermat.
Derivarea implicită apare imediat când se iau în calcul ecuațiile diferențiale și integrale. Acestea au extins conceptul geometric al lui Leibniz la R3 și chiar spații multidimensionale.
Aplicații
Derivatele implicite sunt utilizate în diverse situații. Acestea sunt frecvente în problemele ratei de schimb între variabilele conexe, unde, în funcție de sensul studiului, variabilele vor fi considerate dependente sau independente..
Au, de asemenea, aplicații geometrice interesante, cum ar fi în probleme de reflecție sau umbră, pe figuri a căror formă poate fi modelată matematic..
Sunt frecvent utilizate în domeniile economiei și ingineriei, precum și în diverse investigații ale fenomenelor naturale și clădirilor experimentale..
Exerciții rezolvate
Exercitiul 1
Definiți expresia implicită care definește dy / dx
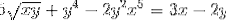
Fiecare element al expresiei este diferențiat
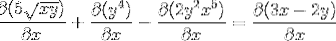
Stabilirea regulii lanțului în fiecare caz competent
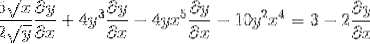
Gruparea pe o parte a egalității a elementelor care au dy / dx
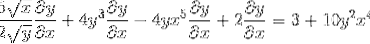
Se ia în considerare folosind factorul comun
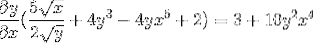
Se rezolvă obținând expresia căutată
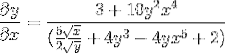
Exercițiul 2
Definiți expresia implicită care definește dy / dx
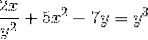
Exprimarea instrumentelor derivate care trebuie efectuate
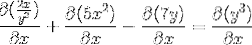
Derivând implicit conform regulii lanțului
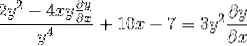
Factorizarea elementelor comune
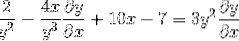
Gruparea termenului dy / dx pe o parte a egalității
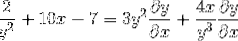
Factor comun elementului diferențial
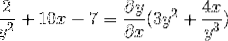
Izolăm și obținem expresia căutată
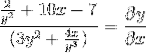
Referințe
- Calculul unei singure variabile. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 noiembrie 2008
- Teorema funcției implicite: istorie, teorie și aplicații. Steven G. Krantz, Harold R. Parks. Springer Science & Business Media, 9 noiembrie. 2012
- Analiza multivariabilă. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 dec. 2010
- Dinamica sistemelor: modelarea, simularea și controlul sistemelor mecatronice. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mar 2012
- Calcul: matematică și modelare. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 ianuarie 1999



Nimeni nu a comentat acest articol încă.